小4算数「分数」指導アイデア《帯分数を仮分数に直す方法を考える》
執筆/東京都渋谷区立猿楽小学校教諭・田中大樹
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、東京都板橋区立上板橋小学校副校長・内藤信義
目次
年間指導計画
・大きい数
・折れ線グラフ
・角とその大きさ
・わり算1桁
・小数のしくみ
・垂直・平行と四角形
・わり算2桁
・およその数、計算の見積もり
・そろばん
・倍の見方
・資料の整理
・式と計算
・変わり方
・面積
・分数
・小数のかけ算とわり算
・直方体と立方体
単元の展開(各時の主な学習活動内容)
第1時 真分数・仮分数・帯分数の表し方や意味を理解する。
第2時 数直線や単位分数に着目し、仮分数や帯分数で表す。
第3時 仮分数を帯分数に直す方法を考える。
第4時(本時)帯分数を仮分数に直す方法を考える。
第5時 異分母分数の大小関係について考える。
第6時 同分母の分数のたし算・ひき算の仕方を考える。同分母の「真分数+真分数(繰り上がりあり)」、同分母の「仮分数-真分数」
第7時 同分母の帯分数のたし算の仕方を考える。同分母の「帯分数+帯分数(繰り上がりなし)」、同分母の「帯分数+帯分数、帯分数+真分数(繰り上がりあり)」
第8時 同分母の帯分数のひき算の仕方を考える。同分母の「帯分数-帯分数、帯分数-真分数(繰り下がりあり)」
本時のねらい
数直線や単位分数を基にして、帯分数を仮分数に直す方法を理解する。
評価規準
単位分数のいくつ分かという考えを基に、帯分数を仮分数に直すことができる。
本時の教材のポイント
本時では、帯分数を仮分数に直す方法を考えます。その際、前時の仮分数を帯分数に直す際に考えた以下のような学習経験が本時の問題を考える際のポイントになります。
・仮分数と帯分数の両方を数直線に表して考えたこと
・1=[MATH]\(\frac{□}{□}\)[/MATH]であることを基に仮分数の中に整数がいくつあるか考えたこと
・単位分数がいくつ分かに着目して、計算をして考えたこと
この学習経験を生かし、数直線に表して帯分数である2[MATH]\(\frac{2}{3}\)[/MATH]と仮分数である[MATH]\(\frac{8}{3}\)[/MATH]が同じ値であることを捉えたり、帯分数の整数の部分に着目して仮分数で表したり、仮分数で表した際の分子の数は「単位分数がいくつ分か」を表していると考えたりしていきます。そして、最終的には、2[MATH]\(\frac{2}{3}\)[/MATH]を仮分数に直す際に、分子の大きさを3×2+2=8と計算して[MATH]\(\frac{8}{3}\)[/MATH]と考えます。その際、この計算で求めた8が「単位分数がいくつ分か」を表していることを、数直線と対応させながら確認していくことが大切です。
分数の学習において、大きさを捉え、数直線などに表すことが苦手な子供が見られます。これは1としている部分と、それを□等分した1つ分が単位分数になっているという理解が不十分であることが考えられます。数直線などで分数の大きさを表すときには、まず1の大きさを決め、その1を何等分するか考え、その1目盛りが単位分数になるということを押さえることが重要です。その上で、数直線を基に、1は[MATH]\(\frac{1}{3}\)[/MATH]が3つなので[MATH]\(\frac{3}{3}\)[/MATH]、2は[MATH]\(\frac{1}{3}\)[/MATH]が6つなので[MATH]\(\frac{6}{3}\)[/MATH]であることを確認し、2[MATH]\(\frac{2}{3}\)[/MATH]を仮分数で表すとどのような大きさになるのか調べていくことが大切です。
本時の展開
(前時で[MATH]\(\frac{9}{4}\)[/MATH]を2[MATH]\(\frac{1}{4}\)[/MATH]に直したことをふり返りながら)前の時間では、仮分数を帯分数に直す方法を考えました。どのように考えましたか。
仮分数の中に1([MATH]\(\frac{4}{4}\)[/MATH])がいくつあるか考えました。
数直線に表して考えました。
[MATH]\(\frac{1}{4}\)[/MATH]がいくつ分かで考えました。分子の数を分母の数で割って、商が整数の部分、余りが分数の部分になりました。
そうでしたね。今日はその逆のことを考えます。帯分数を仮分数に直すには、どうすればよいでしょうか。

2[MATH]\(\frac{2}{3}\)[/MATH]を仮分数に直そう。
2[MATH]\(\frac{2}{3}\)[/MATH]を仮分数に直すには、どんな方法があるでしょうか。
前の時間のように数直線に表してみると分かりやすいと思います。
前にやったことの逆をすればいいと思います。
今度は整数の2を分数に直せばいいのかな。
仮分数を帯分数に直したときのやり方が使えないかなというのはよい視点です。では、どんな方法があるか、自分なりに考えてみましょう。

帯分数を仮分数に直す方法を考えよう。
見通し
数直線に表して考えてみよう。
2[MATH]\(\frac{2}{3}\)[/MATH]の整数の2を分数に直してみよう。
[MATH]\(\frac{1}{3}\)[/MATH]がいくつあるかを考えてみよう。
自力解決の様子
A つまずいている子
・整数の部分を仮分数で表すことができない。
・正しく数直線に表すことができない。
B 素朴に解いている子
・数直線に表して、2[MATH]\(\frac{2}{3}\)[/MATH]と[MATH]\(\frac{8}{3}\)[/MATH]が同じ大きさであると考えている。
C ねらい通り解いている子
・2[MATH]\(\frac{2}{3}\)[/MATH]を整数と分数に分け、1=[MATH]\(\frac{3}{3}\)[/MATH]、2は[MATH]\(\frac{3}{3}\)[/MATH]が2つだから[MATH]\(\frac{6}{3}\)[/MATH]と考え、[MATH]\(\frac{2}{3}\)[/MATH]と合わせて[MATH]\(\frac{8}{3}\)[/MATH]としている。
・2[MATH]\(\frac{2}{3}\)[/MATH]の中に[MATH]\(\frac{1}{3}\)[/MATH]がいくつあるかに着目し、3×2+2=8と計算して[MATH]\(\frac{1}{3}\)[/MATH]が8個あるから、[MATH]\(\frac{8}{3}\)[/MATH]と考えている。
全体発表とそれぞれの考えの関連付け
それでは、考えを発表してもらいましょう。
前の時間にやったように数直線に書いてみました。そうしたら、2[MATH]\(\frac{2}{3}\)[/MATH]のところは、[MATH]\(\frac{8}{3}\)[/MATH]になったので、2[MATH]\(\frac{2}{3}\)[/MATH]を仮分数に直すと[MATH]\(\frac{8}{3}\)[/MATH]になります。
数直線に書いてみたのですね。黒板にも数直線を書いてみんなで確認してみましょう。まず、1はここだとすると0と1の間には、どのように目盛りを書きますか。

分母が3だから、1を3等分します。

この目盛り1つ分の大きさはいくつですか。
1を3等分した1つ分だからここは[MATH]\(\frac{1}{3}\)[/MATH]です。
なるほど。では1目盛りの大きさが[MATH]\(\frac{1}{3}\)[/MATH]になるように、この先に目盛りを入れていきます。この数直線の目盛りにみんなで数を書いてみましょう。

※書き込む(1人で全部書かせずに交代しながら数値を書かせていくとよいです)。
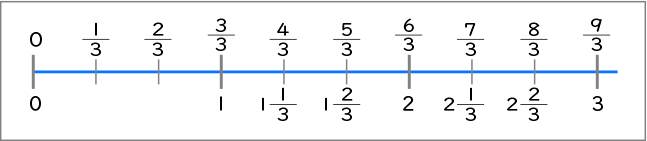
確かに、2[MATH]\(\frac{2}{3}\)[/MATH]のところに[MATH]\(\frac{8}{3}\)[/MATH]がありますね。数直線を使うとどんなことが分かりやすくなりましたか。
分数の大きさが分かりやすくなりました。
目盛りを数えると分かりやすいです。
他の帯分数と仮分数の関係も分かりやすくなりました。
他の考えの人はいますか。
整数の部分を分数に変えてみました。1を分数にすると[MATH]\(\frac{3}{3}\)[/MATH]です。整数の部分の2は[MATH]\(\frac{3}{3}\)[/MATH]が2つ分で[MATH]\(\frac{6}{3}\)[/MATH]だから、そこに分数の部分の[MATH]\(\frac{2}{3}\)[/MATH]を合わせて[MATH]\(\frac{8}{3}\)[/MATH]になりました。
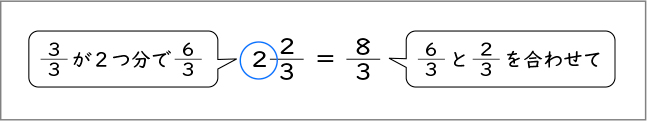
なるほど。整数の部分を分数に直して、分数の部分と合わせる方法ですね。
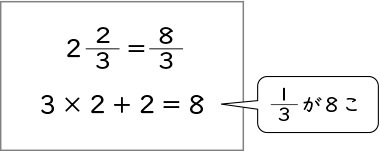
私は[MATH]\(\frac{1}{3}\)[/MATH]がいくつあるかを考えて、3×2+2=8と計算しました。[MATH]\(\frac{1}{3}\)[/MATH]が8個なので[MATH]\(\frac{8}{3}\)[/MATH]と考えました。

計算で考えたのですね。3×2や+2は何を表していますか。
1は[MATH]\(\frac{1}{3}\)[/MATH]が3個で、整数の部分は2だから、3×2=6で[MATH]\(\frac{1}{3}\)[/MATH]が6個ということで、分数の部分は[MATH]\(\frac{1}{3}\)[/MATH]が2個なので、+2しています。
数直線の1目盛りは[MATH]\(\frac{1}{3}\)[/MATH]です。その[MATH]\(\frac{1}{3}\)[/MATH]の目盛りがいくつあるかを考えていると思います。
[MATH]\(\frac{1}{3}\)[/MATH]がいくつあるかを考えると、2のところまでで3×2=6つ、2からは目盛り2つ分あります。全部で8つあるので[MATH]\(\frac{8}{3}\)[/MATH]になります。

3×2+2は、[MATH]\(\frac{1}{3}\)[/MATH]がいくつあるかを考えた式なのですね。帯分数を仮分数に直すために、前の時間に考えたこともうまく使っていろいろな方法を考えることができました。
ふり返り
今日の学習をふり返ってみましょう。どんなことが分かりましたか。
数直線に表すと仮分数と帯分数の関係がよく分かりました。
帯分数は、整数の部分を分数にして分数の部分と合わせると仮分数になることが分かりました。
[MATH]\(\frac{1}{3}\)[/MATH]がいくつ分かを考えると仮分数で表せました。分子の数は計算で求めることができました。
これからも仮分数を帯分数に直したり、帯分数を仮分数に直したりする場面があります。仮分数と帯分数それぞれのよさにも目を向けながら、どちらも使いこなせるようにしていきましょう。
まとめ
帯分数は、整数の部分に着目して[MATH]\(\frac{1}{3}\)[/MATH]がいくつ分かを考えると仮分数に直せる。
評価問題
次の帯分数を仮分数に直しましょう。
①1[MATH]\(\frac{3}{5}\)[/MATH] ②3[MATH]\(\frac{2}{3}\)[/MATH] ③2[MATH]\(\frac{4}{7}\)[/MATH]
子供に期待する解答の具体例
①5×1+3=8 [MATH]\(\frac{8}{5}\)[/MATH]
②3×3+2=11 [MATH]\(\frac{11}{3}\)[/MATH]
③7×2+4=18 [MATH]\(\frac{18}{7}\)[/MATH]
ポイント&アドバイス
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

