小4算数「2桁で割るわり算」指導アイデア《筆算で過大商を立てたときの仮商修正の仕方を理解して計算する》
執筆/渋谷区立渋谷本町学園主幹教諭・鈴木博之
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、板橋区立上板橋小学校副校長・内藤信義
目次
年間指導計画
・大きい数
・折れ線グラフ
・角とその大きさ
・わり算1桁
・小数のしくみ
・垂直・平行と四角形
・わり算2桁
・およその数、計算の見積もり
・そろばん
・倍の見方
・資料の整理
・式と計算
・変わり方
・面積
・分数
・小数のかけ算とわり算
・直方体と立方体
単元の展開(各時の主な学習活動内容)
第1時 数の構成に着目し、「何十で割る計算」の仕方を考える。
第2時 「2位数÷2位数(仮商修正なし、余りなし)」の筆算の仕方を考え理解する。
第3時 「2位数÷2位数(仮商修正なし、余りあり)」の筆算の仕方を考え理解する。また、「割る数×商+余り=割られる数」の関係と検算の仕方を理解する。
第4時(本時) 「2位数÷2位数」の筆算で、過大商を立てたときの仮商修正の仕方を考え、その計算をする。
第5時 「2位数÷2位数」の筆算で、過小商を立てたときの仮商修正の仕方を考え、その計算をする。
第6時 「2位数÷2位数」の筆算で、除数の切り捨てや切り上げを選んで仮商を立てて計算する。
第7時 「2位数÷2位数」の筆算を基に「3位数÷2位数=1位数」の筆算の仕方を考え、その計算をする。
第8時 「3位数÷2位数=2位数」の筆算の仕方を考え、その計算をする。
第9時 「3位数÷2位数=2位数」の筆算で、除数の切り捨てや切り上げを選んで仮商を立てて計算する。
第10時 商に0が立つ場合の簡便な筆算の仕方や「3位数÷3位数」の筆算の仕方を考え、その計算をする。
第11時 除法について成り立つ性質を考え、理解する。
第12時 末尾に0のある数の除法の簡便な筆算の仕方と余りの求め方を考え、その計算をする。
第13時 割られる数や割る数の一部が分かっていない場合のわり算の筆算(虫食い算)について、筆算の仕組みを考えながら解決する。
第14時 学習内容の定着を確認し、理解を確実にする。
本時のねらい
2位数÷2位数の筆算で、過大商を立てたときの仮商修正の仕方を理解し、その計算ができる。
評価規準
商の見当を用いて仮商をたて、過大商のときの仮商を修正し、計算することができる。
本時の教材のポイント
本時では、2位数÷2位数の計算において、10のまとまりを意識して仮商を立てたときに、仮商が大き過ぎて修正する必要がある場合の筆算の仕方について学習します。
本単元では、第1時に何十÷何十の計算の仕方を学習しました。何十÷何十の計算では、10のまとまりを単位として数を捉えることで、既習である除数が一位数の除法を用いて計算できることを学習します。そして、除数が何十ではない2位数÷2位数の計算において、第1時で学習した計算を活用し、除数や被除数を何十と見ることで、商の見当を付けて計算をします。例えば、84÷21のような計算は、80÷20と見ることで商が4になると見当を付けます。
本時では、前時までのように除数の一の位を切り捨てて、何十で割る計算と捉えて商の見当を付けた際に、仮商が大き過ぎて修正が必要となる問題を扱います。具体的には、94÷33などの問題を扱い、除数を30として商の見当を付け、仮商の3を小さく修正して正しい商を求めます。仮商の値を小さく修正することについて考える際には、筆算の各手順や余りの意味などを確認しながら、なぜ商の修正をする必要があるのか、どのように修正したらよいのかということを、子供が捉えられるように進めていくことがポイントとなります。そのため、本時では、あえて解決の途中の段階にある考えを取り上げ、解決すべき視点を明確にしていきます。
また、導入で前時までに学習した仮商の修正がない筆算を扱い、既習を確認した上で、仮商の修正がある問題を扱います。これらの計算の共通点や相違点に目を向けることを通して、2桁÷2桁の計算について理解を深めることができるようにしました。
本時の展開
昨日までどんな学習をしていましたか。
2桁のわり算の筆算です。
そうでしたね。では、94÷31を筆算で計算してみましょう。できた人は、商をどうやって考えたのかもノートに書きましょう。
では、黒板に書いて説明してください。
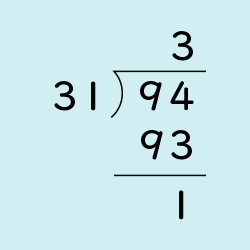
商に3を立てて、31×3=93、94-93=1なので、3あまり1です。
商はどうして3だと思ったのですか。
9÷3=3だからです。
94÷31はだいたい90÷30です。90と30を 計算しやすいように 10のまとまりで考えて、9÷3をしました。
十の位の数が9と3だから、一の位の数を切り捨てて9÷3にして、商を3にしました。
なるほど。94÷31を90÷30と見て、商の見当を付けたのですね。今日はこのようにいろいろなわり算の筆算の仕方を説明しましょう。まずは、94÷33の筆算について考えてみましょう。

筆算の仕方を説明しましょう。
見通し
まずは筆算を書いて計算してみましょう。
90÷30を基に商を考えてみよう。
90÷30=3だけど、商が本当に3でよいのか考えてみよう。
33×□が割られる数の96を超えないように□を考えよう。
あれ? 3だと大きいかな。
ああ、そういうことか。できた!
手が止まっている人と、答えが出せている人がいるようですね。何かに気付いた人もいるようです。気付いたことがある人はノートに書いておきましょう。困っている人も、何に困っているかノートに書いておきましょう。
自力解決の様子
A つまずいている子
・仮商として3を立てている。仮商と除数の積が、被除数より大きくなりすぎて、ひき算ができないため、途中で解決が止まっている。
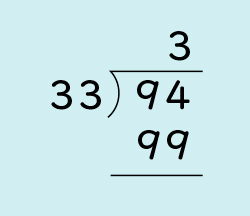
B 素朴に解いている子
・仮商として3を立てたが、仮商と除数の積が被除数より大きくなってしまうことに気付き、商を修正して正しく筆算をしている。
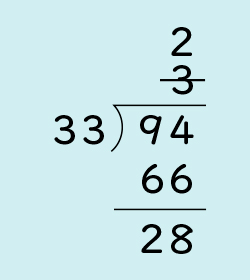
C ねらい通り解いている子
・適切な商を立てて、正しく筆算をしている。
・仮商を修正する方法や理由、筆算の手順について説明をしている。
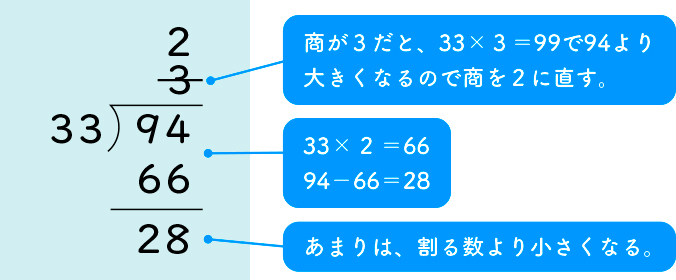
全体発表とそれぞれの考えの関連付け
何人かの人が、ノートにこのように書いていました。
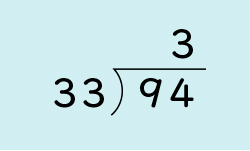
この人の気持ちが分かりますか。この人はどうやって考えたのでしょうか。
分かります。94÷33を90÷30に見立てて、3を立てたのだと思います。
見立ててというのは、とてもいい言葉ですね。このまま続けるとどうなりますか。
そのあとは、33×3=99をします。
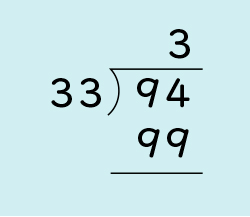
ここまでやって困っている人がいたのだけど、どんな気持ちか分かりますか。隣の人と話してみましょう。
※子供たちがペアで話をする。
どんな話をしましたか。
上が小さくて、下が大きいから引けなくて困っていると思います。
94-99ができなくて、どうしたらいいのか困っていると思います。
ひき算ができなくて困ったのですね。これはできない問題だったようですね。 問題が悪かったのでしょうか。
できます。
どうすればよいのですか。
3をやめて、商を2にすればよいです。見当を付けた商を1つ減らせばできます。
見当は予想だから、間違っていたら変えても大丈夫です。
見当を付けた商を変えてみるのですね。それで計算することができますか。
商が2だったら、33×2=66で、94より小さくなって引けるから、商を2にします。94-66=28だから、割る数よりあまりが大きくないから、商は2で合っています。
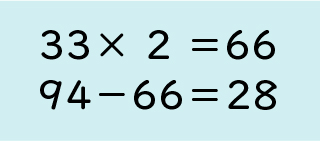
商が2だとできるということだけど、さっきの引けなくて困った問題は解決できそうですか。
できます。94-66=28だから引けるので、あまりは28になります。
今、話し合ったことを、筆算を書いて確認してみましょう。
はじめ、商は3だと思ったけれど、3だと大き過ぎるから、1つ減らして2にしました。33×2になります。ひき算をすると94-66=28です。あまりは割る数より小さくないといけないけれど、28なら33より小さくなります。
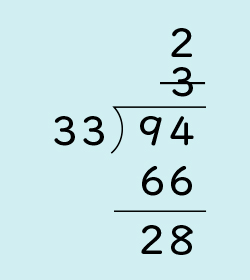
思っていたよりも、あまりがたくさん出ました。
こんなにあまりが大きくてもよいのですか。
33より小さければいいです。
33より大きいとだめです。33や34などだと、まだ割る数の33が引けるから商が変わります。
この問題は、初めにやった問題と比べて同じところは何ですか。
商を立てて、かけ算をして、引いて、あまりを出したことが同じでした。
初めの問題とどこか変わりましたか。
これまでのように商の見当を付けたら大きくて引けなかったです。
商が3だと3×33が94から引けなかったので商を小さくしました。
この問題は、はじめ見当を付けた商が合っていませんでした。間違っている商だと、3×33が94から引けなかったので商を小さくしました。
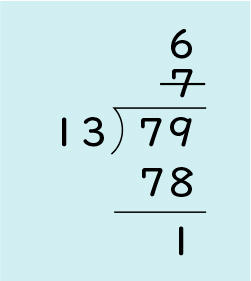
見当を付けた商を直すところがポイントでしたね。他の計算もやってみましょう。93÷32と79÷13を筆算で計算して説明しましょう。
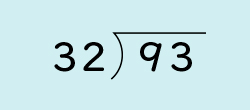
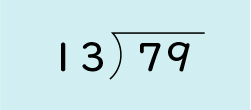
どのように解いたか説明してください。
90÷30を基にして商を考えると3になります。32×3=96なので、93-96が引けなくなってしまいます。だから商を2にして、32×2=64 をしました。93-64=29なので、答えは2あまり29です。
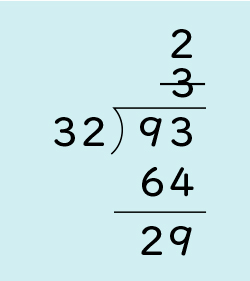
説明がとても上手でしたね。次の問題は、今のように、みんなも隣の人に説明してみましょう。
※ペアで説明し合う。
はじめに見当を付けた商を、仮の商と言います。仮の商が間違っていたときにはどうしましたか。
大き過ぎたときには、1つ小さい数に直しました。
もう少し違う数値でも問題を解いてみて、今の解き方が使えるか確かめてみましょう。67÷16だったらどうでしょうか。
■4まで修正できずにとまっている子
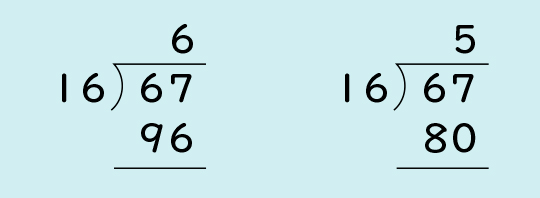
■4まで修正することに気付いている子
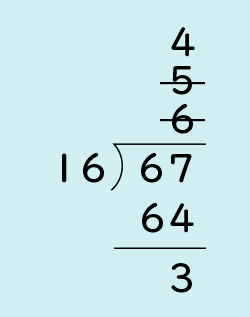
どのように考えたか説明してください。
60÷10で考えると、仮の商は6だけど、正しい商は6ではできませんでした。
5もだめです。4ならできました。
2回修正したらできました。
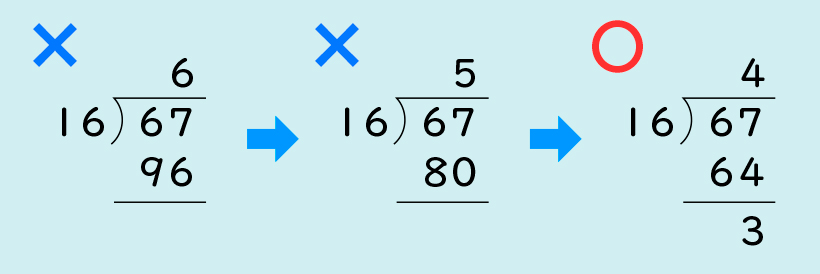
商を6にしたら、16×6=96で引けません。商を5にしても、16×5=80なのでだめです。商を4にしたら、16×4=64なので、67-64ができました。答えは4あまり3です。
この問題は、これまでの問題と比べてどうですか。同じところや違うところはありますか。
修正しているのは同じです。
2回も修正しました。
こんな風に2回修正する場合もあるのですね。もう1回修正して、商を3にしたらどうですか。16×3=48、67-48=19となります。
あまりが割る数の16より大きいからだめです。
割る数よりあまりが大きいとだめなのですね。
商の5は大き過ぎます。でも、3は小さ過ぎます。あまりが16より小さいので、商は4がちょうどいいです。
このちょうどいい商を見付けるには、どうしたらいいのでしょうか。
割られる数より小さくなるように、商を修正していきます。
あまりの大きさが割る数より小さくなるように修正します。
まとめ
・はじめに見当を付けた商を仮の商と言います。
・仮の商が大き過ぎたときには、あまりの大きさに気を付けて、商を小さく修正します。
ポイント&アドバイス
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

