小２算数「大きい数のたし算とひき算」指導アイデア《３位数－２位数の筆算の定着》
執筆／新潟大学附属新潟小学校教諭・二瓶亮
監修／東京都国立教育政策研究所教育課程調査官・加固希支男、新潟市立上所小学校教諭・志田倫明
目次
年間指導計画
・表とグラフ
・時刻と時間
・２けたのたし算
・２けたのひき算
・長さ
・1000までの数
・水のかさ
・大きい数のたし算とひき算
・三角形と四角形
・式と計算
・かけ算（１）
・かけ算（２）
・かけ算（３）
・1000より大きい数
・たし算とひき算の関係
・図を使って考えよう
・分けた大きさ
・箱の形
単元の展開（各時の主な学習活動内容）
第１時 ２位数＋２位数＝３位数（百の位への繰り上がりあり）の筆算の仕方
第２時 ２位数＋２位数＝３位数（十、百の位への繰り上がりあり）や２位数＋１・２位数＝３位数（百の位への波及的繰り上がりあり）の筆算の仕方
第３時 学習内容を適用して問題を解決する
第４時 ３位数－２位数（百の位からの繰り下がりあり）の筆算の仕方
第５時 ３位数－２位数（十、百の位からの繰り下がりあり）の筆算の仕方
第６時 ３位数－２位数（十、百の位からの波及的繰り下がりあり）の筆算の仕方
第７時（本時）３位数－２位数の筆算の定着を図る
第８時 ３位数＋１・２位数（百の位への繰り上がりあり）や３位数－１・２位数（百の位からの繰り下がりあり）の筆算の仕方
第９時 ３位数＋１・２位数（百の位への繰り上がりあり）や３位数－１・２位数（百の位からの繰り下がりあり）の筆算の仕方
第10時 学習内容の定着の確認及び数学的な見方・考え方のふり返り
本時のねらい
３位数－２位数の筆算の仕方とたしかめ算の方法について、定着を図るとともに理解を深める。
評価規準
繰り下がりが必要なことに気付き、正しく筆算の計算を行うことができる。
本時の教材のポイント
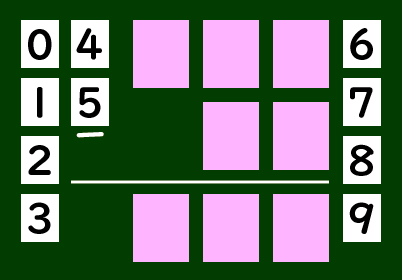
ここでは、第４〜６時までに学習した３位数－２位数の筆算の仕方をふり返るとともに、その定着を図ることを目的としています。そこで、本時では、３位数－２位数＝３位数となる筆算を、数字カードを当てはめて自分でつくる問題（本時の展開での図を参照）を提示し、同じ数字は２回使うことができないという条件を付け加えます。そうすることで、引かれる数と答えの百の位が異なる数にならないといけないことから、少なくとも百の位から十の位への繰り下がりが必要になります。つまり、この問題を解決するためのポイントは、百の位に着目して、同じ数字を使うことができないということに気付き、繰り下がりの必要性を見いだすことにあります。解決の見通しとして、その点を全体で共有します。
１回繰り下がりのある筆算をつくることができた子供には、２回繰り下がりのある筆算をつくることができるかチャレンジさせる声かけをしていきます。つくった筆算が合っているかを確かめることについても確認していくことが必要です。「先生、できたよ！」と見せに来る子供がいたときには、正しくつくることができているかを確かめる方法について問い、たしかめ算をするとよいことを全体に共有していきます。中には、たし算とひき算が逆の関係になっていることから、答えと引く数を足して引かれる数をつくり出そうとする子供もいるかもしれません。そういった気付きは、タイミングを見ながら全体に共有していくとよいでしょう。
本時の展開
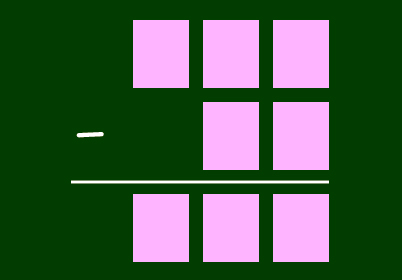
これまで、３桁－２桁の筆算を学習してきましたね。今日は、「穴埋め筆算ゲーム」をしようと思います。０〜９までの数字を当てはめて、正しい筆算の計算をつくりましょう。
※子供からゲームについての質問を受ける形で、ルールの確認をしていくことも考えられます。
楽しそう！ やってみたい！
四角は８個で数字は10個だね。
同じ数字は何回使ってもいいんですか。
同じ数字は２回使うことはできません。また、今回は必ず３桁－２桁＝３桁となるように筆算をつくってください。
ということは、①②③には、０を入れることはできないってことだね。
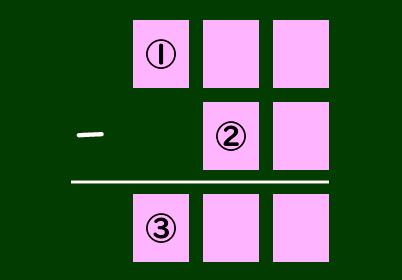
①②③に０が入ると、３桁や２桁じゃなくなってしまうもんね。
それでは、早速やってみましょう。
＜１人１台端末を活用した指導アイデア＞ あらかじめ筆算の枠と数字カードを１人１台端末で配信して、問題に取り組ませるとよいでしょう。その場合、数字カードを使うかどうかは子供に委ねてもよいでしょう。直接筆算の枠に書き込んだほうがやりやすいという子供に判断させるとよいでしょう。
３桁－２桁＝３桁となるように、四角に数字を入れて、正しい筆算の計算をつくろう。
※ただし、同じ数字は２回使えない。
見通し
まずは繰り下がりがない計算を考えてみよう。
百の位は差が１になるように数字が入るから、まず百の位に入る数を固定して考えていってみよう。
自力解決の様子
Ａ つまずいている子
・数字を当てはめてみるものの、繰り下がりが必要なことに気付くことができず、筆算を正しくつくることができない。
・引かれる数から引く数を引くのではなく、大きい数字から小さい数字を引いてしまい、正しく筆算の計算をつくることができていない。
Ｂ 素朴に解いている子
・数字を当てはめていく中で、引かれる数と答えの百の位が異なる数にならないといけないことに気付き、百の位から十の位への繰り下がりが必要なことを見いだしている。
Ｃ ねらい通り解いている子
・百の位に着目し、引かれる数と答えの百の位が異なる数にならないといけないことに気付き、百の位から十の位への繰り下がりが必要なことを見いだしている。
・３桁－２桁＝３桁になることから、引かれる数の百の位よりも答えの百の位が１小さくなることに気付いている。
全体発表とそれぞれの考えの関連付け
先生できました。これで合っているかな。
やっていて分かったんだけど、これは繰り下がりがないとできないんじゃないかな。
繰り下がりがないとできないのではないかと考えている人がいるみたいですが、みんなはどうでしたか。
繰り下がりは絶対必要です。
そうそう。だって引かれる数と答えの百の位が同じになっちゃダメでしょ。繰り下がりがないと、百の位に同じ数が入ってしまうから、百の位から十の位への繰り下がりが必要だよ。
例えば、419－62みたいに、百の位から十の位に１繰り下がることで、百の位が４から３になるでしょ。そうすれば、同じ数を使わなくてよくなるってこと。だから必ず１小さい数が答えの百の位には入るね。
なるほど。少なくとも、百の位から十の位への繰り下がりは絶対に必要だということですね。「この計算は合っているかな？」と心配していた人もいたのですが、確認する方法はありますか。
たしかめ算をすればいいです。前に習いました。
そうそう。答えと引く数を足して、引かれる数に戻ったら答えは正しい。戻らなかったら答えは間違っているっていう方法を学習したよね。数が大きくなっても同じだよ。
同じ数字を使っていないかのチェックも必要だよね。そっちのほうが先かもね。
そうでしたね。自分がつくった筆算が正しい計算になっているかを確かめる時間を取ります。たしかめ算をしてみましょう。
合っていました。ちゃんと引かれる数に戻った。
あれ？ 引かれる数に戻らない。どこが間違っているんだろう……。
あっ、分かった！ 一の位の７－８はできないのに、８－７として計算してしまっていたんだ。ということは、７と８の位置を入れ替えれば正しい計算にできそうだ。
たしかめ算をして、つくった筆算が正しく計算できているかを確認することが大切ですね。それでは、もう少し活動の時間を取るので、他の筆算もつくってみましょう。ちなみに、前に授業でやった２回繰り下がりにチャレンジしている人もいました。残った時間で、ぜひチャレンジしてみてください。
２回繰り下がるってことは、十の位から一の位への繰り下がりも必要になるってことだよね。難しそうだけどチャレンジしてみよう。
３位数－２位数（十、百の位からの繰り下がりあり）の筆算
３位数－２位数（十、百の位からの波及的繰り下がりあり）の筆算
まとめ
・同じ数字を２回使わずに、３桁－２桁＝３桁の筆算をつくるためには、少なくとも百の位から十の位への繰り下がりが必要。
・数が大きくなってもたしかめ算を使うことで、正しく計算できているかと確かめることができる。
ポイント＆アドバイス
構成／桧貝卓哉 イラスト／横井智美 図版作成／永井俊彦