小１算数「10より大きい数」指導アイデア《数直線を用いて大小や順序について理解する》
執筆／埼玉県春⽇市⽴⼤⾕⼩学校教諭・渡邉駿嗣
監修／東京都国立教育政策研究所教育課程調査官・加固希支男、福岡県教育センター指導主事・西島大祐
目次
年間指導計画
・10までの数
・なんばんめ
・いくつといくつ
・いろいろな形
・あわせていくつ
・ふえるといくつ
・のこりはいくつ
・ちがいはいくつ
・長さくらべ・かさくらべ
・整理しよう
・10より大きい数
・何時 何時半
・３つの数の計算
・たし算
・ひき算
・形づくり
・たすのかな、ひくのかな
・20より大きい数
・どっちがひろい
・何時何分
単元の展開（各時の主な学習活動内容）
第１時 20までの数の数え方を知る。
第２時 20までの数の読み方、書き方を知る。
第３時 20までの数を「10といくつ」と数える。
第４時 20までの数の構成を知り、10といくつの和として捉える。
第５時 数直線を用いて、20 までの数についての大小を理解する。
第６時（本時）数直線を用いて、大小や順序について理解する。
第７時 10と１位数の加法と減法の計算の仕方を考える。
第８時 20までの数の構成を和や差で捉えて、計算する。（12＋３、15－３）
第９時 40までの数の数え方、読み方、書き方を知る。
本時のねらい
数は数直線上で、左から右に大きくなることに気付き、数と数の増え方から、数直線に入る数を選ぶことができるようにする。
評価規準
数の線に入る数を、両側の数の増え方・減り方から推測して入れることができる。
本時の教材のポイント
ここでは、10をこえる数は10といくつで表すとよいという前時までの学習内容を基に進めていきます。導入段階では、２つの数の大きさを比べる問題を複数提示します。それぞれの問題において、大小関係を確認した後、それら全ての数を小さい順に並べる活動を行います。すると、数が左から右に向けて大きくなっていくことに気付くことができます。しかし、数と数の間が空いていることから、「他にも数が入るのではないか」という焦点化した問題を子供が見いだすことができるようにします。
展開段階では、数を並べた間にどのような数が入るか確認をしていきます。そうすることで、数が左から１ずつ大きくなることを理解し、この図が「かずのせん」ということを教えます。そのあと、数の線を用いた空欄補充問題を複数提示します。その中に、２ずつ数が増える数の線を入れておくことで、数は１ずつ増えるものだと思っていた子供たちは、数の増え方が異なることに気付きます。「どうして２ずつ増えるのか？」ということを、前後の数を根拠に考える場を設定することで、数の見方を豊かにすることができます。
終末段階では、数の線を頼りに、指示された数がどこにあるか推測する問題を設定します。そうすることで、「基準となる数からいくつ増やしたらよいのか？」「いくつ減らしたらよいのか？」ということを適切に考えることができるようになり、加法・減法の考え方につなげることができます。
本時の展開
前の時間で、10より大きい数の表し方を学習しましたね。２つ数が出てきたら、どちらが大きいか決めることができますか。
できると思います。
どうやって比べるのですか。
10より大きい数同士なら、10といくつの「いくつ」で比べられます。
では、いくつか数の大きさを比べてみましょう。
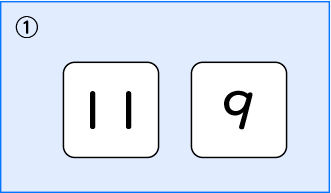
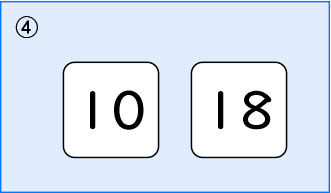
①は簡単だね。だって、11は10より大きいから、９よりも大きいはずだよ。
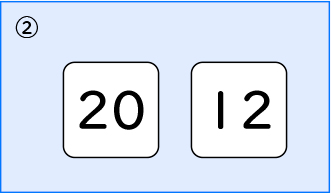
②は20だよ。だって、19の次が20だから、12より大きくなるはずだもの。
③は19のほうが大きいね。10といくつの「いくつ」で比べたら、９と７だから19だよ。
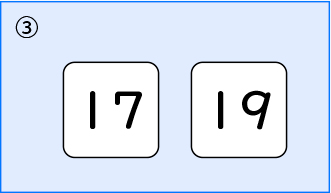
④は18だね。18は10よりも８も大きいからね。
みんな、２つの数を比べることができましたね。では、今まで出てきた数を全て使って、小さい順に並べることはできますか？
できます。小さい数から並べるから簡単だね。
でも、せっかく並べたのに、数が全部入っていませんね。他にどのような数が入るのでしょうね。
色々な数が入りそうだからやってみたいです。
並べた数の間に入る数を考えよう。
どのような数が入るでしょう。
９の前にはまだ数がありそう。０〜８が入りそうだよ。
９〜12はあるから、13から必要だね。
足りない数を考えて書き込んでみましょう。
見通し
並べたときに足りない数を付け足すとよいね。
０〜20までの数が全て入るとよいな。
自力解決の様子
Ａ つまずいている子
・適切な場所に正しい数を⼊れることができていない。全体での確認があった後も、適切な数の⼊れ⽅が分かっていない。
Ｂ 素朴に解いている子
・必要な数は理解できているが、数の線上に適切に表すことができていない。全体での確認があった後は、数を適切な位置へ⼊れることができる。
Ｃ ねらい通り解いている子
・適切な場所に正しい数を書き⼊れることができる。全体での確認のときに、どうしてその数が⼊るのか説明することができる。
全体発表とそれぞれの考えの関連付け
どこにどのような数が入りますか。
９が最初に来ているので、それより小さい数の０〜８を入れました。
なるほど。９よりも小さい数はたくさんありますからね。他にはどのような数が入りましたか。
12まではそろったので、13〜16が足りないです。
そうすれば、０〜20までの数がそろいましたね。
左から１ずつ数が大きくなっているから見やすいです。
そうですね。これを数の線と言います。では、この数の線を使った問題を解いてみましょう。
左右の数を見たら、すぐに14と16が入りそうだと分かります。
どうしてそのようにすぐ分かるのですか。
だって、13の次は14ですし、15の１つ前も14だからです。
同じように15の次は16ですし、17の１つ前は16だからです。
なるほど。前後の数から考えたのですね。では、これはどうですか。
あれ？おかしいな。12の次は13のはずだけれど、次の数が16になっているぞ。
大きいほうから見たら、16より１小さいから15だろうけれど、その下が12というのはおかしいね。
これは、２ずつ増えているのではないかな。
２ずつ増えるとはどういうことですか。
12より２つ大きい数は14です。14より２つ大きい数は16だから、12→14→16にすると数の並びとしてはおかしくないのではないかな。
確かに。そうしたら、□に入る数は14になるね。
そうだとすると、16の次は２増えて、18になりそうだね。
空いている□に14と18が入るから、12→14→16→18→20で２ずつ増える数の線ができあがるね。
数は１ずつ増えるのではなくて、２ずつ増えることもあるのですね。
まとめ
・数の線は、一番左が０で右に進むと数が大きくなる。
・数は１ずつだけでなく２ずつ増えることもある。
評価問題
①四かくに 入る かずを こたえましょう。
②14は どこに 入るでしょう。
ポイント＆アドバイス
構成／桧貝卓哉 図版／永井俊彦 イラスト／横井智美