小２算数「かけ算⑶」指導アイデア《｢倍」の意味に基づいて、１つ分の何倍かに当たる大きさの求め方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.04.08

単元の展開

第１時　九九表をつくり、九九表からさまざまなかけ算のきまりを見付ける。
▼
第２時　九九表から見付けたきまりを発表し合い、かけ算の掛ける数と積関係や交換法則、分配法則をまとめる。
▼
第３時　簡単な場合の被乗数が２位数のかけ算について、九九表を基に、学習してきたかけ算の性質やきまりを用いて答えの求め方を考える。
▼
第４時　九九を活用して、ものの数の求め方を、かけ算を用いて解決できるように工夫して考える。
▼
第５時（本時）「倍」の意味に基付いて、１つ分の何倍かに当たる大きさの求め方を考える。
▼
第６時　学習内容の定着を確認するとともに、数学的な見方・考え方をふり返る。

本時のねらい

｢倍」の意味を理解して図や式で表し、同じ倍の数であっても１つ分の大きさが違うと、１つ分の何倍かに当たる大きさも異なることに気付くことができる。

評価規準

・いくつ分を何倍と見ることを理解し、１つ分の何倍かに当たる大きさを求めたり、式に表したりしている。（知識・技能）
・同じ数だけ「倍」をした場合について、１つ分の大きさを基にして、１つ分の何倍かに当たる大きさの大小を判断することができる。（思考・判断・表現）

本時の展開

先生の育てたキュウリはどんどん大きくなり、最初の長さの３倍になりました。

３倍は聞いたことはあるけれど、どういうことかな。

キュウリの最初の長さと、最初の長さの３倍を図で表してみます。３倍とはどういうことかを、図を見て考えてみましょう。

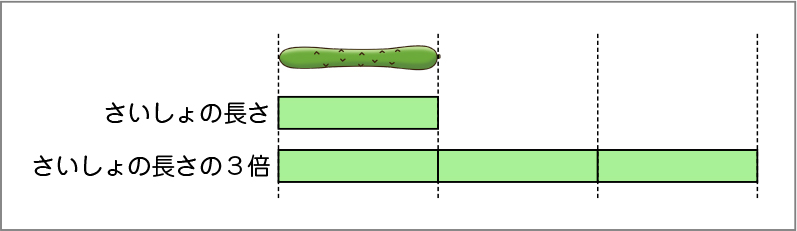
生活科で育てた野菜など、量が変化する様子について理解しやすい題材を、子供の身の回りの事象から選びましょう。｢最初の長さの３倍」の図を提示する際は、完成された図を見せるのではなく、｢最初の長さ」と同じ長さのテープを１本ずつ増やしていく様子を見せます。子供が「最初の長さ」を１つ分と見て、「３倍」が３つ分であることに気付きやすくなります。

最初の長さの「３倍」とは、どういうことでしょうか。

｢３倍」は、最初の長さの３つ分ということですね。

２つ分だったら「２倍」ですね。

２倍より３倍のほうが長くなるね。

何倍の数が大きいほど、長くなりそう。

え、本当にそうなのかな。

では、今日は、そのことを次の問題で考えてみましょう。

さいしょの長さとくらべて、今、ナスは２ばい、ピーマンは４ばい、オクラも４ばいの長さになりました。ナス、ピーマン、オクラのさいしょの長さは図の通りです。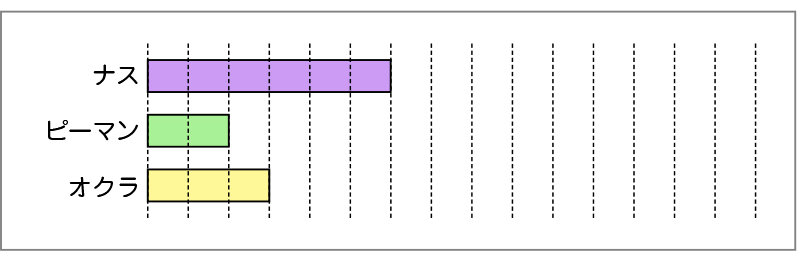

ナス、ピーマン、オクラの中で、今、一番長いのはどれでしょうか。

ナス、ピーマン、オクラの中で、今、一番長いのはどれだと思いますか。

ピーマンとオクラです。４倍で、倍の数が一番大きいからです。

ナスじゃないかと思います。最初の長さが一番長いからです。

ピーマンは、オクラより最初の長さが短いよ。４倍したら、どちらも一番長くなるのか分からない。

最初の長さが違っても、｢４倍」したら同じ長さになるのかな。　

見通し

何倍したときの長さは、どうすると分かりそうですか。

テープ図をかいてみます。

では、まず、ナスの長さを求めてみましょう。１めもりは１㎝として考えましょう。

Ａ　つまずいている子
｢最初の長さ」を１つ分と見ることができず、｢２倍なら２めもり伸ばす」などと誤って考え、｢ナスは６㎝＋２㎝＝８㎝」のように求めている。

Ｂ　素朴に解いている子
｢２倍は、最初の長さの２つ分」であることを理解し、テープ図を正しくかき、そのめもりを数え、｢ナスは12㎝」のように求めている。

Ｃ　ねらい通り解いている子
｢２倍は、最初の長さの２つ分」であることを理解し、テープ図を正しくかき、｢ナスは６㎝が２つ分だから、６×２＝12で12㎝」のように求めている。

学び合いの計画

乗法九九を構成する学習では、いつも同じ数を１つ分として扱ってきました。しかし、本時の学習では、異なる長さをそれぞれ１つ分と見る必要があるため、戸惑う子供がいることが予想されます。

｢何を１つ分と見るか」ということは、乗法の学習だけではなく、分数や除法、割合など多くの学習につながります。つまずいている子の考えを取り上げることで、｢何を１つ分と見るか」ということを全体で確認することが大切です。また、全体でテープ図をかきながら、｢何を１つ分と見て、いくつあるか」と考えたかについて、図に書き込んだり言葉で整理したりします。このような活動を通して、｢１つ分×いくつ分」という乗法の式の意味に基付いて、乗法の式に表すことができることに気付かせていきましょう。そして、乗法九九を用いれば、テープ図のめもりを数えなくても、計算で長さが求められることを実感させることが大切です。

また、初めに１つだけを指定して長さを求めるよう促し、その求め方を説明し合うことで「倍」の理解を確実にしたり、乗法九九で長さを求められることを共有したりします。その後で、残りの長さを求める活動を行います。このような流れにすることで、全員が「倍」を理解し、乗法を用いて式に表したり答えを求めたりできるかを評価することができます。