小２算数「かけ算⑵」指導アイデア《図や言葉、式を使って、加法や減法・乗法の演算決定を説明する》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.04.08

単元の展開

第１時　６の段の九九を構成する。乗数が１増えると、積は被乗数分だけ増えることを理解する。
▼
第２時　６の段の九九の呼称を知り、唱える。６の段の九九を用いて、問題を解決する。
▼
第３時　７の段の九九を構成する。乗数が１増えると、積は被乗数分だけ増えることを理解する。
▼
第４時　７の段の九九の呼称を知り、唱える。７の段の九九を用いて、問題を解決する。乗数の交換法則が成り立つことに気付く。
▼
第５時　８の段の九九を構成する。８の段の九九の構成を通して、答えの増え方や交換法則に気付く。
▼
第６時　８の段の九九の呼称を知り、唱える。８の段の九九を用いて、問題を解決する。
▼
第７時　９の段の九九を構成する。９の段の九九の構成を通して、答えの増え方や交換法則に気付く。
▼
第８時　９の段の九九の呼称を知り、唱える。９の段の九九を用いて、問題を解決する。
▼
第９時　１の段の九九を構成する。１の段の九九の呼称を知り、唱える。１の段の九九を用いて、問題を解決する。
▼
第10時（本時）問題文の仕組みを読み取って加法や減法・乗法の演算決定をし、乗法の理解を深める。具体物の操作を基に、解き方や絵や図、式や数字、言葉を使って分かりやすく説明する。
▼
第11時　学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。

本時のねらい

加法や減法・乗法の演算決定について、問題文の仕組みを読み取り、具体物を操作する活動を通して、図や式、言葉を使って説明することができる。

評価規準

図や言葉、式を使って、加法や減法・乗法の演算決定を説明することができる。

本時の展開

少しずつ問題を見せます。どんな計算になるでしょうか。

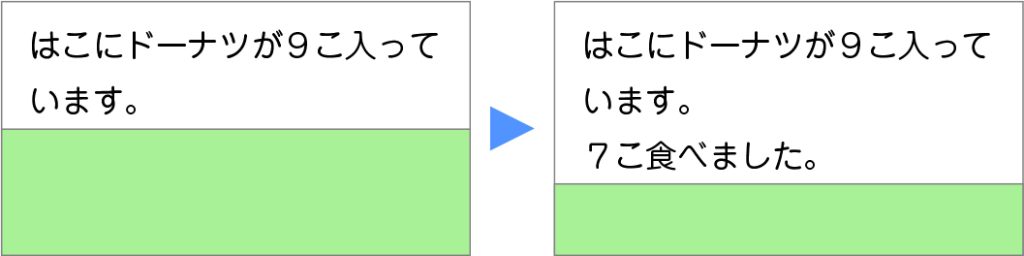
ひき算だと思います。

式は９－７です。

続きは「残りは何個でしょう」だと思います。

続きを見ていきましょう。

やっぱりそうだ。

図を使って表すことができますか。

まず、〇を９個かきます。７個食べたので、７個×をつけます。残りが２個だから、答えは２個です。

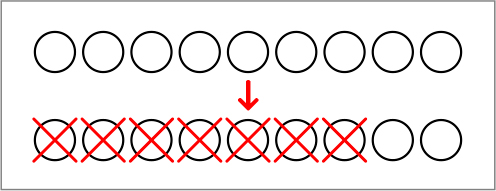
９－７＝２の計算になります。

次はどんな計算になるでしょうか。

これはたし算だ。

｢全部で」があるから

続きを見てみましょう。

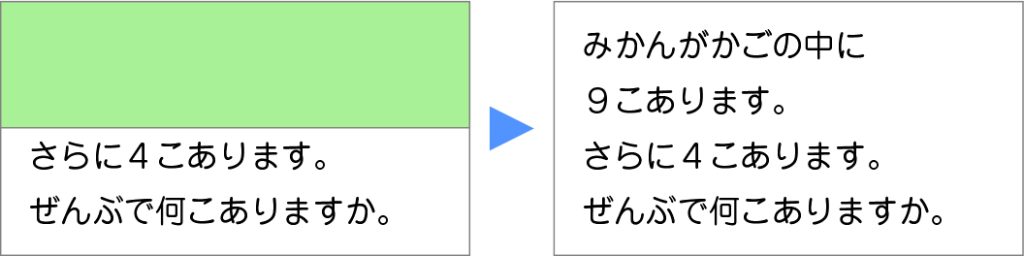
やっぱりたし算だ

９＋４だね。

では、これも図を使って表すことができますか。

まず、〇を９個かきます。次に〇を４個かきます。合わせると13個になります。

９＋４＝13です。

次はどんな計算になるでしょうか。

｢全部で」があるから、またたし算だ。

続きを見てみましょう。

あれ？　これはたし算じゃないと思う。

これはかけ算じゃないかな。

７×３だね。

え？　３×７じゃないの。

１人１台端末活用アイデア①
問題文を提示する際にタブレットを活用しましょう。一文ずつ見せることで、視点が焦点化され、子供に気付いてもらいたいところが見やすくなります。減法の問題文では、上から問題文を見せることで「食べました」という言葉からひき算と気付かせます。また、加法の問題文では、下から見せることで「ぜんぶで」という言葉からたし算と気付かせます。ただし、乗法の問題文も下から見せることで「ぜんぶで」という言葉に意図的に着目させます。続きの問題文を見せることで、乗法の問題文だと気付かせ、｢ぜんぶで」という言葉があるからといってすべてがたし算になるのではないことを押さえましょう。

正しい式は、どうすれば分かるかな。

見通し

どうしたら正しい式が分かるでしょうか。

たし算とひき算のときと同じように図に表せば分かると思います。

鉛筆を使って数えたいです。

ブロックを使えば分かると思います。

自力解決の様子

Ａ　つまずいている子
７つの〇を１まとまりにして、そのまとまりを３つかいている。（７×３＝21）

Ｂ　素朴に解いている子
３つの〇を１まとまりにして、そのまとまりを７つかいている。（３×７＝21）

Ｃ　ねらい通り解いている子
３つの〇を１まとまりにして、そのまとまりを７つかき、３が１つ分で７がいくつ分になることを図や言葉を使って説明している。

学び合いの計画

問題文に書かれている数字の順番で計算をしている子供は少なくないと考えられます。とくに乗法の問題では、乗数と被乗数を入れ替えて計算してしまう子供がよく見られます。これらの子供は１つ分といくつ分についての理解が不十分である可能性があります。そのため、乗法の場合は問題文に書かれている順番ではなく、１つ分といくつ分がどこに書かれているのかを読み取る活動が大切になってきます。

自力解決後、４人グループで自分の考えた図やブロックを示しながら１つ分といくつ分について説明させる活動を行います。この学び合いを通してＡ段階の子供は、１つ分が７ではなく３であることに気付くことが期待されます。

全体発表の際には、１つ分といくつ分を判断した根拠を問い、問題文の「１人に～」や「～ずつ」という記述に着目させます。また、｢７×３にした人の気持ちは分かりますか」と問い、間違えた子供の気持ちに寄り添い、これまでの経験から問題文の順番通りにしたほうがよいと思ったのではないかという論理に気付かせたいものです。そして、「答えが同じならば、７×３でもよいのではないか」と問います。子供からは７×３では、１人に７本ずつあげることになることを言葉にさせ、答えが同じになるからといって１つ分といくつ分を入れ替えてはいけないことを確認しましょう。