小４算数「角とその大きさ」指導アイデア《180°より大きい角度の測定の仕方を説明する》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.07.03

単元の展開

第１時　半直線を回転させると、いろいろな大きさの角ができることを理解する。
▼
第２時　分度器の観察を通して、角の大きさの単位「度（°）」を知り、角の大きさの表し方を理解する。
▼
第３・４時　分度器を用いて角の大きさを測定することができる。
▼
第５時（本時）180°より大きい角度の測定の仕方を、既習の分度器を用いた角度の測定の仕方を基に考え、説明することができる。
▼
第６・７時　分度器を使って角をかいたり、三角形をかいたりすることができる。
▼
第８時　単元の学習の活用を通して事象を数理的に捉え、論理的に考察し、問題を解決する。
▼
第９時　学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り価値付ける。

本時のねらい

180°より大きい角度の測定の仕方を、既習の分度器を用いた角度の測定の仕方を基に考え、説明することができる。

評価規準

・180°や360°の角に着目して、図や式から他者が考えた過程を読み取り、式にしたり説明したりしている。（思考・判断・表現）
・対話的に粘り強く問題解決に取り組むとともに、180°より大きい角度の測定の仕方を考えた過程をふり返り、学習に生かそうとしている。（主体的に学習に取り組む態度）

本時の展開

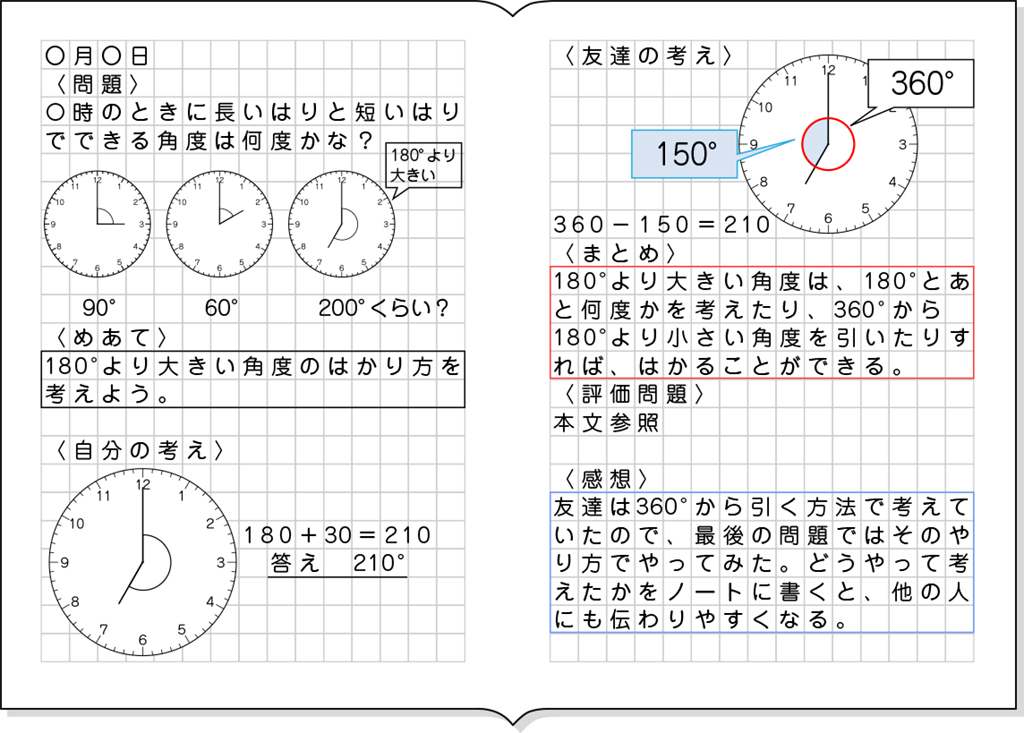
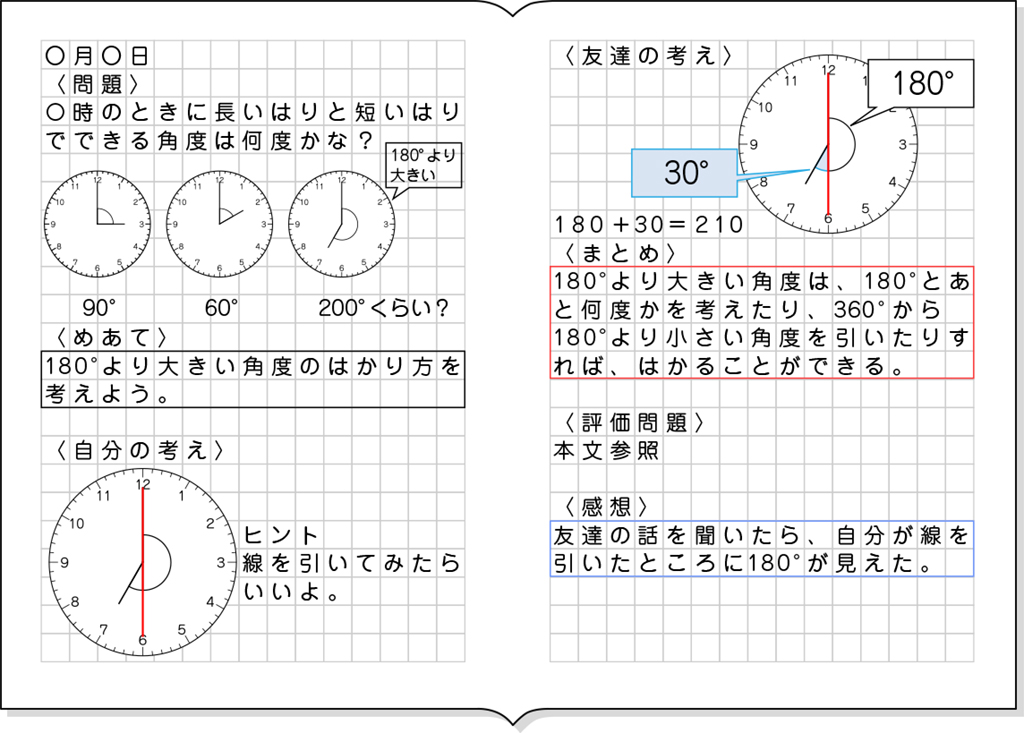
本実践は時計の短針と長針がつくる角度について考える展開とします。例えば６時であれば、長針と短針が一直線になるので、角度は180°になります。１つの時計から、短針と長針を動かすことで、さまざまな角度をつくることができます。時計の形が円であることや、時計の針が回転して進むことから１周で360°という回転の角度もイメージしやすいです。

まずは、直角がすぐに見える３時を提示します。そこから２時を提示し、分度器の使い方や分度器を使わずとも分かる角度について、既習をふり返っていきます。そして、本時の課題である７時を提示します。既習の角度から順に提示することで、180°を越えた角度について、｢どのように求めることができるのだろう？」という問いを生み出すことができるとともに、180°を越えた場合について、解決の見通しをもつことができます。

今日は時計の長針と短針でできる角度を考えてもらいます。まずは３時です。

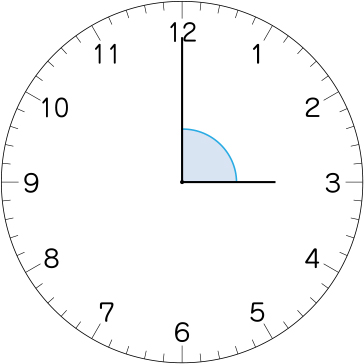
90°です。

どうして90°だと分かるのですか。

直角になっているからです。

本当に直角になっていますか。

三角定規を使えば確かめることができます。

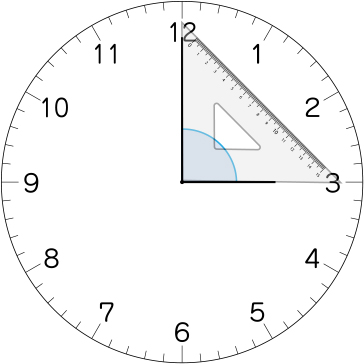
確かに90°ですね。３時は90°になるんですね。では、次は……。

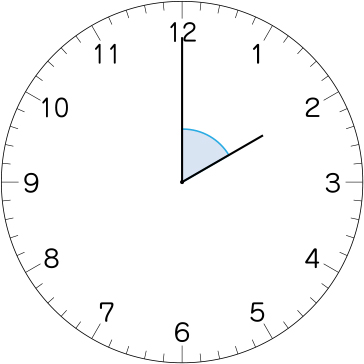
今度は２時だ。分度器を使えば測ることができます。

では、測ってみてください。

測ったら60°になりました。

分度器を使えば、角度を測ることができますね。

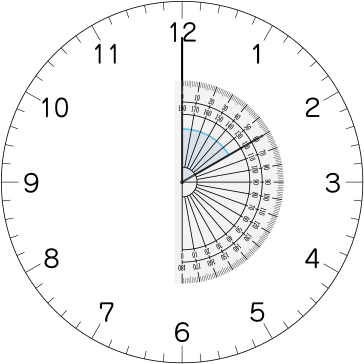
では、次は……。

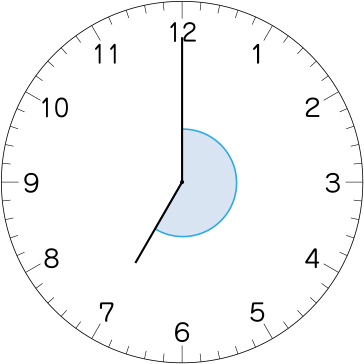
あれ？　ちょっと大きい。

分度器で測ることができないんじゃないかな。

分度器は180°までしか測ることができないのに、これはそれよりも大きい。

そうですか。180°を越えている角度だから難しいんですね。どうすれば、こうして180度より大きい角度も測ることができるでしょうか。

180°より大きい角度の測り方を考えよう。

見通し

分度器では測れませんか。だいたい何度くらいになりそうですか。

200°くらいなんじゃないかな。

どうして200°くらいと思ったのですか。

180°よりも大きいからです。

だったら、工夫すれば測ることができるんじゃないかな。

線を引けばいいんじゃないかな。

自力解決の様子

Ａ　つまずいている子
どう測ったらよいかが分からない。

Ｂ　素朴に解いている子
240°という角度を求めることはできているが、どのように求めたかの説明を表現することができない。

Ｃ　ねらい通り解いている子
180°や360°を基にして角度を求めることができ、その求め方の説明を表現することができている。

自力解決の様相から、子供たちの状況を評価します。このときの評価は、｢記録に残す評価」というよりは、｢指導と評価の一体化」を意識することが大切です。子供の状態が、上記のＡ・Ｂ・Ｃのどれにあたるのかを把握します。そして、どのような指導をするのかを考えていきます。特にＡの子供に対してどのような指導をするか考えます。ICTを活用しながら、｢線を１本引いてみたらどうかな？」と、補助線を引くように促したり、角度のなかに既習の角度が見えないかを問うたりすることで、解決の糸口を見付けることができるようにします。

また、解決が難しいと感じている子が多いと判断したときには、自力解決の手を一度止め、｢困っている人がいるけど、この人たちが『あっ！』と思うようないいヒントはないかな？」と解決が進んでいる子に投げかけるのも一つの方法です。そうすることで、困っている子は解決の糸口を見付けることができます。また、解決が進んでいる子は、自分がどうして解決に向かうことができたのかをふり返る時間となります。｢180°を考えるといいよ」｢線を引くと見えてくるよ」｢どんな角度だったら分かりそうかな？」というようなヒントが期待できます。

学び合いの計画

学び合いのねらいは、180°や360°を基にして、180°＋□°や360°－□°として求めることを、図と式と分度器の操作とを関連付けていくことです。解決した方法を黒板の前でただ発表していくのもよいですが、ICTを活用し、一人一人の考えを実際に操作する時間をもつことも効果的です。その際、考えをそのまま伝えるのではなく、式のみを提示し、その式から、どのような補助線を引き、どのように分度器を操作して考えたかをタブレット上で操作するような活動を取り入れるのもよいでしょう。

ノート例

Ｂ　素朴に解いている子

Ａ　つまずいている子

全体発表とそれぞれの考えの関連付け

どのように測ったのか、みんなで考えていきたいと思います。最初に○○さんですが180°＋30°という式で考えたようです。

分かった。180°のところで線を引いたんだと思います。

どういうことですか。みなさん、○○さんがどうやって考えたのかをタブレット上で操作してみてください。

このように、まず、180°のところで線を引いて、そこからはみ出している部分を分度器で測ると30°だから、180＋30＝210になって、この７時のときの角度は210°になります。180°は測らなくでも角度が分かるから、線を引くと、180°とあとどれくらいと考えることができます。

〈□□さん〉私は違う式になる考え方です。

どんな式になったのか、教えてください。

360－150＝210です。

確かにこれも210°になるということは、答えは合っていますね。どのように考えたのか分かりますか。

この１周回った角度は360°になります。そして、この色を付けた部分の角度を測ると、ここが150°になります。全体の360°からこの150°を引くと、７時の角度を求めることができます。

さっきはたし算だったのに、今度はひき算なんですね。考え方が違うんですね。

でも、同じところもあります。

どんなところが同じなのですか。

○○さんは、180°、□□さんは360°だけど、測らなくても分かる角度を使って、その残りの部分を分度器で測って角度を求めています。

なるほど。違う考え方のようで、同じところを見付けることができたんですね。すばらしいです。

※１人の子の式表現を実際に操作するなかで、Ａの子のような解決に向かうことが難しかった子供に対しては、どのように補助線を引いているのか、どのように既習の角度を見いだそうとしているのかをよく観察し、｢よく線を引くことができたね」｢△△さんも、測らなくても分かる180°が見えたんですね」とほめ、価値付けることが大切です。また、最後には、２つの方法に共通することを問い、｢測らなくても分かる角の大きさがポイント」だと言語化させましょう。

180°より大きな角度は、どのようにして測ることができましたか。

測らなくても分かる角度を考えて、線を引いて180°＋□°と考えたり、360°－□°と考えたりして求めることができました。

180°より大きい角度は、180°とあと何度かを考えたり、360°から180°より小さい角度を引いたりすれば測ることができる。

評価問題

11時のときの角度は何度かな？

子供に期待する解答の具体例

180°＋150°

360°－30°

※評価する視点としては、｢測らなくても分かる角度を基にして角度を求めている」ということですが、今回のような360°に近いときには、360°－30°のような求め方のほうがより求めやすいことなどを話し合うことも子供たちの思考力・判断力・表現力を育成するためには大切なことです。

感想例

今日は180°より大きな角度の測り方を考えました。最初はどうやって考えたらよいか分からなかったけど、Ａさんが話していた「線を引いたらいいよ」というヒントで、180°が見えました。次の問題でも、線を引いてみたら、今まで勉強した角度が出てくるのかなと思いました。
今日は180°＋□°という考え方と、360°－□°という２つの考え方が出ました。求める角度の大きさが360°に近いときには360°－□°の求め方のほうが簡単だと思いました。求める角度によって、やり方を変えてみたいなと思いました。

イラスト／横井智美

【関連記事】

1人1台端末時代の｢教科指導のヒントとアイデア｣シリーズはこちら！