小２算数「かけ算⑶」指導アイデア《９の段の九九の構成を通して、答えの増え方や交換法則に気付く》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.04.24

単元の展開

第１時　６の段の九九を構成する。乗数が１増えると、積は被乗数分だけ増えることを理解する。
▼
第２時　６の段の九九の呼称を知り、唱える。６の段の九九を用いて、問題を解決する。
▼
第３時　７の段の九九を構成する。７の段の九九でも、乗数が１増えると、積は被乗数分だけ増えることを理解する。
▼
第４時　７の段の九九の呼称を知り、唱える。７の段の九九を用いて、問題を解決する。乗数の交換法則が成り立つことに気付く。
▼
第５時　８の段の九九を構成する。８の段の九九の構成を通して、答えの増え方や交換法則に気付く。
▼
第６時　８の段の九九の呼称を知り、唱える。８の段の九九を用いて、問題を解決する。
▼
第７時（本時）９の段の九九を構成する。９の段の九九の構成を通して、答えの増え方や交換法則に気付く。
▼
第８時　９の段の九九の呼称を知り、唱える。９の段の九九を用いて、問題を解決する。
▼
第９時　１の段の九九を構成する。１の段の九九の呼称を知り、唱える。１の段の九九を用いて、問題を解決する。
▼
第10時　問題文の仕組みを読み取って加法や減法・乗法の演算決定をし、乗法の理解を深める。具体物の操作を基に、解き方や絵や図、式や数字、言葉を使って分かりやすく説明する。
▼
第11時　学習内容の定着を確認するとともに、数学的な見方・考え方についてふり返る。

本時のねらい

９の段の九九の構成の仕方を考え、説明することができる。

評価規準

乗法の意味や性質を用いて、９の段の九九の構成の仕方を考え、説明している。

本時の展開

みなさん、今までの学習で何の段をつくってきましたか。

２～８の段です。

そうですね。２～８の段を一緒につくってきました。どのようなきまりを使ってつくりましたか。

例えば、６×３は６＋６＋６=18というように、たし算を使ってつくりました。

６の段では６×１＝６、６×２=12と、答えが６ずつ増えるきまりを使ってつくりました。

８の段の答えは、５の段の答えと３の段の答えを足した数になっているというきまりも使えました。

掛けられる数と掛ける数を入れ替えても、答えが同じというきまりも使えました。

かけ算のきまりを使って、いろいろな段の九九をつくることができましたね。それでは、まだ一緒につくっていない段は何の段でしょうか。

１の段です。

９の段です。

そうですね。あと２つの段をつくることができれば、九九表が完成しそうですね。今日は、今まで学習したきまりを使って９の段をつくっていきましょう。

９のだんの九九をくふうしてつくりましょう。

では、９の段を「くふうしてつくる」とはどういうことでしょうか。

今まで学習したことを使って考えるということだと思います。

今まで使った作戦やきまりを使って考えることだと思います。

そうですね。では、今までの学習を生かして、９の段を一緒につくっていきましょう。

９の段の九九のつくり方を考えよう。

見通し

掛ける数が１増えると、かけ算の答えが掛ける数分増える、「ふえふえさくせん（累加）」が使えそう。

９×２と２×９は答えが同じという「はんたいさくせん（交換法則）」が使えそう。

表を見て、９の段を分けて考える「わけわけさくせん（分配法則）」を使えば分かりそう。

自力解決の様子

Ａ　つまずいている子
・９の段の九九の答えは求められたが、説明することができないでいる。
９×１＝９　９×２＝18　９×３＝27　……

Ｂ　素朴に解いている子
・９の段の九九の構成を、累加を使って考えている。
９×１＝９　
９×２＝18　９＋９
９×３＝27　９＋９＋９　……

Ｃ　ねらい通り解いている子
・交換法則
９×２の答えは、２×９＝18と同じになるので18です。
９×３の答えは、３×９＝27と同じになるので27です。……

・かけ算のきまり
掛ける数が１増えると、答えは９ずつ増えることを使いました。
９×１＝９
９×２＝18　９＋９
９×３＝27　18＋９　……

・分配法則
９×９の答えは、５×９の答えと４×９の答えを足せば求めることができます。

学び合いの計画

９の段では、今まで学習したかけ算の意味や性質を用いてつくり上げることが大切です。

自力解決の場面では、子供は今までの学習を基に、自分なりのやり方で９の段を構成していきますが、手が止まり、自分で考えをまとめることが難しい子供には、９の段のアレイ図をヒントカードとして渡したり今までのきまりが使えないか助言したりするなど、ていねいに支援することが大切です。

また、アレイ図を端末上に表示してきまり（交換法則・分配法則）を確認させたり、今までの学習をふり返ることができるページを配信したりすることで、自分で考えをまとめられるように促すことも有効です。

また、乗法の性質を使って式のみで考えている子供には、九九表やアレイ図を用いるように声をかけ、式と図の関連性に気付かせるようにすると九九への理解が深まるでしょう。

比較・検討の場面では、累加の考えに固執しないようにすることが大切です。８の段までに学習した乗法の性質や交換法則・分配法則の有用性が分かるように話合いを展開し、今まで習ってきた九九と同じように、かけ算の意味や性質を使えば９の段をつくることができるというまとめにつなげていくことが大切です。

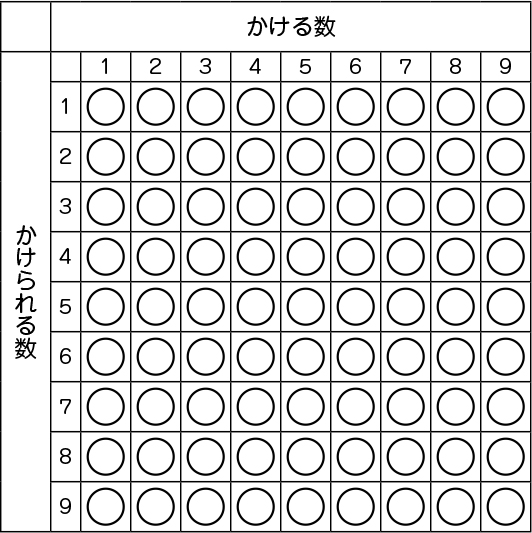
ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

どのように９の段の九九をつくりましたか。

８の段の九九をつくるときまで考えたように、「ふえふえ作戦」を使い、９を足して考えました。９を順に足していけば、９の段をつくることができます。

なるほど。「ふえふえ作戦」を使って、９が何個分あるかをたし算で考えたのですね。９が何個分あるかは、どのように考えたらよいでしょうか。

掛ける数と同じ数にします。９×３なら、×３なので９が３個分で９＋９＋９です。

でも、掛ける数が大きくなると、たし算が大変だね。

確かに９×９で９を９個足すのは大変だね。

私は、９＋９＋９……と９を足していくのは大変なので、今まで学習した「掛ける数が１増えると、答えが掛けられる数分増える」というきまりを使って考えました。

２つ目の考え方のよさは何でしょう。

答えを求めるときに、たし算が１回で済むので、計算が早く正確にできます。

掛ける数が大きくなったときにも、１つ前の答えが分かればすぐに答えを求めることができます。

では、ほかのきまりを使って考えた人はいませんか。

私は「はんたい作戦」で、逆にして考えました。９×１＝９。９×２＝18は、２×９＝18と同じです。同じように考えて、９×３＝27は、３×９＝27です。９×４＝36は、４×９＝36です。反対にして考えると、９の段の九九をつくることができました。

掛けられる数と掛ける数を反対にして考えるよさは何ですか。

たし算を使わずに、今まで習ったかけ算だけで考えることができます。

今まで学習した計算で９の段の九九をつくることができます。

９×８までは答えを求めることができますね。では、９×９はどのように考えますか。

「ふえふえ作戦」のきまりを使えば、９×８＝72に９を足して、72＋９＝81と答えを求めることができます。

図（アレイ図）を使って考えた人もいました。

９×９を「わけわけ作戦（分配法則）」を使って考えました。掛けられる数の９を５と４に分け、５の段と４の段の答えを求めて後から足しました。９×９は５×９と４×９の答えを足せば求めることができます。

「わけわけ作戦」で掛けられる数の９を分けて計算するよさは何でしょうか。

９×１～９×９まで、今までに学習したことですべてを求めることができます。

掛ける数が大きくなっても計算しやすいことです。

今日は、今までの学習を生かして９の段をつくりました。どのようにして９の段の九九をつくったか、ふり返りましょう。

８の段まで九九をつくってきた方法と同じように、９を足していくたし算でつくることができます。

掛ける数が１増えると９ずつ増えることを使うと、簡単に９の段をつくることができます。

図を使って、９を分けて考えると９の段をつくることができます。

今まで学習したかけ算のきまりを使って、９の段がつくれましたね。どんなきまりを使ったか、まとめましょう。

今まで習ってきた九九と同じように、かけ算のきまりを使えば９の段をつくることができる。
・掛ける数だけ９を足して求める。
・掛ける数が１増えると答えは９増えるきまりを使う。
・９のかけ算の逆のかけ算を使う。
・９を５と４に分けて考える。

評価問題

かけ算のきまりをつかって、12×３の答えをもとめましょう。また、そのわけを書きましょう。

子供に期待する解答の具体例

12×３は12＋12＋12だから、12×３＝36です。
掛ける数が１増えると答えが12増えるので、12×１＝12、12×２＝12＋12＝24、12×３＝24＋12＝36、12×３＝36です。
12×３は３×12と同じ答えになるので、３×10＝30。あと６を足して12×３=36です。
12を９と３に分けて、９×３=27、３×３＝９。27＋９＝36。12×３＝36です。

感想例

掛ける数が１増えると、答えは９ずつ増えるきまりを使えば、９の段も簡単につくることができる。
図と式を合わせて考えると分かりやすかった。次から、式の計算のきまりだけではなく、図も書いて考えるようにしていきたい。
これまで９＋９＋９……、という計算をして答えを出していたけれど、答えは９ずつ増えるから、前の答えに９を足せばよいことが分かった。９＋９＋９……の計算をするよりも、早く、簡単に、正確に答えを出すことができる。
これまでに見付けたきまりを使って、９の段の九九をつくることができた。九九表にはないけれど、10の段やそれ以上の段も、今までと同じきまりを使ってつくってみたい。

１人１台端末活用アイデア

自力解決で考え方がまとまった子供は、タブレットで写真を撮り、共有アプリ（Teamsやスクールタクトなど）に投稿させる。共同閲覧ができる設定にしておき、考えがまとまらない場合には、各自閲覧することで考えるヒントにさせる（紙で配っていたヒントカードの代わりにする）。
発表場面では、子供の考え方が書いてあるノートを大型テレビや電子黒板に映し出すようにする。また、可能な限り、全員の端末に画面を共有することで、座席の位置に関わらず、適切な大きさで見せたい資料を提示することができる。
アレイ図は端末上で操作できるようにし、鉛筆などで○をかく作業や消す作業をなくすことで、効率的に自力解決を進めることができるようにする。

ワークシート（ダウンロード可）

ダウンロードはこちら＞＞