小6算数「6年のまとめ②(考える方法と表現)」指導アイデア
執筆/埼玉県公立小学校教諭・白田飛鳥
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
考える方法を1時間、考えるときの表現を1時間で扱う。本時は2/2時
ねらい
物事を数理的に考える際の数学的表現の機能やそのよさについて再確認し、意義付ける。
評価規準
石を正三角形状に並べ、大きくしていく際の正三角形の1辺に使われる石の個数と総数の関係についての問題について、考えるときの表現(表、式、図)を用いて解決することができる。
問題場面
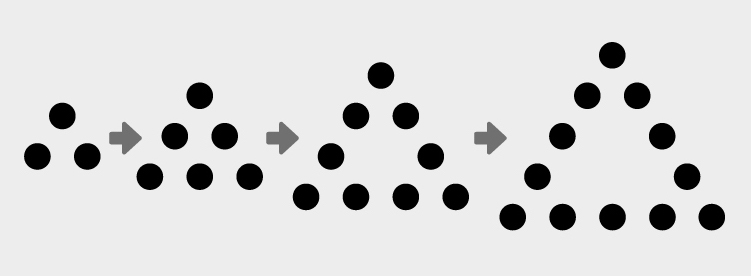
下の図のように1辺の石を1つずつ増やしながら並べて正三角形を作っていきます。
1辺に使う石の数が50個のとき、正三角形を作っている石は全部で何個ありますか。
図のように1辺の石を1つずつ増やしながら並べて正三角形を作っていきます。1辺に使われる石の個数が50個のとき、石の個数が全部で何個になるか考えていきます。
50個も並べると、すごく大きな正三角形ができるね。石もすごく多いんじゃないかな。
図をかいて数えればいいんじゃないかな。
1辺が50個の場合は石の数が多すぎて、図にかくのが大変です。
表を書いて、増え方にきまりがあるか調べてみるといいと思います。
うまく言葉の式で表せるといいんだけれど……。
きまりを見付け、1辺に使う石の数が50個のとき、正三角形を作っている石は全部で何個になるか個数を求めましょう。
本時の学習のねらい
使われる石の数のきまりを見付け、どのように考えたか説明しよう。
見通し
きまりを見付けるにはどんな方法があるかな。
図をもう少し増やしてみて、いつでも同じ数え方ができないか調べてみたい。
1辺に使われている石の個数と全部の個数の関係を表にしてみると、見付けやすそう。
少ない個数の場合で考えて、いつも同じ式の形で全部の個数を表せないかな。
自力解決の様子
A つまずいている子
図をかくことはできるが、きまりを見付けることができない。
B 素朴に考えている子
表に整理することができ、1辺の石が1つ増えると、全体で3個ずつ増えるきまりがあることに気付いている。
C ねらい通り解決する子
図や表からきまりを見付け、式に表している。式に表すことでどんな正三角形でも合計の個数が求められることを理解している。
学び合いの計画
自力解決では、きまりを見付け、どのように考えたか説明できるようにします。1つの方法でできたら、他の表現方法を考えさせます。
イラスト/横井智美
『教育技術 小五小六』2022年2/3月号より