小5算数「割合」指導アイデア《割合を用いた二つの数量の比べ方》
執筆/福岡県福岡市立席田小学校教諭・馬場祐樹
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 シュートの入った回数とシュートした回数の関係に着目し、一番よく成功した人の比べ方を考える。
▼
第2時(本時)シュートの入った回数とシュートした回数の関係に着目し、倍の意味を基にして、割合を用いた二つの数量の関係の比べ方について考える。
▼
第3時 二つの数量の関係に着目し、百分率や歩合での表し方を考える。
▼
第4時 基準量、比較量、割合の関係に着目し、基準量と割合から比較量を求める方法を考える。
▼
第5時 基準量、比較量、割合の関係に着目し、比較量と割合から基準量を求める方法を考える。
▼
第6時 割合の適用問題に取り組む。
▼
第7時 和や差を含んだ割合の表現に着目し、基準量と割合から比較量を求める方法を考える。
▼
第8時 学習内容の生活への活用
▼
第9時 学習内容の習熟・定着
本時のねらい
シュートの入った回数とシュートした回数という二つの数量の関係に着目し、どのチームが一番シュートが成功したかを考える活動を通して、基準量を1と見たときに、比較量がどれだけに当たるかで比べる方法について考える。
評価規準
二つの数量の関係を比べるときに、全体を1と見て、部分の大きさを表して比べることができる。(知識・技能)
本時の展開
※本時の前の時間では、プロローグとして、次のような学習を位置付けておきます。ここでは、概略だけ記します。
下の表で、だれが、シュートが一番よく成功したと言えるかについて考えていきます。
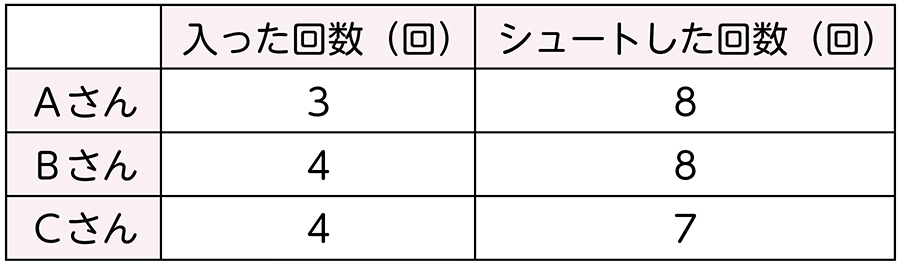
授業の導入では、これらの表をすべて提示するのではなく、まず入った回数だけを提示します。そして、どのチームが一番よく成功したかを決めるためには、入った回数だけではなく、「入った回数」と「シュートした回数」という二つの数量に着目して、それらの量の関係を考える必要があることに気付かせます。
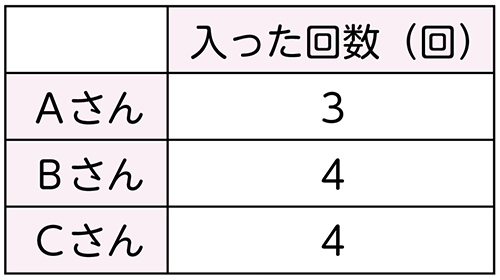
BさんとCさんは、Aさんより成功しています。
入った数が多くても、投げた数が多いと、よく成功したとは言えないと思います。
そして、次のようなことを理解させ、プロローグとします。
- シュートのうまさを調べるためには、「入った数」と「シュートした回数」の二つの数量から判断しないといけない。
- AさんとBさんを比較すると、シュートした回数が同じなので、入った回数の多いBさんのほうが成功している。
- BさんとCさんを比較すると、入った回数が同じなので、シュートした回数が少ないCさんのほうが成功している。
- Bさんはちょうど半分入っている。Cさんの入った回数は半分より多いので、BさんとCさんでは、Cさんのほうが成功している。また、Aさんの入った回数は半分より少ないので、AさんとBさんだとBさんのほうが成功している。
※本時では、次の場面を考えます。

㋐・㋑・㋒・㋓の四つのチームでバスケットボールの試合をしました。シュートが一番よく成功したと言えるのは、どのチームになりますか。試合でのシュートの記録は、以下の表のとおりです。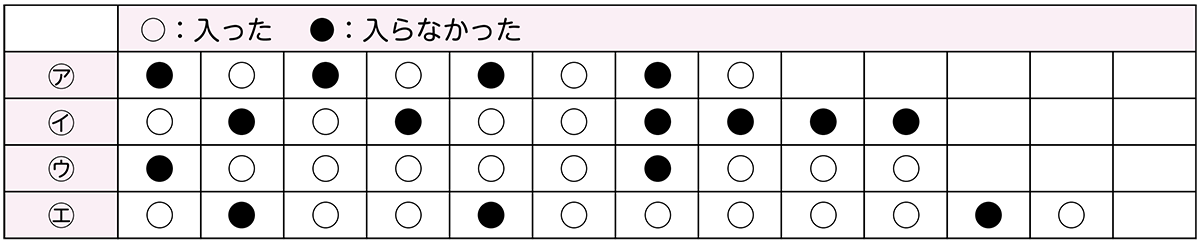
導入ではまず、前時のプロローグで、「だれが、シュートが一番よく成功したと言えるか」を考えたことを想起させながら、本時の問題を提示し、「どのチームが、シュートが一番よく成功したと言えるか」を本時も考えていくことを全体で確認します。
チーム名をクラスの班に変えたりすることで、より問題場面に興味をもたせることもできます。
表を提示する際には、はじめから結果をすべて提示せず、各チームの結果をプレゼンテーションで少しずつ提示することで、結果に興味をもたせながら、それぞれの数値に着目させていきます。
前回、バスケットボールの練習で、「だれが、シュートが一番よく成功したと言えるか」について考えましたね。今日は、その後の試合のシュート結果になります。
※プレゼンテーションを使って、場面を段階的に提示する。
どのチームが、シュートが一番よく成功したと言えますか。
○が一番多そうな㋓チームかな。
この表だと分かりにくいから、もっと見やすく整理したいな。
それでは、それぞれのチームのシュート記録を見て、前時のように「入った数」「シュートした数」を表に整理してみましょう。
※下記の表に整理させる。
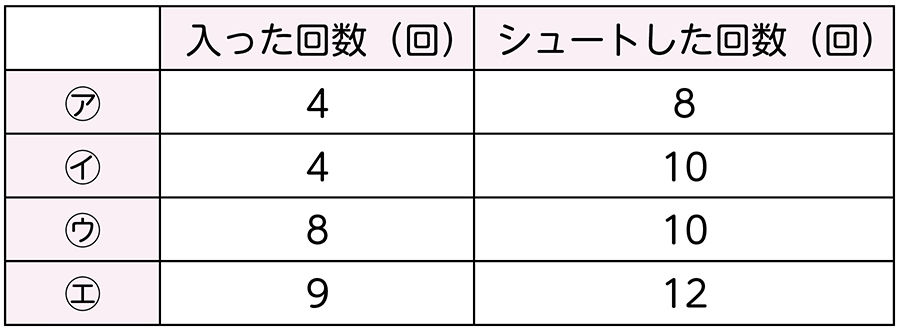
このなかで、すぐに比べられるチームはありますか。
㋑チームと㋒チームです。
なぜ、㋑チームと㋒チームはすぐに比べられるのですか。
㋑チームと㋒チームでは、シュートした回数が同じなので、入った数で比べると、㋒チームが多いからです。
同じような考え方で、ほかにもすぐに比べられるチームはありますか。
㋐チームと㋑チームです。㋐チームと㋑チームでは、入った数が同じなので、シュートした数が少ない㋐チームのほうが、よく成功したと言えます。
では、㋐チームと㋒チームと㋓チームでは、どのチームが一番よく成功したと言えますか。
入った数もシュートした数も違うので、すぐには比べられません。どうすればいいかな。
では、今日はそれをみんなで考えましょう。

入った数もシュートした数も違うときの比べ方を考えよう。
見通し
前時で学習した、「半分より多い・少ない」という考えを想起させます。
㋐チームに着目し、半分入っていることを倍で表現していくことを通して、「入った数はシュートした数の何倍」という見方で、半分より多く入っている㋒チームと㋓チームの比べ方に絞って考えるように方向付けます。
前の時間でちょうど半分入っているチームがありました。㋐チームと㋒チームと㋓チームの三つのなかで、ちょうど半分入っているチームはありますか。
㋐チームです。

「半分入っている」ということを8回や4回という数を使って言えますか。
8回の半分の4回入っています。
今度は倍という言葉を使って言えますか。
8回は4回の2倍になっています。
その通りです。4回を基にすると8回は2倍に当たりますね。それでは8回を基にするとどのように言えますか。
4回は8回の0.5倍になっています。
4回や8回を入った数やシュートした数という言葉で置き換えて言えますか。
入った回数はシュートした回数の0.5倍です。
0.5倍ということを数直線で確認してみましょう。シュートした回数8回と、入った回数4回をまず書きます。
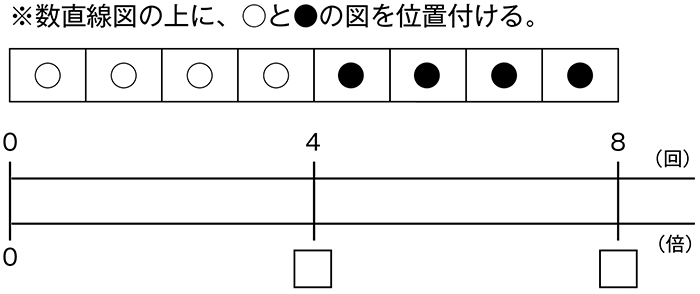
0.5は、どちらの□に入れたらよいでしょうか。(子供とやりとりしながら、進める)
4回が0.5倍に当たるから、4の下の□が0.5だと思います。
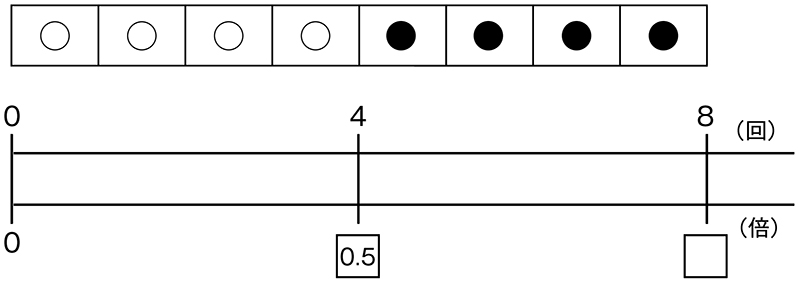
8の下の□には何が入りますか。
1だと思います。
どうして1が入るか説明できますか。
8は4の2倍だから、0.5を2倍して1になると思いました。
8回を基にすると、4回が0.5倍になるんだから、8の下に1を書かないといけないと思います。
なるほど。基にする回数を1と見るのですね。
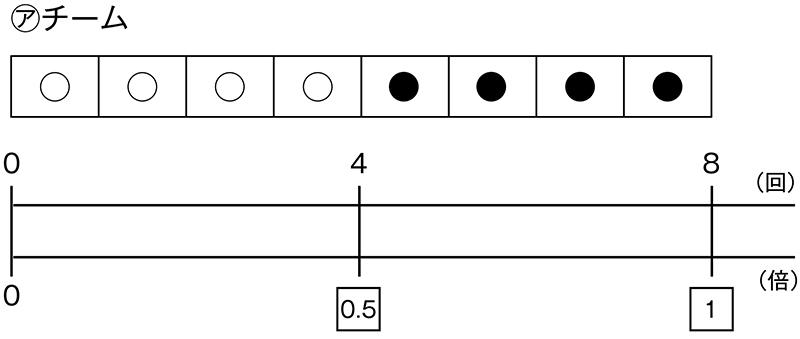
この数直線はシュートした回数を1と見ると、入った数が0.5に当たることを表していますね。ところで、さっきから0.5倍、0.5倍と言ってますが、0.5は4と8から計算で求めることはできますか。
4÷8を計算すれば0.5になります。
入った数の4をシュートした回数の8で割ると、入った数がシュートした数の0.5倍であることが求められるんですね。これで㋐チームについては図でも式でも表せました。次に、㋒チームと㋓チームは半分入った㋐チームより、よく入っていると言えますか。
㋒チームは10回シュートして8回入っています。10回の半分の5回より多く入っています。
㋓チームは12回シュートして9回入っています。12回の半分の6回より多く入っています。
どちらも半分より多く入っていることは分かりました。それでは、㋒チームと㋓チームについて、どちらがよく入っているか、比べ方を考えて、ノートに書いてみましょう。
自力解決の様子
A つまずいている子
入っていない数の差で比べている。
㋒チーム 10-8=2
㋓チーム 12-9=3
答え ㋒チーム
B 素朴に解いている子
シュートした数を最小公倍数でそろえて比べている。
㋒チーム 10×6=60(シュートした数)
8×6=48(入った数)
㋓チーム 12×5=60(シュートした数)
9×5=40(入った数)
答え ㋒チーム
C ねらい通り解いている子
シュートした数を1にそろえて比べている。
㋒チーム 8÷10=0.8
㋓チーム 9÷12=0.75
答え ㋒チーム
学び合いの計画
自力解決のときに、1人1台端末を活用して、自分の考えをクラス内で共有できるようにしておくことで、互いの解決方法を見合いながら、さまざまな解決方法に気付いたり、実際に試したりできるようにしておきます。
イラスト/横井智美

