小5算数「変わり方」指導アイデア《伴って変わる2つの数量の比例関係》
執筆/福岡教育大学附属福岡小学校教諭・田中智史
監修/文部科学省教科調査官・笠井健一
福岡教育大学教授・清水紀宏
単元の展開
第1時 伴って変わる2つの数量の変わり方を調べ、変わり方の違いを話し合う。
▼
第2時(本時)伴って変わる2つの数量の変わり方を表や図に表し、2量の関係が比例かどうかを話し合う。
本時のねらい
伴って変わる2つの数量を見出して、それらの関係に着目し、表を用いて、比例しているかどうかを判断することができる。
評価規準
伴って変わる2つの数量の変わり方を調べて表や図に整理し、着目した数や変わり方を明確にして、比例関係である根拠を説明することができる。(思考・判断・表現)

直方体のたては4㎝、横は5㎝と決めて、高さを1㎝、2㎝、3㎝……、と変えていきます。直方体の体積は、高さに比例しますか。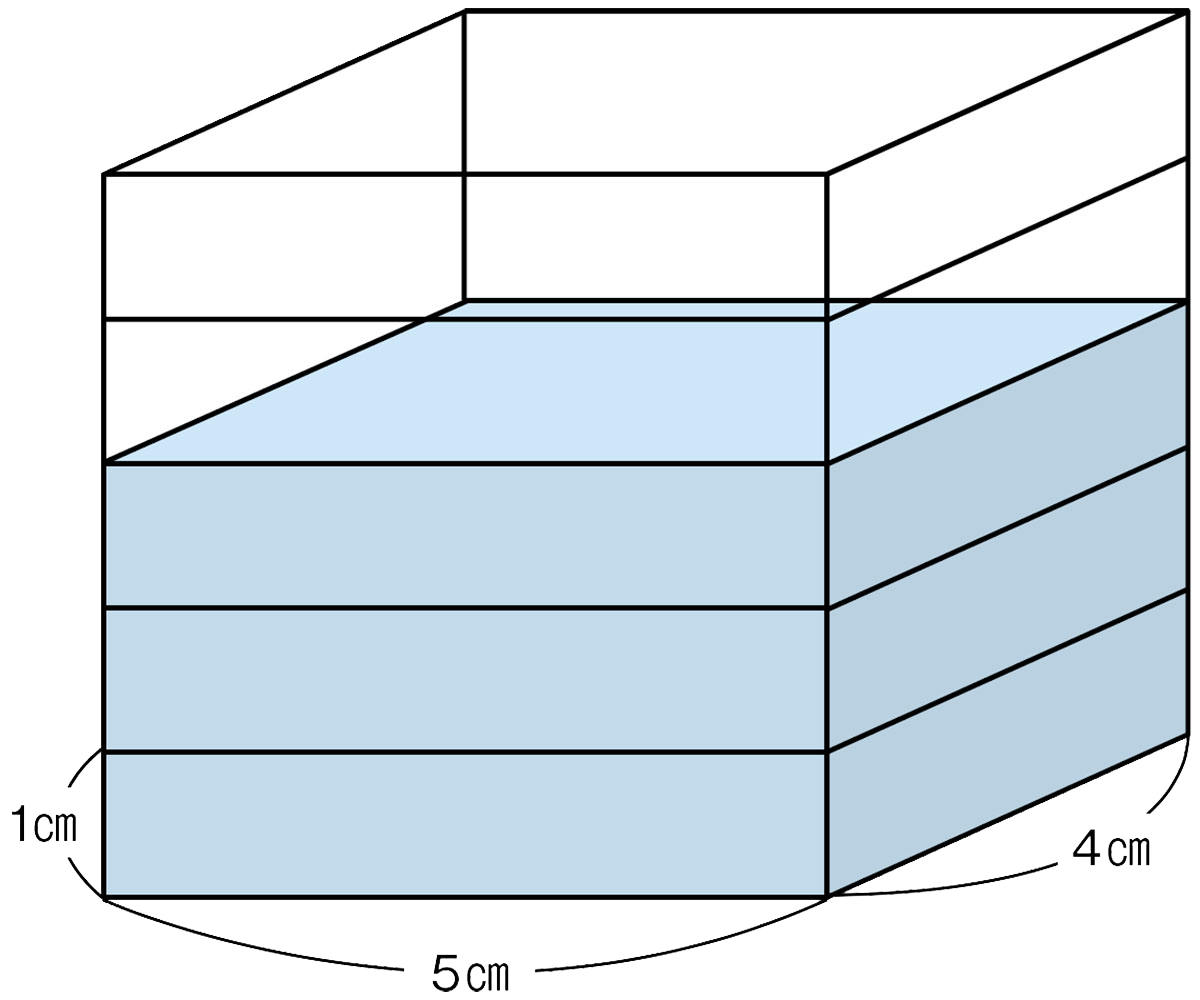
(問題の1文だけを提示して)
高さを変えていくと、ほかに何か変わりますか。
縦と横は決まっているから変わりません。
ほかに変わるものはないのではないかな。
体積が変わると思います。
確かに、高さが変わると体積も変わるな。
この2つの関係は比例している気がする。
私は比例していないと思うな。
意見が分かれていますね。どうすれば解決できますか。
いくつか調べて、表に整理すれば分かると思います。
比例しているかどうかを話し合いたいです。
※ただ問題を提示するのではなく、伴って変わる2量を見付けたり、その関係に対する問いを見出したりすることが、できるようにすることが大切です。
見通し
- 変わり方を調べて表にする。
- 数字を囲んだり矢印をかいたりする。
- 図に整理する。
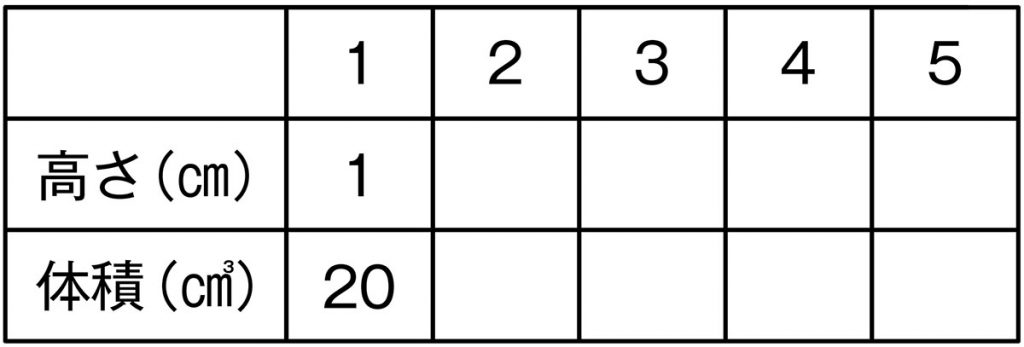
表に整理して、比例しているかどうかが分かっただけでは、ほかの人は納得できないかもしれませんよ。
どこが2倍、3倍になっているかが分かるように説明すればいいと思います。
表の数字を囲んだり、矢印をかいたりしたいです。
僕は図を使って説明したいです。
みんながなるほどと思う説明ができるとよいですね。
※いくつかの場合を調べて表に整理するという方法の見通しは、変化の規則性を見出すうえで大切な方法であるため、全体で共有します。変化の規則性を見出した後は、表にかきこんで着目した数字や関係を明確にしたり、ほかの図に表したり、式にしたりして、自分の思考過程をそれぞれの方法で表現することができるようにしておくことも大切です。

比例しているかどうかを調べて、友達にも分かるように説明しよう。
自力解決の様子
A つまずいている子
いくつかの場合を調べて、表に記述することはできているが、変化の規則性を見出すことはできていない。
B 素朴に解いている子
比例しているかどうかを正しく判断することができており、着目した数や関係に印を付けることができている。
C ねらい通り解いている子
比例しているかどうかを正しく判断することができており、根拠をもって、比例の関係を捉えている。
学び合いの計画
本時では、多くの子供が表を完成するところまではできると想定されます。そこで、表のどこにどのような印を書き加えたか、その印と説明をどのように関連付けたかという視点で、他者の方法に触れることができるような少人数交流が有効です。近くの友達と3人程度のグループになり、互いの表を見せ合って違いを交流したり、説明をし合ったりする交流がよいでしょう。
イラスト/横井智美


