小5算数「整数の性質」指導アイデア《公倍数の性質を理解し、効率的に求めよう》
執筆/埼玉県公立小学校教諭・清水武蔵
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
本時の位置6/12
ねらい
2つの数の公倍数は、最小公倍数の倍数になっていることを理解し、2つの数の公倍数を求めることができる。
評価規準
・公倍数の意味や性質などに着目し、公倍数の求め方を考え、説明している。
・2つの数の最小公倍数を活用し、公倍数を求めることができる。
問題場面
4と6の公倍数を小さい方から5つ求めましょう。どのように見つけたらよいでしょうか。
「4と6の公倍数」というのは、どういう数のことでしたか。
4と6の共通な倍数を公倍数と言いました。
公倍数のうちで1番小さい数が最小公倍数です。
公倍数はどのように求めましたか。
数直線で求めることができました。
それぞれの倍数を書き出して共通の数で求めました。
本時の学習のねらい
数直線や倍数を書き出さなくてもできる公倍数の見付け方を考えよう。
見通し
どんな方法がありそうですか。
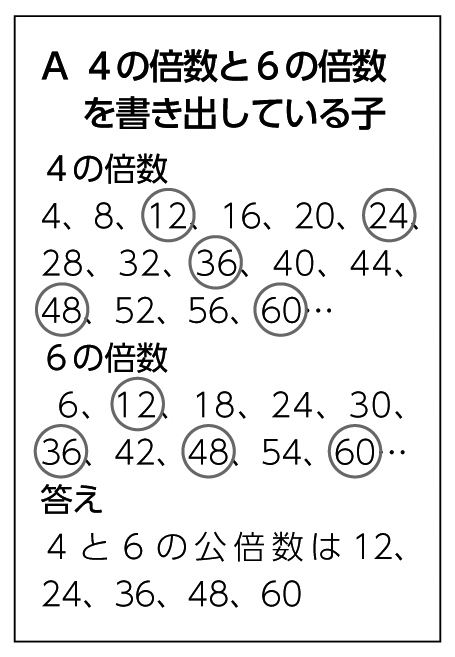
4の倍数と6の倍数をそれぞれ書き出してみようかな。
4の倍数を書き出してその中に6の倍数があるか探してみよう。
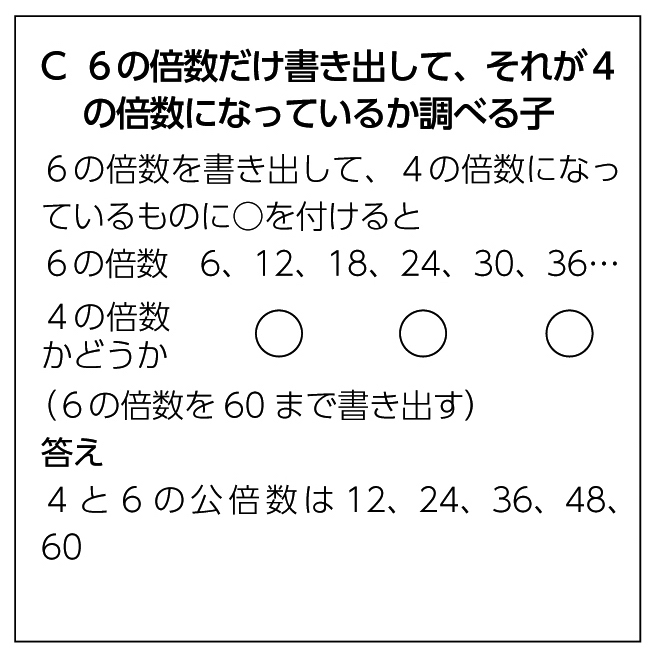
6の倍数を書き出して4の倍数を見付けた方が簡単にできるんじゃないかな。
自力解決の様子

学び合いの学習
3つの考え方の中で、Aの児童が多いことが考えられます。自力解決後の学び合いでは、児童が多様な考え方に触れること、それにより自分の考えを見直すことをねらいに、3~4人組で学び合いを行います。その際、考え方の説明や相違点を中心に話し合いをさせるとともに、それぞれの考え方のよさを話し合えるとよいでしょう。
イラスト/横井智美
『教育技術 小五小六』 2020年9月号より

