小5算数「割合」指導アイデア《シュート成功率で学ぶ割合の概念》
執筆/東京都公立小学校教諭・河内麻衣子
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 1/12時間
ねらい
割合の意味を理解し、比較量と基準量から割合を求めることができる。

評価規準
数量を比べるときに、全体を1とみて部分の大きさを表して比べる方法を考え、説明している。
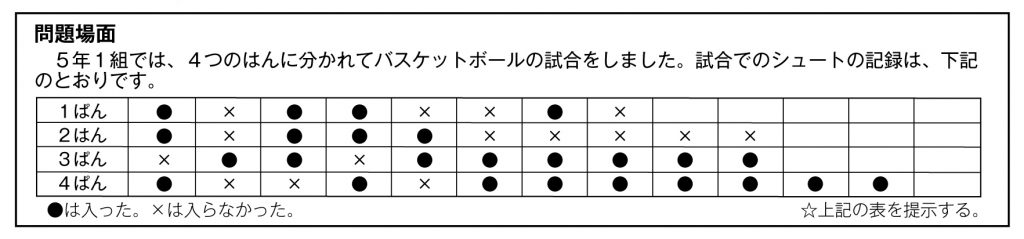
どの班が一番よく入ったと言えるでしょうか。
シュートが入らなかった数だけ見ると、一番少ないのは3班だ。
(入った数、入らなかった数に着目している。)
シュートが入った数だけ見ると、一番よく入った班は4班だ。
シュートをした数が同じ班は2班と3班で、他の班は数が違う。
(シュートした数が同じことに着目している。)
このままでは、どの班が一番よく入ったか比べられないね。
2班と3班は比べられる。
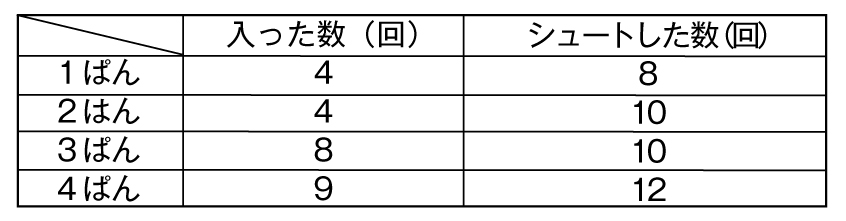
この中で、すぐに比べられる班はありますか。
2班と3班です。
シュートした数が同じだから、入った数で比べればよいので、3班がよく入ったと言えます。
それなら1班と2班は、入った数が同じなので、シュートした数の少ない1班がよく入ったと言えます。
では、1班と3班と4班では、どの班が一番よく入ったと言えますか。
シュートした数が班によって違うので、このままでは比べることはできない。
本時の学習のねらい
入った数もシュートした数もちがうときの比べ方を考えます。
見通し
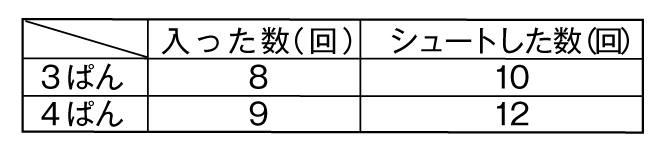
では、この3つの班をどうやって比べますか。
1班はシュートした数に対して半分入ったことになる。
3班と4班はシュートした数に対して半分以上入っている。
3班と4班を比べればよい。
自力解決の様子
Aの考え方
(入っていない数の差で比べる)
3班:10-8=2
4班:12-9=3 3班
Bの考え方
(シュートした数をそろえる)
3班:10×6=60(全体)
8×6=48(回)
4班:12×5=60(全体)
9×5=45(回) 3班
Cの考え方
(シュートした数を1とみる)
3班:8÷10=0.8
4班:9÷12=0.75 3班
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』 2020年1月号より