小3算数「三角形」指導アイデア《正三角形を作図する方法》
執 筆/新潟県公立小学校教諭・伊藤 祐輝
編集委員/文部科学省教科調査官・笠井 健一、新潟県公立小学校校長・遠藤 昇
目次
本時のねらいと評価規準
本時7 / 13時
ねらい
正三角形の作図について、等しい3辺を作図する方法を考える活動を通して、適切な用具を用いて正しく作図する方法を説明できる。
評価規準
正三角形は3つの辺の長さが等しいという定義に基づいて、どのような用具を用いて、どのように操作すれば等辺が作図できるかを説明することができる。また、作図したものが確かに等辺になっているかを説明することができる。
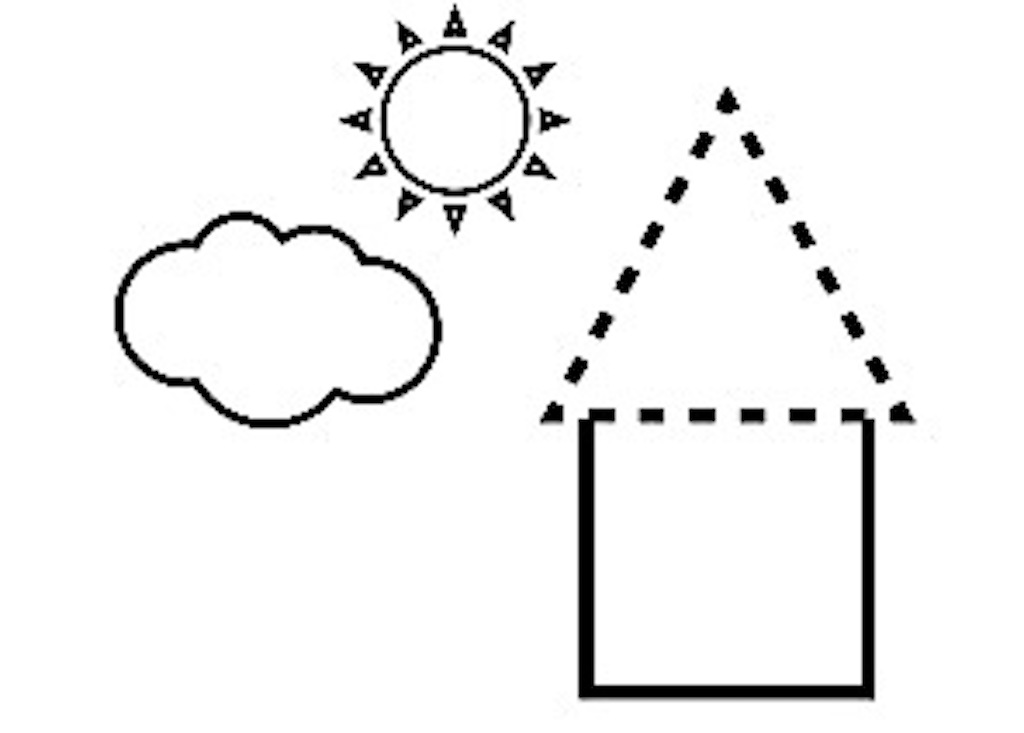
問題
たかしさんは下のような絵をかこうと思っています。 家の屋根を1辺5cmの正確な正三角形にかきたいと思っています。
正確な正三角形とは、どういう三角形のことでしょうか。
辺の長さが3つとも等しい。
少しでも長さが違ってはいけない。
だいたいでよいというわけにはいかない。
このような屋根はよいと言えるでしょうか。
屋根が傾いているからよくない。
辺の長さが違うのが見て分かるから正三角形ではない。
きちんと辺の長さが等しいことを確かめる必要もあるよ。
正確に作図することを意識させるために、正三角形の定義をふり返るとともに、範例を示して正しい作図のイメージをふくらませます。
学習のねらい
1辺が5cmの正三角形を正確にかくには、どうすればよいか。
見通し
まずは定規を使って、5cmの辺を3本かいてみましょう。
線がはみ出てしまうな。
5cmの線3本かいてもうまくつながらない。
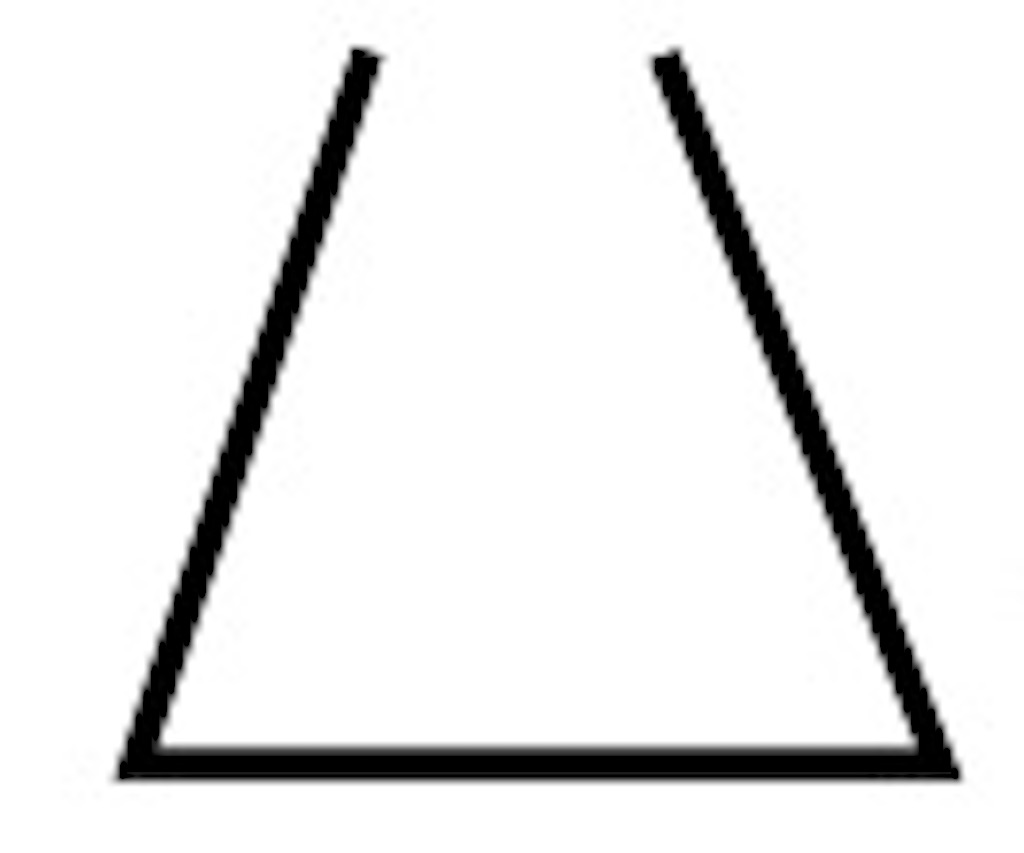
3本の辺がどれも5cmで囲まれるようにかかないといけないよ。
辺と辺の開き具合も考えるといいのかな。
自力解決
A つまずいている子
5cmの辺2本をかいて3本目をかけない。
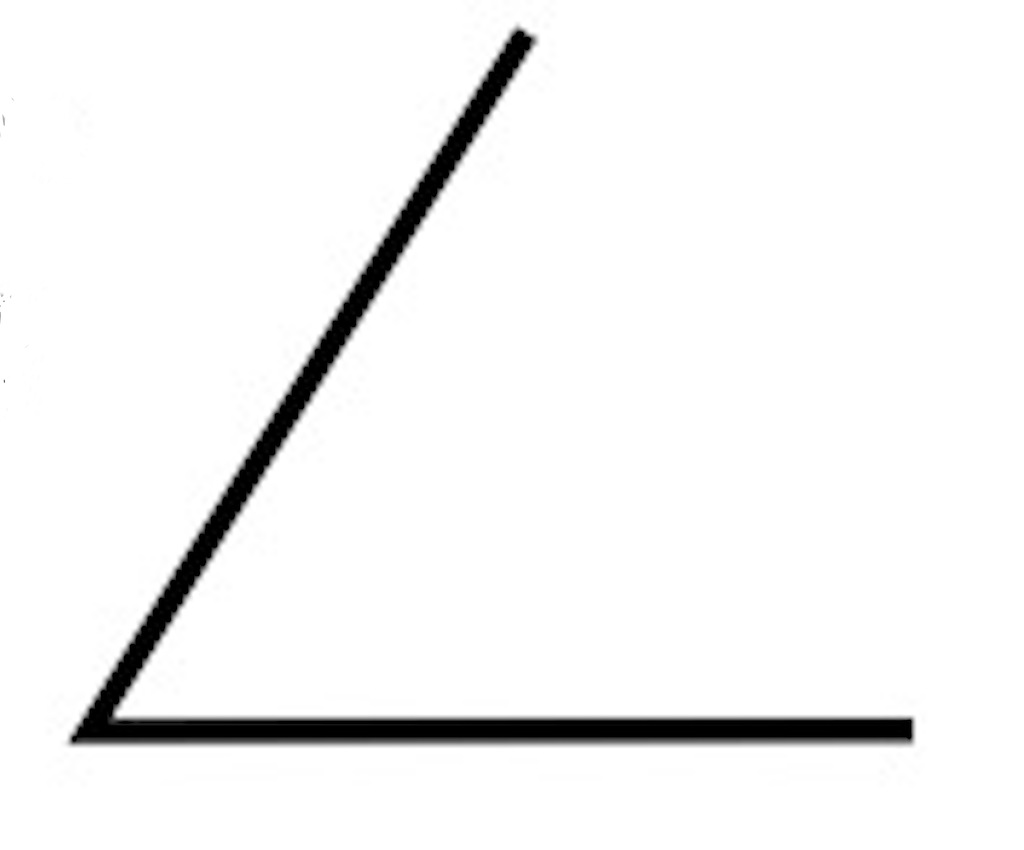
- 結果の見通しがもてない。
B 素朴に解いている子
定規で1辺の両端から5cmの辺2本が交わる点を探す。
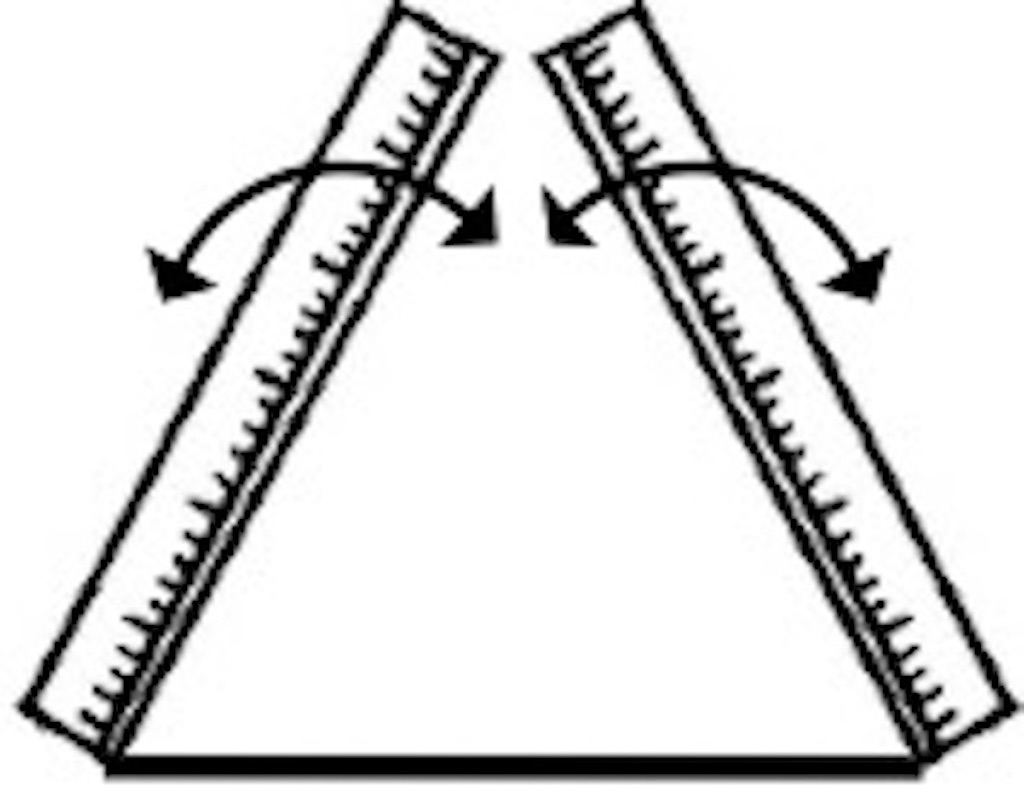
- 3辺がどれも5cmであることを前提として考えている。
C ねらい通り解いている子
コンパスの開きを5cmに固定して、交点を決める。
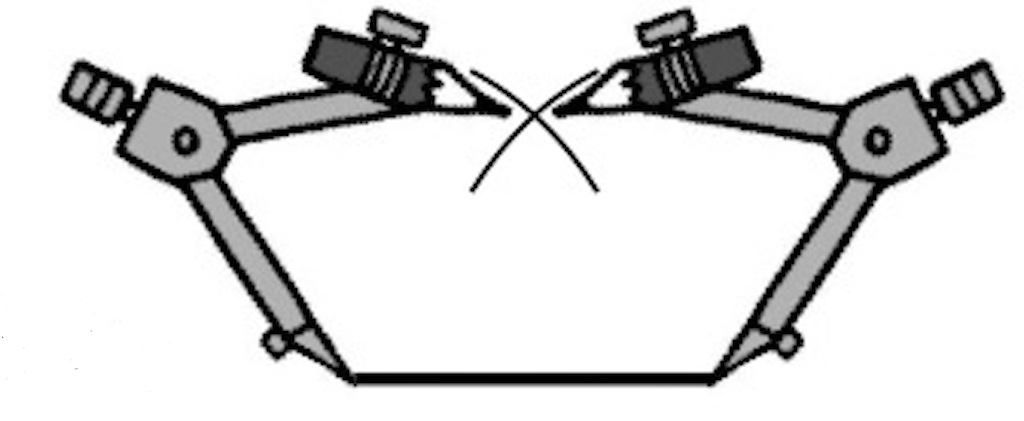
- 頂点の位置を決める方法を同時に探している。
学び合いの計画
イラスト・小沢ヨマ 横井智美
『教育技術 小三小四』2020年1月号より

