小6算数「対称な図形」指導アイデア
執筆／神奈川県公立小学校主幹教諭・八田安史
編集委員／文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥
目次
本時のねらいと評価規準
（本時の位置 2／12 図形の構成と分類）
ねらい
2つの合同な三角形を組み合わせて作った図形を弁別することにより、線対称な図形、点対称な図形を理解する。
評価規準
合同な三角形を重ねるための図形の動かし方について、筋道立てて考えている。(数学的な考え方)
問題場面
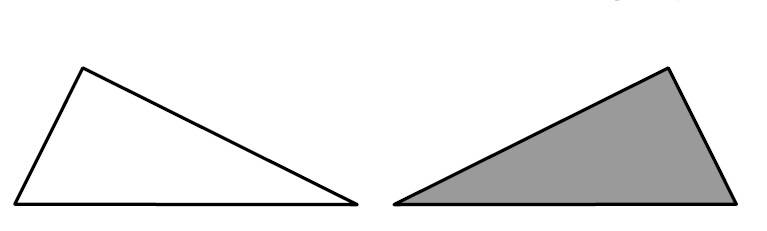
前回、上の表裏で色の違う2 枚の合同な三角形を、対応する辺どうし組み合わせると下のような６つの図形ができましたね。
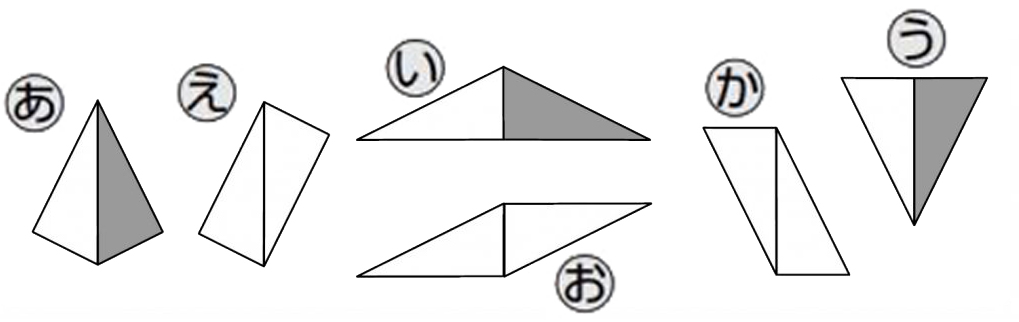
「あ」「い」「う」と「え」「お」「か」に、分けられました。
「あ」「い」「う」は2色でできている。折ったら、ぴったり重なる。
ぴったり重なるというのは、1枚をどのように動かしたら重なったのかな。
くっついている対応する辺を基に、裏返すとぴったり重なりました。
「え」「お」「か」 も、「ずらす」か「回す」か「裏返す」を使って、ぴったり重ねることができるかな。
本時の学習のねらい
「え」「お」「か」は、どのように動かしたらもう一方に重なるか説明しよう。
見通し
「あ」「い」「う」は2色だったけれど、「え」「お」「か」は1色だから裏返さないのかな。
「え」「お」「か」は平行四辺形だから、回せばよさそうだな。
自力解決の様子
Ａ つまずいている子
裏返しにして、しまっている
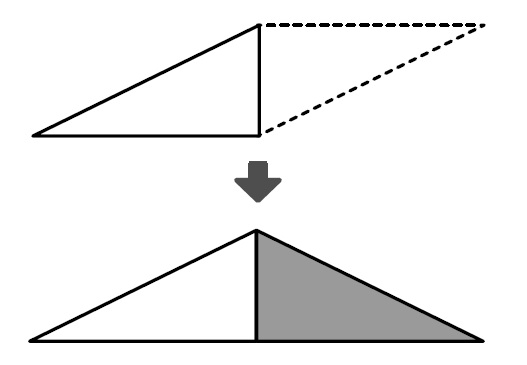
B 素朴に解いている子
ずらしてから、回している
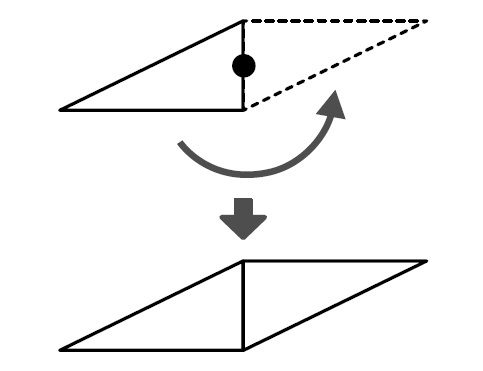
C ねらい通りに解いている子
中心で、回している
学び合いの計画
一年生で「ずらす」「回す」「裏返す」を行っています。前時での線対称の操作を想起し、本時でもよく考えずに裏返してしまう子がいます。自力解決の途中でそのようなアイデアを取り上げ、裏と表の色に着目できるようにします。
イラスト／ 横井智美
『教育技術 小五小六』2019年4月号より
