【中1・数学「反比例のグラフ」】デジタルの特性を活用し反比例のグラフを視覚的に理解〈デジタル×深い学び〉
今回紹介するのは、板橋区立志村第一中学校の数学科授業。自ら構築した「Math box」というオリジナルウェブサイトなどを活用し、自由進度学習を取り入れた授業づくりを行う中村主任教諭による、中学1年生の「反比例のグラフ」の授業レポートをお届けします。

この記事は、連続企画『「デジタル×深い学び」の授業デザインReport』の28回目です。記事一覧はこちら

板橋区立志村第一中学校
教育内容の特色の一つに「ICT社会を生き抜く総合的な学力育成」がある。令和2年度より、板橋区による保幼小接続・小中一貫教育を実践している。
目次
反比例のグラフの形を予想し、確かめる
前時までに反比例の式について学んだ生徒たちは、この日、そのグラフがどのような形になるかを探究しました。まずは「y=[MATH]\(\frac{6}{x}\)[/MATH]」という式をもとに、反比例のグラフがどのような形になるか、想像してみます。
反比例のグラフがどんな形か、ちょっと予想もつかないので、比例のときを思い出しましょう。比例のグラフってどんなんだったっけ?
原点を通る直線。
そう。そのとき、直線になることをどうやって確かめた?
点の集合体。
そうだったね。式にいろんな数字を当てはめて、点を打っていったら「どうやら直線になりそうだ」って分かったよね。だから今回も、まずはそのやり方でやってみましょう。
まずは手作業のアナログな活動からスタート。「xが-6のとき、-3のとき、-2のとき、-1のとき…」「xがゼロの式は成り立たないからバツにしましょう」「xが1のとき、2のとき、3のとき、6のとき…」と計算しながら、手元のプリントに点を打っていきます。
どう? この線をつないでいったらどんなグラフになりそう?
カクカクした線?
曲線?
じゃあ、実際に点を増やしていったらどうなるか、見てみましょう。
中村先生はここで「Math box」から教科書のデジタルコンテンツを投影。画面上で点の密度を上げていくことで、グラフの形が浮かび上がってきます。
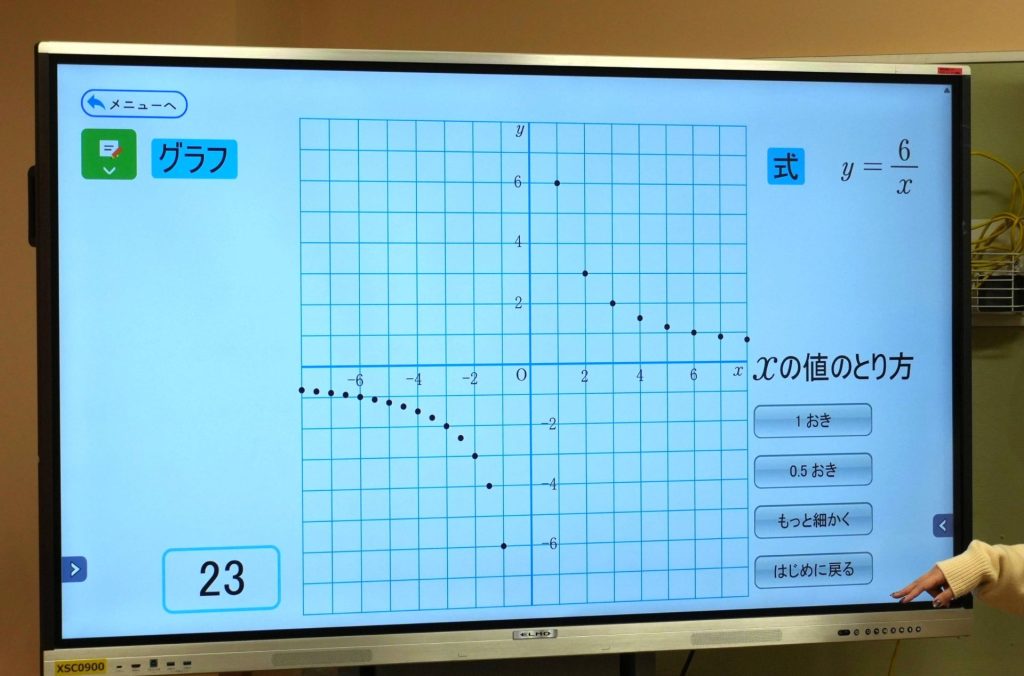
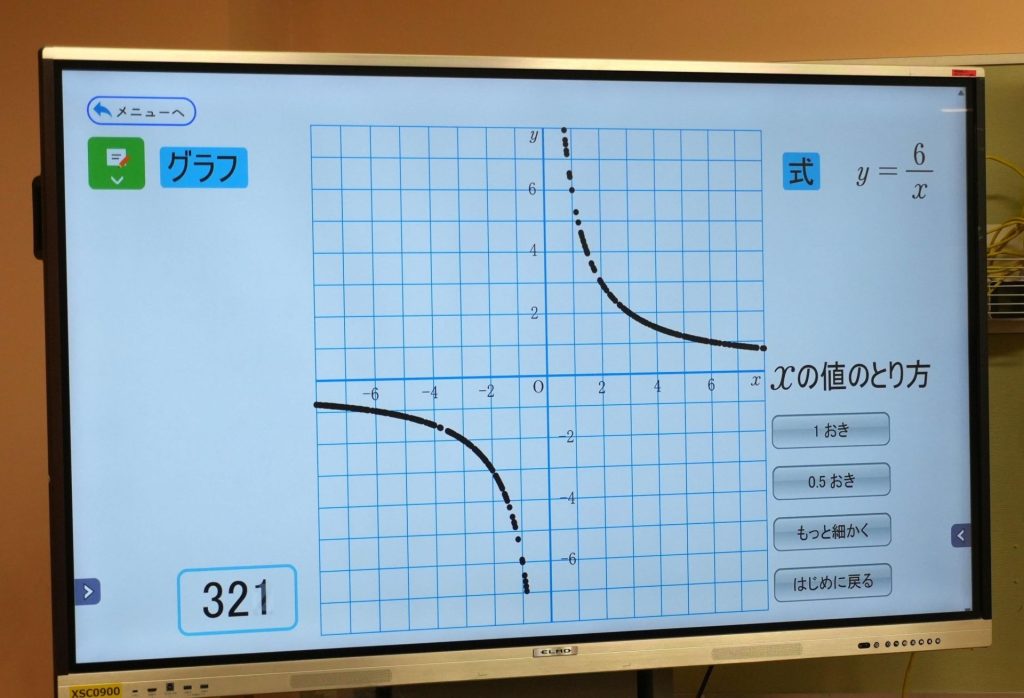
どんな形が見えてきたかな?
原点を通らない、2本の曲線。
そう、反比例のグラフはこのように、2つの曲線がセットになった形で表されます。これを「双曲線」と言います。
●指導のポイント
点を3個、4個打っただけだと、曲線になることが想像できず、点どうしを定規で真っすぐに結んでしまう生徒もいます。デジタルで点を増やしていくことで、グラフが曲線になること、定規では表せないグラフになることが視覚的に分かるので、生徒たちにとっても腑に落ちる解説になったのではないかと思います。
グラフの端がどうなるか、グラフを拡大して確認
反比例のグラフでもうひとつ、悩みどころなのが「グラフの端はどうなるか?」。xの値が変化するにつれてグラフは軸に近づいていくが、最終的に線は軸にくっつくのかどうか? この疑問についても中村先生はまず生徒たちに答えを予想させ、その仮説が正しいかを計算とグラフで確かめていきます。

