小６算数「円の面積」指導アイデア《等積変形で面積を求めた式から求積公式を導き出す》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.08.28

年間指導計画

年間指導計画はこちらをクリック

・対照な図形
・文字を使った式
・場合の数
・分数×÷整数
・円の面積
・分数×分数
・分数÷分数
・角柱と円柱の体積
・資料の調べ方
・小数と分数の計算
・比と比の利用
・拡大図・縮図
・比例と反比例
・およその面積と体積
・算数のまとめ

単元の展開（各時の主な学習活動内容）

第１時　方眼を用いて、半径５㎝の円の面積を求める。
第２時　半径10㎝の円を16等分した扇形を敷き詰め、既習の図形に変形させ、面積を求める。
第３時（本時）前時に等積変形させ、面積を求めたそれぞれの式から、求積公式を導き出す。
第４時　正方形と四分円を組み合わせた形の面積を求める。
第５時　形の概形を基本的な図形と捉えて、面積を概測する方法を理解する。
第６時　円の求積公式を用いて、複合図形の面積を求める。

本時のねらい

円を変形させた既習図形の面積の求め方を基に、円の面積を求める公式を導き出すことができる。

評価規準

図形を構成する要素に着目し、円の面積を求める公式を考えることができる。

本時の教材のポイント

本時では、前時に学習した、円を変形させた平行四辺形や三角形等の面積の求め方を基にして、円の面積を求める公式を導き出します。予想される子供のつまずくポイントは、「①平行四辺形や三角形等の底辺や高さが、円のどの部分と同じであるのか」「②平行四辺形や三角形の面積を求める公式をどのように変形させればよいか」の２点が考えられます。

①についてつまずいている子供には、変形前の円と変形後の図形を並べて提示し、底辺や高さに当たる部分を円のどの部分になるのか色付けしながらなぞることで、同じ部分であることを視覚的に理解できるように支援するとよいでしょう。また、円を細かく分割すればするほど、辺が直線になり正確になっていきますが、細かくし過ぎると底辺が円周の何分の一の長さなのか分からなくなってしまうので注意が必要です（本ページでは、16等分したものを基に考えています）。

②についてつまずいている子供には、①で示した同じ部分の長さを円で用いられる部分の名称（半径、円周率など）に置き換える支援をするとよいでしょう。式を置き換えていく際、換わった部分を色分けするなど、平行四辺形や三角形などの公式が、円で用いられる部分の名称だけで表されていく様子をていねいに示していくとよいでしょう。

どちらの場合も、苦手な子供にとっては苦しい時間になることが予想されます。また、前時で平行四辺形、三角形、台形など、多くの既習図形が提示された場合、式が乱立して混乱を招くかもしれません。同じ既習図形で考えた子供でグルーピングし、協働的に解決に向かわせる学習形態の工夫も有効です。

本時の展開

前回は、円を平行四辺形や三角形などの図形に変形して、円の面積を求めました。それぞれの面積の求め方を確認しましょう。

（Ａさん）　私は、平行四辺形に変形して考えました。すると、面積＝底辺×高さで求めることができました。

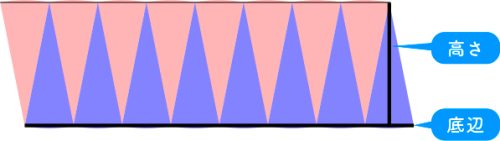
（Ｂさん）　僕は、三角形に変形して考えました。すると、面積＝底辺×高さ÷２で求めることができました。

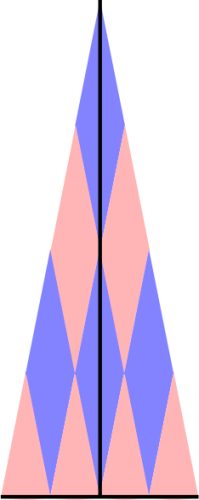
（Ｃさん）　私は、台形に変形して考えました。すると、面積＝（上底＋下底）×高さ÷２で求めることができました。

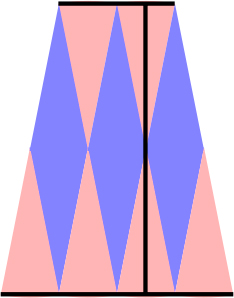
みなさん、円の面積の求め方を習った図形に変形して円の面積を求められましたね。ここまでできているなら、円の面積を求める公式をつくることができますね。

えっ!?　どうするのですか。

３人とも違う図形に変形させているから、公式もバラバラになってしまうのではないですか。

どうすれば、円の面積を求める公式をつくれるのだろう。

円の面積を求める公式を考えよう。

平行四辺形や三角形の面積の求め方を基に、円の面積を求める公式を考えよう。

見通し

底辺や高さが円のどの部分になるのか、形を戻してみよう。

底辺や高さと同じ部分を、変形前の円に色を塗って確かめてみよう。

底辺や高さと同じ長さを、半径や円周に置き換えてみよう。

自力解決の様子

Ａ　つまずいている子

・底辺や高さが、円のどの部分と等しいか理解できない。

Ｂ　素朴に解いている子

・底辺や高さを、半径や円周という言葉に置き換えることができる。

・前時で自分が変形させた図形においてのみ、円の面積を求める公式を導き出すことができる。

Ｃ　ねらい通り解いている子

・底辺や高さを、半径や円周率という言葉にスムーズに置き換えることができる。

・自分で変形させた図形以外のその他の既習図形の面積を求める公式からも、円の面積を求める公式を導き出すことができる。

全体発表とそれぞれの考えの関連付け

みなさん、円の面積を求める公式はつくれましたか。Ａさんは平行四辺形で考えていましたね。

（Ａさん）　私は、平行四辺形の底辺と高さが、円のどの部分と等しくなるのか形を戻して調べ直すことにしました。すると、底辺の長さは、１つの扇形の弧の長さ８つ分だから、円の円周の半分の長さと等しくなることが分かりました。また、高さの長さは円の半径の長さと等しくなることが分かりました。

なるほど。形を元に戻して、同じ部分に色を塗って確かめたのですね。

（Ａさん）　はい。等しくなる部分が分かったので、平行四辺形の面積を求める公式に当てはめてみました。すると、底辺×高さ＝円周の長さの半分×半径と表すことができました。

つまり、円の面積を求める公式は、円周の長さの半分×半径になります。

円に使われる言葉を使って表すことができましたね。この式を見て、他のみなさんは気になるところはありませんか。

「の半分」という言葉は、「÷２」と表すことができそうです。

（Ａさん）　確かにそうですね。では、円周の長さ÷２×半径でいいですか。

円周の長さを求める公式もありました。その部分も直せないですか。

（Ａさん）　円周の長さは、直径×円周率だったから、直径×円周率÷２×半径になります。これ以上は直せそうにないです。

この式を使って、実際に問題を解く場面を想像してみましょう。この公式を使うと、直径と半径の両方の長さを求めることになりそうですね。

それは二度手間です。どちらか１つが分かれば、もう一方の長さが分かるのだから、どちらか１つの言葉で表せるのではないですか。

あっ！　直径×円周率÷２×半径の「直径」と「÷２」を計算すると、「半径」になるよ。これを使って式をつくり直すとどうなるかな。

（Ａさん）　円の面積＝半径×半径×円周率になりました。

すごい！　とってもすっきりした形になりました。

平行四辺形の面積を求める公式から、円の面積を求める公式がつくれましたね。他の図形で考えたみなさんは、どうなりましたか。

（Ｂさん）　僕は三角形の面積を求める公式を使って求めました。底辺は１つの扇形の弧の長さ４つ分だから、円の円周の長さの、[MATH]\(\frac{1}{4}\)[/MATH]と等しくなります。また、高さは、半径の４倍の長さと等しくなります。だから、底辺×高さ÷２＝（円周の長さ÷４）×（半径×４）÷２と表せます。

これまで話し合ってきたことを使いながら円の面積を求める公式をつくってみると、

直径×円周率÷４×半径×４÷２＝直径×円周率÷４×半径×２＝直径÷２×円周率×半径＝半径×円周率×半径

となり、僕も、円の面積＝半径×半径×円周率になりました。

底辺や高さが平行四辺形のときと違っていても、同じ公式ができあがったのですね。では、台形で考えた人はどうなりましたか。

（Ｃさん）　はい。台形の場合は、上底＋下底は１つの扇形の弧の長さ８つ分だから、円の円周の長さの半分と等しくなります。また、高さは、半径の２倍と等しくなります。だから、（上底＋下底）×高さ÷２＝（円周の長さ÷２）×（半径×２）÷２と表せます。

これまでと同じように円の面積を求める公式をつくってみると、

直径×円周率÷２×半径×２÷２＝半径×円周率×半径×２÷２

となり、×２÷２はそれぞれ１になるから、私も円の面積＝半径×半径×円周率になりました。

どの図形に変形して考えても、円の面積を求める公式は、「半径×半径×円周率」になりましたね。底辺や高さを円の半径や円周の長さと結び付けながら、円の面積を求める公式を求めることができましたね。

私たちでつくった公式だから、絶対に忘れないです。

僕たちでつくった公式を早く問題で使って解いてみたいです。

それでは、公式を使って問題を解いてみましょう。

まとめ

円の面積＝半径×半径×円周率で求めることができる。

評価問題

次の図形の面積を求めましょう。

子供に期待する解答の具体例

①式３×３×3.14＝28.26　28.26㎠

②式 10÷２＝５
５×５×3.14＝78.5　78.5㎠

感想例

平行四辺形や三角形の面積を求める公式が、円の面積を求める公式に変わるなんて驚きました。
円を等分して平行四辺形などに形を変えて面積を考えたけれど、今日、それを元に戻して円の面積を求める公式をつくることができました。違う形だけど、つながっている感じがして面白かったです。
平行四辺形や三角形の面積を求める公式を基に、底辺や高さを半径や円周の長さに置き換えて円の面積を求める公式につくりかえることができました。三角形や台形の底辺や高さや公式はそれぞれ違うけれど、置き換えて計算していくうちにどれも「半径×半径×円周率」になったので不思議でした。