小5算数「□と△を使った式」指導アイデア《伴って変わる2つの数量の関係に着目し、問題を解決する》
執筆/横浜市立桜岡小学校教諭・吉田道
監修/文部科学省教科調査官・笠井健一
島根県立大学教授・齊藤一弥

目次
単元の展開
第1時(本時)伴って変わる2つの数量の関係に着目し、問題を解決する。
本時のねらい
伴って変わる2つの数量の関係を表や図、式に表して問題解決の方法を説明することができる。
評価規準
伴って変わる2つの数量を見いだして、それらの関係に着目し、表や式、図を用いて、それらの関係を表現し、問題解決の方法を説明している。
本時の展開

正方形が30個のときのぼうの数の求め方を説明しよう。
長さの等しい棒で、このように正方形をつくり、横に並べていきます。
1つできました。
このとき棒は何本いりますか。
4本です。
では、正方形を増やしてきますよ。(2個、3個、4個と黒板に棒を張り、正方形を増やしていく)
正方形が2個だと7本だ。
3個だと10本だよ。
4個だと13本だ。
正方形が30個並んでいるようにしたいのですが、棒は何本必要ですか。
実際に並べたら分かるな。
30個は多いな。
黒板に並び切らないかもしれないな。
ノートに図としてかけるよ。
並べるよりも、もっといいやり方があります。
「比例」の学習で、表で調べました。
式もつくれます。
比例では伴って変わる量がありましたね。この問題でもありますか。
正方形の数と棒の数です。
正方形の数と棒の数がどのように増えるのか、きまりを見付ければよいと思います。
そうですか。では、今日の学習はどんなことに気を付けて進めますか。
「正方形の数と棒の数の関係に気を付けて、正方形が30個のときの棒の数の求め方を説明しよう」はどうですか。

正方形の数と棒の数の関係に着目して、棒の数の求め方を説明することができる。
見通し
図をかいていくと棒の数が分かりそう。(方法の見通し)
表に表すと2つの量の関係が分かりそう。(方法の見通し)
2つの量の関係を見付けて式にできそう。(結果の見通し)
自力解決の様子
A つまずいている子
・正方形は4本でできる。だから、正方形30個分と考え、120本としている。
・増えた分のまとまりの3本を見付けることができず、どのように解いてよいのか分からない。
B 素朴に解いている子
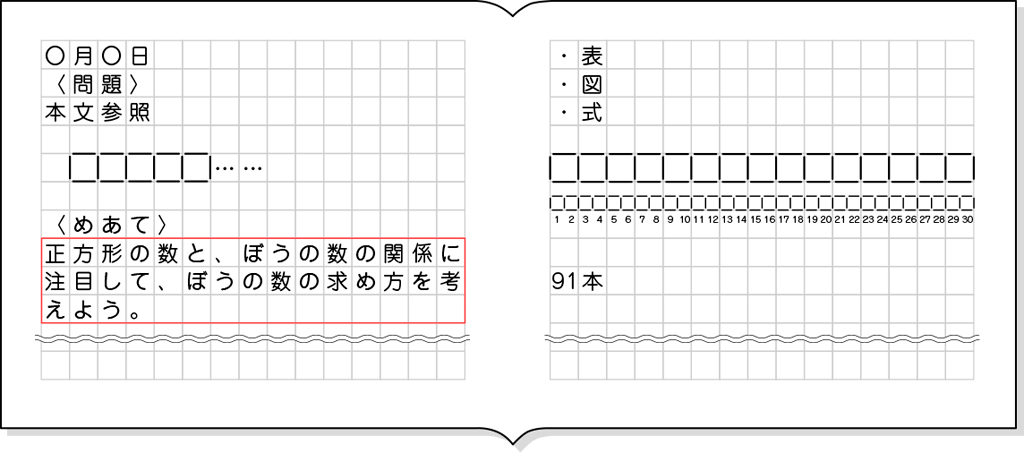
・□が30個のときの図をかいて、1本ずつ数えて求めている。
・表を書いて、正方形が30個のときの棒の本数を求めている。
C ねらい通り解いている子
・表や図をかいて、正方形30個とするために、左の正方形に「コの字」を30個より1少ない29個加えればよいことを理解できている。
・左端の1本に「コの字」を3本ずつ増やすことを表や図で表し、式で表現することができている。
学び合いの計画
本学習は、加法と乗法を用いて表される2つの数量の関係を扱い、その変化や対応の特徴を考察することにより、これまでの2つの数量の関係の考察の仕方と統合的に捉えることになります。
そこで本時の学習では、正方形の数が1増えると、棒の数がいくつ増えるのかということについて、表や図に整理しての変化の様子を捉えることにより、既習の2つの数量の関係の考察の仕方について帰着して考えていきましょう。まず、伴って変わる2つの数量が何と何であるのか見いだすことを大切にします。表を用いる際にも、項目についてよく考え、それぞれの数量を明らかにして数量の変化や対応の特徴に目を向けていくようにしていき、□や〇を用いた式に表し、一方の数量が大きくなったときでも、もう一方の数量を計算で簡単に求めることができるよさにも気づかせます。その後、正方形の数を50個の問題を同様に考え、すべての子供が概ね正しく立式できるようにしましょう。
自力解決や考えの共有の場面では、1人1台端末の活用が有効となります。自他の解決方法を共有できるようにし、互いの解決方法を見合うことができるようにしておくと、Aの子供は、問題解決の方法と、その説明の仕方を確認することができ、BやCの子供は、他の方法に触れることで、自分の方法との共通点や相違点を考えることが期待できます。考えの共有の場面では、何を基にして数量が変わっていくかを明確にするため、言葉による説明だけでなく、図や表にある基にする数量と式にある変化する数量を対応させ、色を変えたりマーキングしたりして、注目しやすくする工夫ができます。
ノート例
A つまずいている子
B 素朴に解いている子
全体発表とそれぞれの考えの関連付け
※C1、C2、C3のそれぞれが発表をする。
C1〈図で説明する子供〉
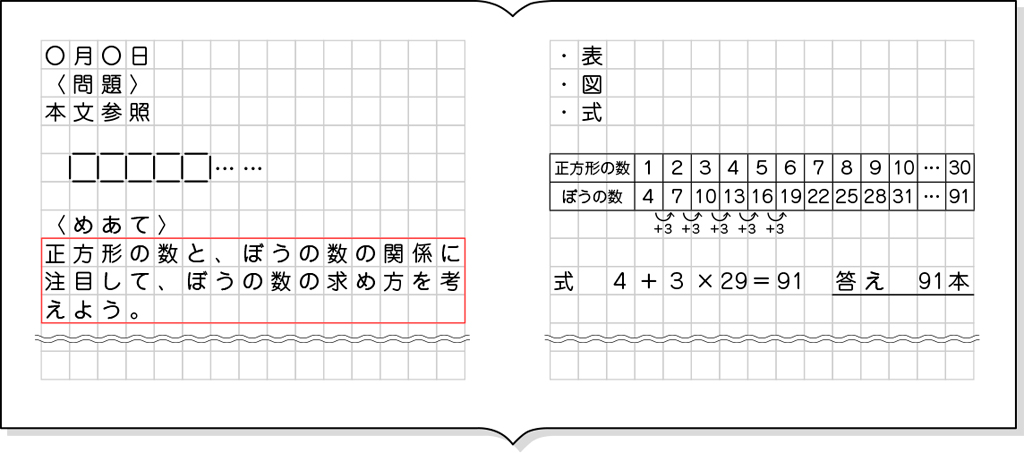
正方形のところが4本です。コの字が3本ずつ、1、2…と全部で29個あるから、3×29=87。87本です。合わせると4+87で91本です。式にすると4+3×29=91になります。
C2〈図で説明する子供〉
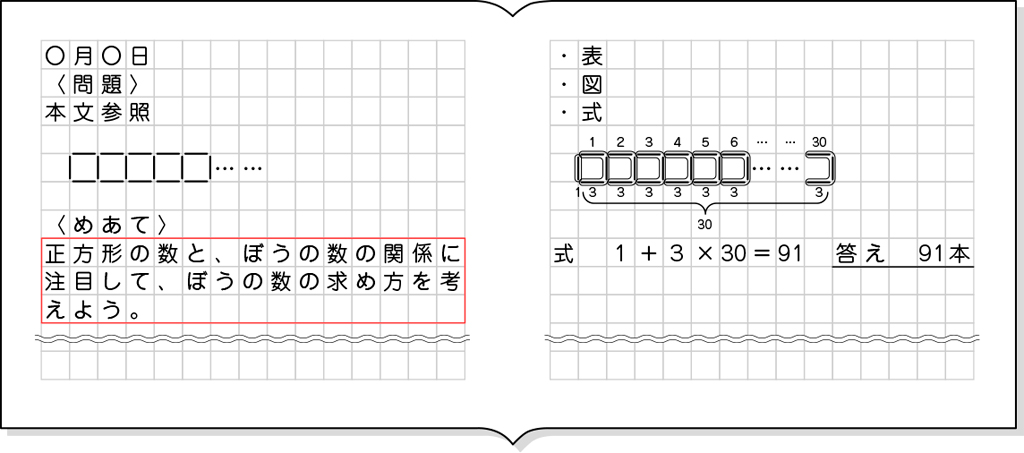
正方形が30個あります。すべての正方形にコの字があります。3本ずつ30個あるから、3×30=90で90本です。でも、最初の1つの正方形にはあと1本棒があるので、合わせると90とはじめの1で91本です。式にすると、1+3×30=91になります。
C3〈表で説明する子供〉
正方形が1つで4本です。そこから正方形を1つずつ増やしていくと、棒の数が3本ずつ増えていきます。増える回数は全部で29回あるから、3×29=87で、87本です。合わせると、4+87で91本です。式にすると、4+3×29=91になります。
3つを見比べて、似ているところはありますか。
イラスト/横井智美

