小５算数「面積」指導アイデア《ひし形の面積の求め方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.01.29

単元の展開

第１時　平行四辺形の面積の求め方を考え、説明することができる。
▼
第２時　平行四辺形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第３時　高さが平行四辺形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
▼
第４時　三角形の面積の求め方を考え、説明することができる。
▼
第５時　三角形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第６時　高さが三角形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
▼
第７時　台形の面積の求め方を考え、説明することができる。
▼
第８時　台形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第９時（本時）ひし形の面積の求め方を考え、説明することができる。また、ひし形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第10時　学習の定着を確認する。

本時のねらい

前時までの平行四辺形、三角形、台形の面積の求め方を考える過程において働かせてきた「既習の形に帰着する」という見方・考え方を生かして、ひし形の面積を求める公式を考え、筋道立てて説明することができる。

評価規準

等積変形、倍積変形、分割してできた既習の形の辺の長さとひし形の対角線の長さに着目し、ひし形の面積の公式を考え、説明している。

本時の展開

ひし形の面積の求め方を今までに学習してきた求積方法を使って説明しよう。

これは何という図形ですか。

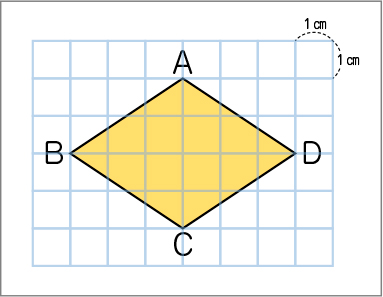
ひし形です。

横に倒すと平行四辺形にも見えるよ。

平行四辺形のように向かい合っている２組の辺は平行ではあるんだけど……もっとなんか……。

もっと条件があるってことかな。それは４つの辺の長さが等しいということだよ。

さらに、２本の対角線が垂直に交わるからひし形なんだよ。

なるほど。平行四辺形のなかに、ひし形という形があるということですね。それでは、このひし形の面積もみんなは求められそうですか。

できます。

今まで学習した図形のように、切ったり変形したりすればできそうだね。

使った長さを言葉にしたら公式にもできるね。

２つの三角形に分ければできるよ。

大きな長方形にしてから半分にすればできるよ。

切ってから移動して、長方形にするとできるよ。

求め方を図や式で表してみましょう。

「既習の形に帰着する」という見方・考え方を生かして、ひし形の面積を求める公式を考え、筋道立てて説明することができる。

見通し

図形を切ったらできそうだな。（方法の見通し）

公式を知っている図形に形を変えたらできそうだな。（方法の見通し）

ひし形でも、どこかに着目すると公式をつくれそうだな。（結果の見通し）

自力解決の様子

A　つまずいている子
｢既習の形に帰着する」という見方・考え方を働かせることができずにいる。

Ｂ　素朴に解いている子
分割、等積変形、倍積変形のどれか１つの考え方を使って、ひし形の面積を求積している。

Ｃ　ねらい通り解いている子
分割、等積変形、倍積変形それぞれの考え方で着目している構成要素に気付き、公式をつくり出している。

学び合いの計画

本学習は、三角形や平行四辺形、ひし形及び台形の面積について、構成要素に着目して、分割や等積変形、倍積変形という考え方を使って既習の形に帰着し、計算で求められると理解することが大切です。また、公式を用いて面積を求めることをゴールにするのではなく、図形の構成要素のどこに着目すれば、いつでも求積することができるのかを単元を通して気付いていけるようにします。

そこで、本時の学習では、単にひし形の面積を求めることに終始するのでなく、それぞれの考え方を比較し、対角線に着目することで公式をつくり出します。そして、平行四辺形の求積方法をふり返りながら、対角線を用いることの便利さに気付かせましょう。さらに、アプリ「GeoGebra」を用いて、ひし形の対角線を動かし、たこ形に変形する様子を視覚的に示すことで、対角線の便利さを感じてほしいです。

第６学年で学ぶ「円の面積」の求積にもつながるように、分かったことや着目した構成要素を学習の途中でふり返って整理しながら発展的に考える意欲を醸成していくことが大切です。学び合いの後半で、ひし形とたこ形を比較するときに１人１台端末の活用が有効となります。２つの対角線同士が直交する関係のまま形が変形することを実感できるからです。このように図形の学習をする際には、動的に示すことが有効です。

ノート例

Ａ　つまずいている子

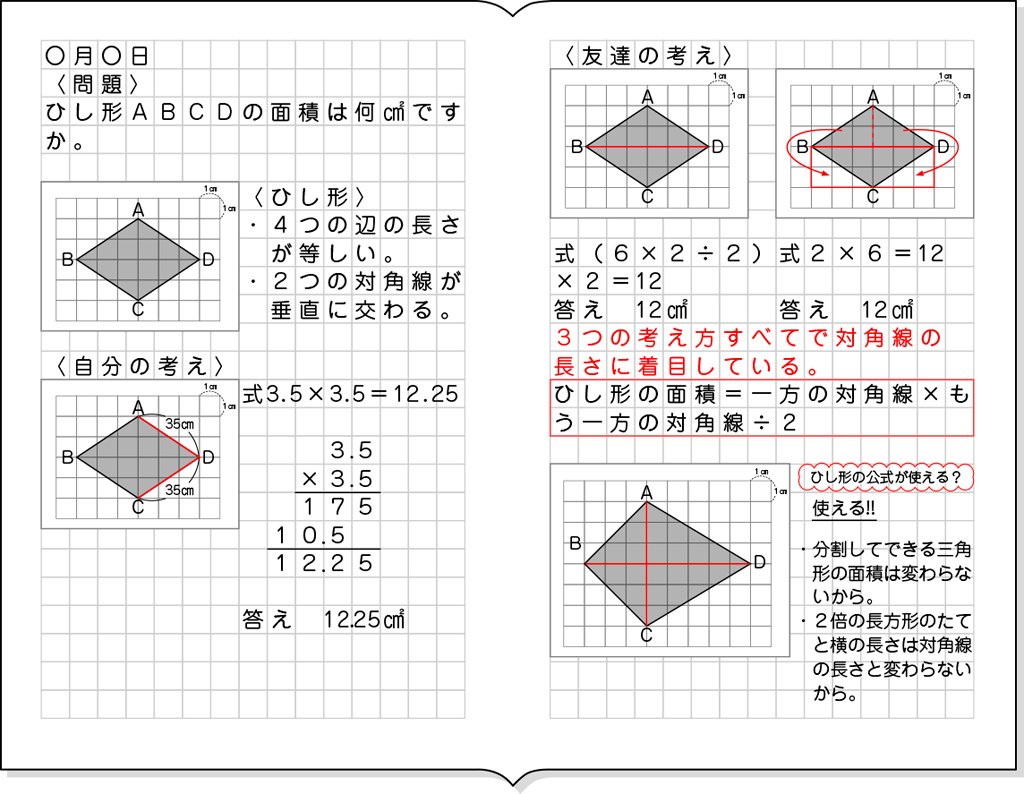
Ｂ　素朴に解いている子

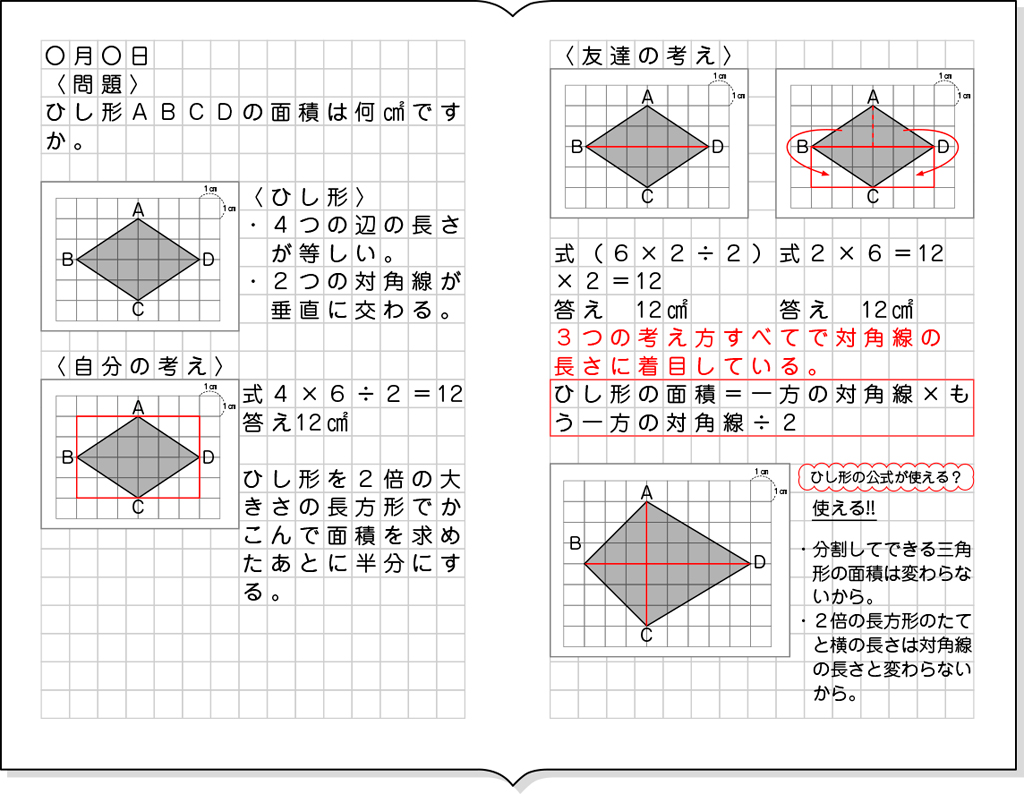
全体発表とそれぞれの考えの関連付け

※Ｃ１、Ｃ２、Ｃ３のそれぞれが発表をする。

Ｃ１
２つの三角形に分けて､（６×２÷２）×２で求められるよ。

Ｃ２
長方形の半分と見て､（４×６）÷２で求められるよ。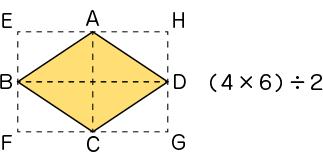

Ｃ３
長方形に形を変えて､（４÷２）×６で求められるよ。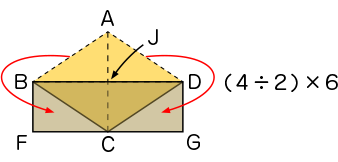

３つの考えを見比べてみて、ひし形のどの部分の長さを使って求めていますか。

Ｃ１さんの考えの２つの三角形の底辺は、対角線の長さと同じです。

Ｃ１さんの考えの三角形の高さのところは、ひし形のもう１つの対角線の長さの半分を使っています。

Ｃ２さんの考えは長方形に変形していて、縦の長さも横の長さもひし形の対角線の長さと同じです。

Ｃ３さんの考え方で出てくる長方形の横の長さは、ひし形の対角線の長さで、縦の長さは、もう１つの対角線の半分の長さになっています。

３人の考えはひし形のどの部分に着目して面積を求めていますか。

３人ともそのままの長さだったり、半分の長さだったりはしているけど対角線の長さを使っています。

今まで勉強していた図形では対角線なんて使わなかったけど、ひし形は対角線を使って公式をつくれそうだね。

ひし形も今までの図形と同じように公式をつくることができそうですね。公式をつくりましょう。

Ｃ２さんの考えを言葉の式にして、対角線×対角線÷２になると思う。

Ｃ３さんの考えた（４÷２）×６も４×６÷２とすることもできるから同じだね。

Ｃ１さんの考えた式には４がないけどよいのかな。

Ｃ１さんの考えた（６×２÷２）×２も（　）を外して、６×４÷２にできるから４を使って式にできるね。

みんなは、対角線に着目して公式をつくることができましたね。このひし形なのですが、横に倒すと何に見えたのでしたか。

平行四辺形に見えます。

ということは、ひし形は平行四辺形の公式でも求められるかも。

えっ。でも高さってどうやって測るの。

定規をこう置いて……、うーん、正確に底辺に対して垂直な直線をかくのは難しいな。

それに比べて、対角線同士は必ず直交するから、すぐに測れるね。

やっぱり対角線の長さを使って面積を求めたほうが便利だね。

みんなは対角線の便利さにも気付きましたね。それでは、このひし形を変形させます。テレビを見てくださいね。（アプリGeoGebraを用いて、ひし形をたこ形に変形させる）

わあ！　ひし形が動いて、凧みたいな形になった。

この図形をたこ形と言います。このたこ形の面積もひし形の公式を使って求めることができますか。１人１台端末に先生が用意したたこ形があります。図形に書き込んだり、ひし形と比べたりしながら、公式が使えるかどうかを調べて、その理由をノートに書きましょう。

公式の分からない図形でも、既習の形に変形することで面積を求めることができる。ひし形やたこ形の面積を求めるときには対角線に着目すると便利である。

評価問題

ひし形の対角線を移動してできたたこ形の面積は、ひし形の公式を使って求積することができるかな。

子供に期待する解答の具体例

たこ形の面積はひし形の公式を使って求めることができます。なぜなら、分割してできた２つの三角形の底辺の長さは対角線の長さと同じで、高さは対角線の長さの半分と同じだからです。
たこ形の面積はひし形の公式を使って求めることができます。なぜなら、変形してできた長方形の縦と横の長さは対角線の長さと同じだからです。
たこ形もひし形も対角線の長さは変わらずに直交しているから、できる図形の面積は変わらない。

※たこ形の面積を求めるときにひし形の公式が使えることを説明していく過程で、構成要素同士が直交しているという関係に気付かせましょう。そして、その構成要素間の関係が他の図形にも当てはまることを統合的に理解できるようにします。