小5算数「わり算と分数」指導アイデア《分数倍の意味》
執筆/横浜市立さつきが丘小学校教諭・岡田かおり
監修/文部科学省教科調査官・笠井健一
島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 分数の意味に着目し、整数の除法の結果を分数で表す方法を考える。
▼
第2時 商分数の適用問題
▼
第3時(本時)整数倍や小数倍の分数倍の意味を基に、分数倍の意味について考える。
▼
第4時 分数の意味に着目し、分数を小数や整数で表す方法を考える。
▼
第5時 小数や整数の意味に着目し、小数や整数を分数で表す方法を考える。
本時のねらい
除法の結果を表す分数を倍の場面でも適用できるか、整数倍や小数倍の学習を基に説明している。
評価規準
・分数倍の意味について、除法の結果を表す分数を倍の場面でも適用できる考えを広げ、説明している。
本時の展開
前回までの学習を確認します。どんな学習をしていましたか。
わり算の商は分数でも表せることが分かりました。
今までわり算で求めてきたものは分数でも表せるということですか。では、この問題はどうですか。

3mの赤いテープと2mの白いテープがあります。白は赤の何倍ですか。
今日は、倍を求めるのか。
倍を求めるときは、(比べられる量)÷(基にする量)だったね。基にするのは赤いテープだから2÷3だね。
ということは、[MATH]\(\frac{2}{3}\)[/MATH]倍ということかな。
[MATH]\(\frac{2}{3}\)[/MATH]倍とはどういうことだろう。
2÷3を計算すると、0.666……になるよ。
[MATH]\(\frac{2}{3}\)[/MATH]も0.666……も、どちらも1の半分よりも少し大きいから……。
初めて聞いたけど、[MATH]\(\frac{2}{3}\)[/MATH]倍でも合っていそうな気がする。
わり算の商は分数で表せたから、分数で表してもいいと思う。
では、今日は倍を分数でも表せるのか確かめてみましょう。

倍を分数でも表せるのかを考えよう。
見通し
式にすると2÷3だから、[MATH]\(\frac{2}{3}\)[/MATH]倍ということかな。(方法の見通し)
数直線を使えば、確かめられそう。(方法の見通し)
整数や小数の倍と同じように分数でも倍を表せそうだ。(結果の見通し)
自力解決の様子
A つまずいている子
わり算の商は分数に表せることは分かるが、白が赤の[MATH]\(\frac{2}{3}\)[/MATH]倍であることがどういうことか説明することが難しい。
B 素朴に解いている子
赤の3mを1として見ると、2mは[MATH]\(\frac{2}{3}\)[/MATH]に当たることを図を用いて説明している。
C ねらい通り解いている子
基準量を変えても同じように言えるのか、他の数でも考え、説明している。
学び合いの計画
本学習では、除法の商は分数(A÷B=[MATH]\(\frac{A}{B}\)[/MATH])を用いて表せるという考えを使って、倍も分数を用いて表すことができるのかを考えます。今まで学習した整数や小数での倍の表し方と同じように、「一方を1と見たときに、もう一方がどれだけに当たるか」という考え方を分数で表してもよいかを考察することを通して、倍の意味を統合させていきます。
また、数の量的概念をイメージしやすいように、数直線や図を用いることによって大きさの関係を視覚的に捉えやすくします。今まで、整数や小数で表せなかった数を分数なら表すことができることのよさを実感させることも大切です。小数倍で関係を捉えるよさや、分数倍で関係を捉えるよさについても考察し、自分の言葉で説明できるような場面を意図的に設定する必要もあると考えます。
また、一方からの見方だけでなく、基準量を変えても同じことが言えるのか、他の数でも表せるのか考えていきます。一方だけの見方だけでなく他方からも見ることのよさを実感させていきたいです。
ノート例
A つまずいている子
B 素朴に解いている子

全体発表とそれぞれの考えの関連付け
※C1、C2のそれぞれが発表をする。
C1
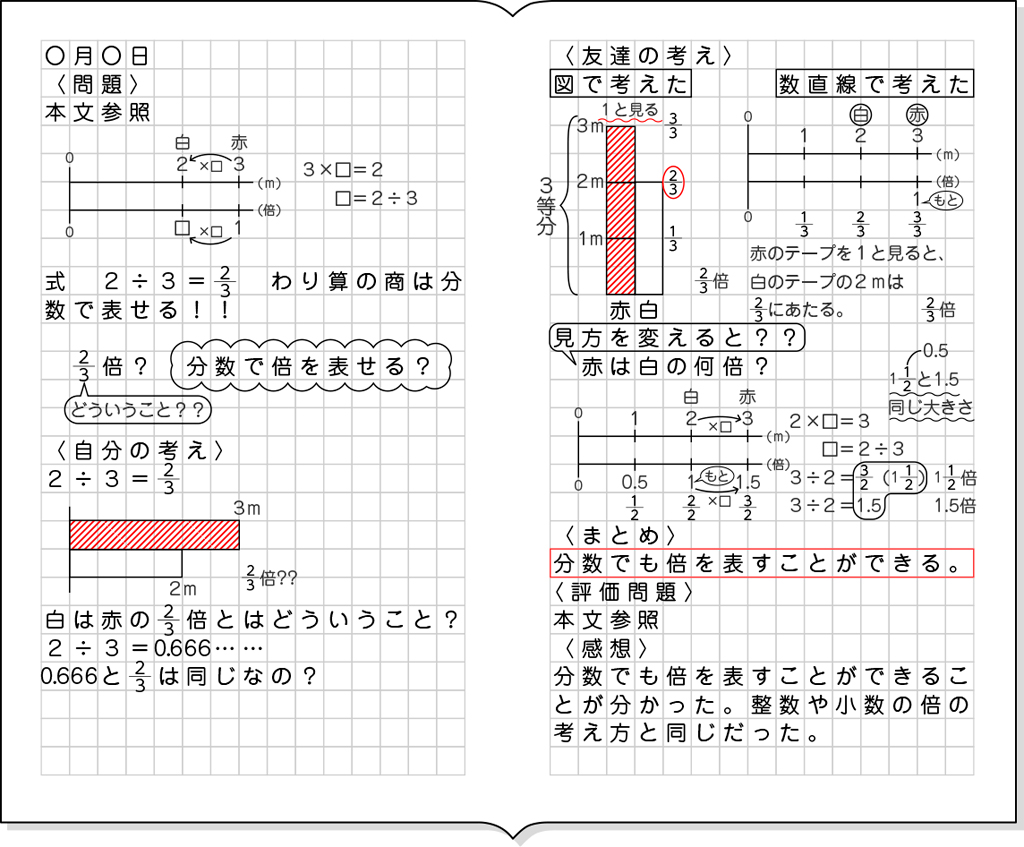
図で考えました。赤のテープを1と見たとき、1mが[MATH]\(\frac{1}{3}\)[/MATH]、2mが[MATH]\(\frac{2}{3}\)[/MATH]、3mが[MATH]\(\frac{3}{3}\)[/MATH]になるので、白の2mは[MATH]\(\frac{2}{3}\)[/MATH]倍です。
C2
数直線で考えました。赤のテープの3mを1と見ると、白のテープは3等分したうちの2つ分だから白は[MATH]\(\frac{2}{3}\)[/MATH]倍です。
2人の共通しているところは何でしょう。
イラスト/横井智美

