小2算数「大きい数のたし算とひき算」指導アイデア《3位数-2位数の筆算》

執筆/新潟大学附属新潟小学校教諭・石塚正人
監修/文部科学省教科調査官・笠井健一、新潟市立新津第一小学校校長・間嶋哲

目次
単元の展開
第1時 2位数+2位数=3位数(百の位への繰り上がりあり)の筆算の仕方を理解し、その計算ができる。
▼
第2時 2位数+2位数=3位数(十、百の位への繰り上がりあり)や2位数+1・2位数=3位数(百の位への波及的繰り上がりあり)の筆算の仕方を、数の見方や既習の加法筆算の仕方を基に考え、説明することができる。
▼
第3時 学習内容を適用して、問題を解決する。
▼
第4時(本時)3位数-2位数(百の位からの繰り下がりあり)の筆算の仕方を理解し、その計算ができる。
▼
第5時 3位数-2位数(十、百の位からの繰り下がりあり)の筆算の仕方を基に考え、説明することができる。
▼
第6時・第7時 3位数-1・2位数(十、百の位からの波及的繰り下がりあり)の筆算の仕方を理解し、その計算ができる。
▼
第8時 3位数+1・2位数(百の位への繰り上がりなし)や3位数-1・2位数(百の位からの繰り下がりなし)の筆算の仕方を理解し、その計算ができる。
▼
第9時 3位数+1・2位数(百の位への繰り上がりあり)や3位数-1・2位数(百の位からの繰り下がりあり)の筆算の仕方を理解し、その計算ができる。
▼
第10時 学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り、価値付ける。
本時のねらい
3位数-2位数(百の位からの繰り下がりあり)の筆算の仕方を考える。
評価規準
3位数-2位数(百の位からの繰り下がりあり)の筆算の仕方を考え、計算することができる。(思考力・判断力・表現力等)
本時の展開
色紙をたくさん持っていました。いっぱい使いました。残りは何枚でしょう。(大型提示装置に色紙のイラストを提示する)

「たくさん」だと、もともと何枚持っていたか分かりません。
「いっぱい」も「たくさん」と同じで、何枚使ったか分かりません。
このままだと、残りが何枚か求めることができません。
なるほど。持っていた折り紙は124枚です。使った枚数は63枚です。

色紙を124まいもっていました。63まい使いました。のこりは何まいですか。
※大型提示装置に色紙のイラストを提示しつつ、子供のタブレット端末に問題を配信する。
残りを求める式は、124-63だね。
数が大きくて、計算するのが大変だな。
たし算のときみたいに、筆算を使えばいいと思います。
ひき算でも、筆算を使って計算できそうなのですね。それでは、筆算を使って計算してみましょう。
1人1台端末活用アイデア①
本時のように、問題提示の場面で1人1台端末を活用しましょう。文章だけよりも日常生活に近付けた状態で問題場面を提示したり、数学的な見方を働かせるため手立てしたりすることができます。
まず、枚数が分からない状態で色紙を提示します。日常生活では枚数が分からない状態が普通ですし、子供から「枚数が知りたい」という言葉を引き出すためです。次に、持っていた色紙、使った色紙の枚数を提示します。このとき、持っていた色紙は位ごとに分けたイラストにします。100枚の束、10枚の束、1枚のばらを視覚的に捉えさせ、位を意識させるためです。自力解決や全体発表において、筆算の手続きを図や数の操作と関連付けて理解するためのヒントになるでしょう。

大きい数のひき算を筆算で計算するには、どうやればよいだろうか。
見通し
これまでみたいに、筆算は位を揃えて書けばいいかな。
たし算と同じように、位ごとに計算すればいいかな。

自力解決の様子
A つまずいている子
繰り下がりの処理が分からず、十の位を6-2と計算している。
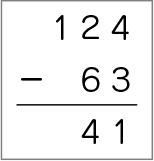
B 素朴に解いている子
124を100と24、63を60と3に分けて計算した後、筆算の答えを書いている。
124:100と24
63:60と3
100-60=40
24-3=21
40+21=61
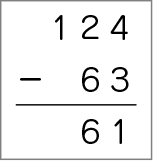
C ねらい通り解いている子
百の位から繰り下げて筆算している。
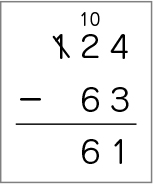
学び合いの計画
見通しの場面で、これまでのように「筆算は位を揃えて書く」ことや「位ごとに計算する」ことなど、既習事項を想起した子供の発言やつぶやきを価値付けることが大切です。こういった積み重ねにより、子供は、これまでに学んだことをふり返ったり、解決に生かしたりするようになるでしょう。
全体発表の場面では、子供が考えを発表する前に、「困ったことはありましたか」や「困ったところはどこですか」というように、解決に向けて困難だったことを問いましょう。本時では、十の位の計算ができないことが子供から出てくるでしょう。教師はこの困り感に寄り添い、このままでは計算できないことを全体で共有します。こうすることで、つまずいている子供には、「自分だけができないわけではない」という安心感を与えることができます。さらに、ねらい通りに解いている子供には、何を意識して考えを発表すればよいか、発表のポイントが明確になるでしょう。
その後、ねらい通りに解けている子供が筆算の仕方を発表するのではなく、紙の枚数を半具体物に置き換え、それらを操作しながら計算の仕方を全体で共有します。半具体物の操作と筆算における繰り下がりの処理とを関連付けるためです。これにより、子供は筆算における繰り下がりの処理(百の位の「1」を消すこと、十の位に「10」と書くこと)を理解することができるでしょう。
1人1台端末活用アイデア②
ブロックや数え棒など、半具体物はいくつかありますが、本実践では、半具体物としておはじきを使います。筆算の手続きと半具体物の操作とを関連付けるためには、数の相対的な大きさを表すのに適しているおはじきを使うことが効果的だと考えるからです。
まず、位ごとにおはじきの色を指定します。本実践では、百の位は赤、十の位は青、一の位は黄色としました。子供にとっては、100円玉、10円玉、1円玉硬貨と同じように考えることができます。次に、おはじきを操作しながら計算の仕方を考えます。おはじきを取ることが、ひき算という計算と同じことになります。このとき、操作の結果をタブレット端末で写真に撮るとよいでしょう。操作の過程を残すことができます。また、1人1人のタブレット端末に、おはじきのイラストをシートにして配信することも効果的です。おはじきのイラストを消すことがひき算と同じであること、百の位のおはじきを消して、十の位のおはじき10個増やすことが繰り下がりの処理と同じであることを、視覚的に理解することができます。
ノート例
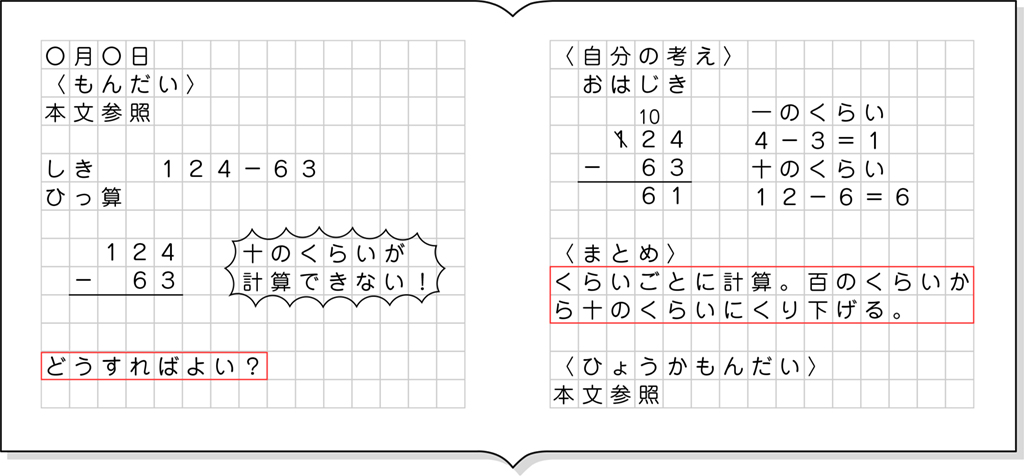
全体発表とそれぞれの考えの関連付け
困ったことはありましたか。困ったところはどこですか。
イラスト/横井智美、やひろきよみ

