小６算数「角柱と円柱の体積」指導アイデア《直方体を組み合わせた複合図形を角柱と見る体積の求め方》
執筆／富山大学教育学部附属小学校教諭・羽柴直子
監修／文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一
目次
単元の展開
第１時 第５学年で学習した体積の学習をふり返り、体積の意味を確認する。
▼
第２時 図形の構成要素に着目し、直方体の体積を求める公式を捉え直し、四角柱の体積の求め方を考える｡
▼ 《四角柱の体積の求め方》
第３時 図形の構成要素に着目し、三角柱の体積の求め方を考える。
▼
第４時 図形の構成要素に着目し、円柱の体積の求め方を考える。
▼ 《円柱の体積の求め方》
第５時（本時）図形の特徴に着目し、直方体を組み合わせた複合図形を角柱と見て、体積の求め方を考える。
▼
第６時 学習内容の習熟・定着を図る。
本時のねらい
直方体を組み合わせた複合図形の体積の求め方を、図形の特徴に着目し、図形の面積の学習と関連付けたり角柱と見たりして、図や式を用いて考え説明する。
評価規準
直方体を組み合わせた複合図形の体積について、図形の特徴や図形を構成する要素などに着目し、どの面を底面と見るとよいかを考え、既習の公式が適用できることに気付き、図形の面積の学習と関連付けたりして図や式を用いて考え、説明している。（思考･判断･表現）
本時の展開
図のような立体の体積を求めましょう。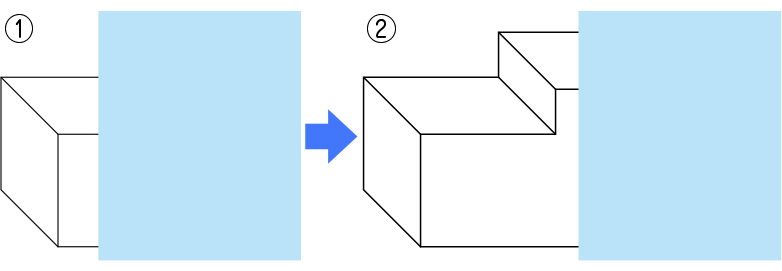
今日、体積を求める立体はこれです。
※①立体を紙で隠した状態から、少しずつ見せていく。
直方体だ！
簡単です。角柱の体積の公式「底面積×高さ」で求めることができます。
※②さらに紙をずらし、立体を提示する。
あれ。直方体ではないよ。階段みたいになっている。
これでは、「底面積×高さ」の角柱の公式を使って体積を求めることはできないよ。
この立体では、どうして角柱の公式が使えないのですか。
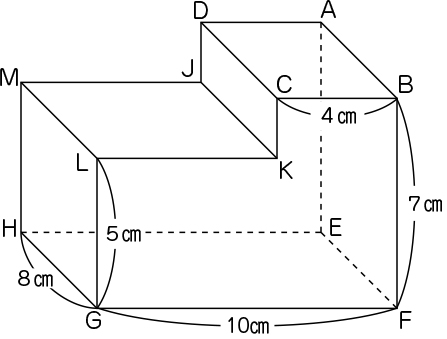
底面積は８×10で80㎠と求められるけれど、高さが５cmと７cmの２種類あって、どちらを使えばいいか分からないからです。
本当に底面積は80㎠と言えるのかなあ。角柱の底面は、上下に向かい合った合同な面だよ。面ＥＦＧＨと合同な面はないから、底面とは言えないのではないかなあ。
確かにそうだね。そしたら、５年生で学習した分割して求める方法で求めるしかないのかな。
う〜ん。でも、｢底面積×高さ」で求める方法があるかもしれない。考えてみようよ。
「底面積×高さ」の公式を使って、体積を求める方法を考えよう。
見通し
公式「底面積×高さ」を使うために、どの面を底面と見ればいいか考えよう。（方法の見通し）
５年生で学習した分割して求める方法を使えば、立体の体積を求めることができる。（結果の大きさの見通しなど）
自力解決の様子
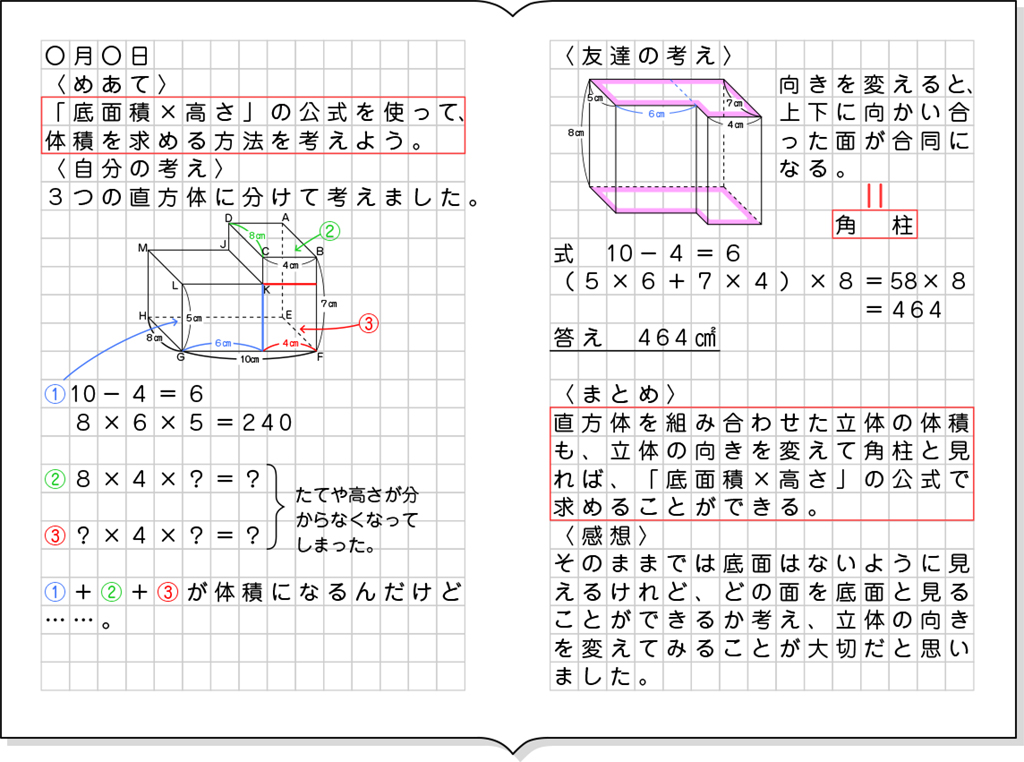
A つまずいている子
・５年生で学習した分割して求める方法で体積を求めている（３つの直方体に分けて考えている）。
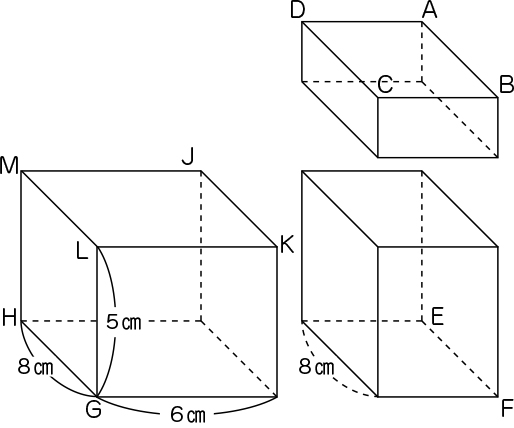
細かく分けたため、必要とする長さがよく分からなくなっている。
８×６×５＝240
８×？×？
８×４×？
答え ？㎤
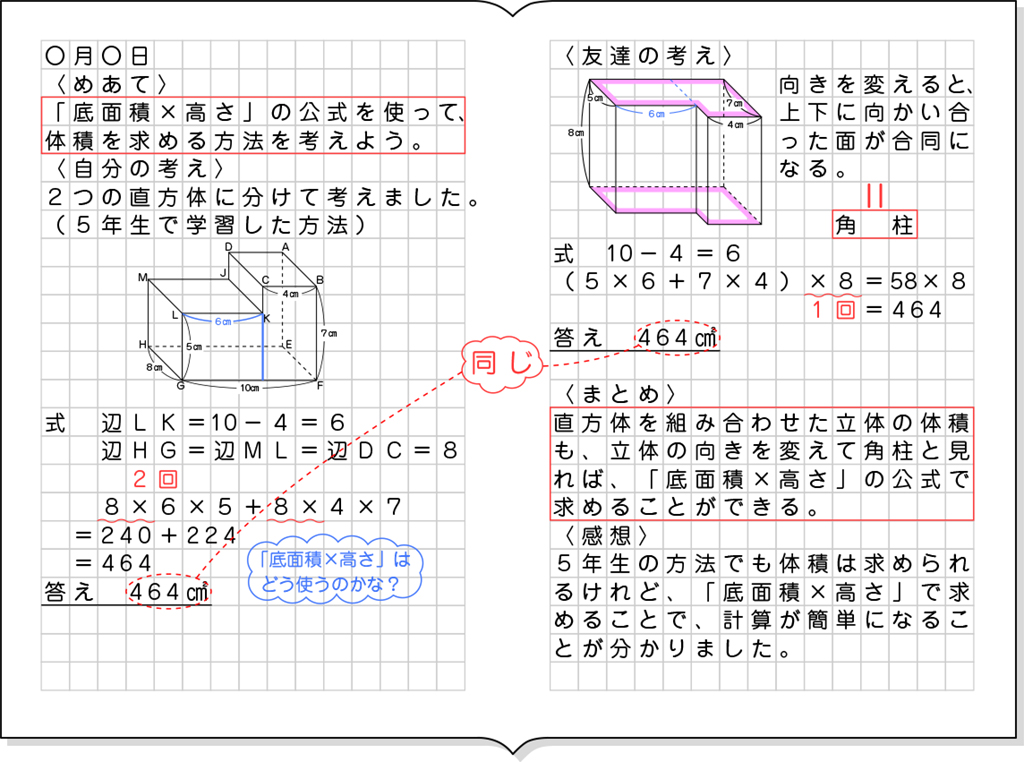
Ｂ 素朴に解いている子
・５年生で学習した分割して求める方法で体積を求めている（縦で切り、２つの直方体に分けて考えている）。
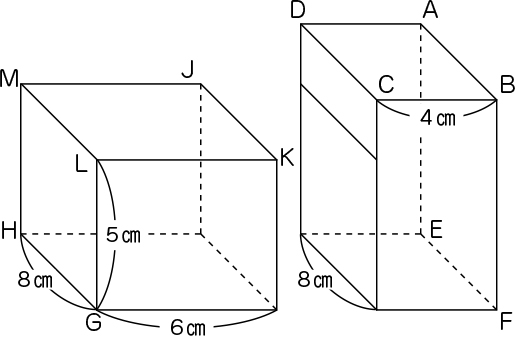
辺ＬＫ＝10－４＝６cm
辺ＨＧ＝辺ＭＬ＝辺ＤＣ＝８cm
８×６×５＋８×４×７＝240＋224＝464
答え 464㎤
Ｃ ねらい通り解いている子
・立体の向きを変えて、面ＬＧＦＢＣＫを底面と見て考えている。
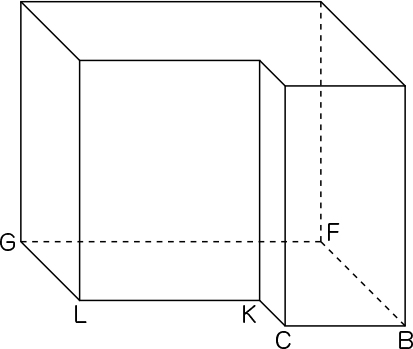
辺ＬＫ＝10－４＝６cm
（５×６＋７×４）×８＝58×８＝464
答え 464㎤
さらに、５年生で学習した分割して求める方法で体積を求めている。
辺ＬＫ＝10－４＝６cm 辺ＨＧ＝辺ＭＬ＝辺ＤＣ＝８cm
８×６×５＋８×４×７＝240＋224＝464
答え 464㎤
「底面積×高さ」で求めた体積を、５年生で学習した分割して求める方法で求めた体積と比べ、等しくなっていることを確かめている。直方体を組み合わせた複合図形の体積も、角柱と見れば、「底面積×高さ」で求められることに気付いている。
学び合いの計画
本時は、直方体を組み合わせた複合図形の体積を求める場面です。複合図形の体積は、第５学年において、既習の直方体に分割などし、「縦×横×高さ」で求める学習を行っています。そのため、本時の問題に対しても、５年生で学習した分割して求める方法で解決したらよいと考える子供もいるでしょう。しかし、本時では、複合図形が、既習の角柱の体積を求める公式「底面積×高さ」を適用することができることに気付き、図や式を用いて考え説明することを大切にします。さらに、「底面積×高さ」で考えるよさを実感できるようにしていきます。
しかし、子供たちにとって、紙にかかれた図を見て頭のなかだけでイメージし、立体の向きを変えたり底面を見付けたりすることは容易ではありません。そこで、自力解決や全体発表において、具体物を操作したり見せながら説明したりする手立てが大切になってきます。とくに体積を求めるために必要な辺の長さがどれかを捉えにくい子に対しては、問題の立体の模型を手渡して、例えば、８cmの長さの辺ＨＧと同じ長さの辺を調べさせて、辺ＨＧ、辺ＥＦ、辺ＡＢ、辺ＤＣ、辺ＪＫ、辺ＭＬに同じ色をつけてみるように促すなど、子供の理解と納得を深めるためのていねいな指導が大切です。
また、５年生で学習した分割して求める方法で求めた式と、角柱の体積の公式で求めた式を比較する場を設定します。そうすることで、より簡潔に求められることが明確になり、「底面積×高さ」で考えるよさの実感につながります。
ノート例
Ａ つまずいている子
Ｂ 素朴に解いている子
全体発表とそれぞれの考えの関連付け
この立体の体積を求めることはできましたか。
できました。464㎤です。
私も464㎤になりました。でも、「底面積×高さ」の公式を使う方法は思い付きませんでした。
僕もです。「底面積×高さ」は角柱の体積を求める公式です。今日の立体は角柱ではないと思うから、使えないと思います。
そうそう。角柱は、上下に向かい合った合同な面がある立体図形だけど、この立体は上下に向かい合った面は合同ではないよね。
では、464㎤は、どのようにして求めたのですか。
５年生で学習した分割して求める方法で体積を求めました。ここで縦で切り、２つの直方体に分けました。
辺ＬＫの長さは、10－４で６cmになります。辺ＨＧと辺ＭＬと辺ＤＣの長さはすべて等しく、８cmです。だから、式は、８×６×５＋８×４×７＝240＋224＝464。答えは、464㎤になります。
辺ＨＧが８cmというのは、問題に書かれていますね。辺ＤＣは、本当に８cmですか。
直方体の性質から、辺ＤＣが８cmだと説明することができます。
どんな性質なのか、くわしく話してください。
直方体には、同じ長さの辺が４つずつ３組あるという性質です。直方体のなかの平行な４つの辺は同じ長さです。辺ＨＧと辺ＥＦは平行だから、辺ＥＦの長さは８cmです。そして、辺ＥＦと辺ＤＣは平行だから、辺DＣの長さは８cmです。
筋道立てて分かりやすい説明でしたね。今の説明で、みなさんは納得できていますか。
※多くの子供が納得しているなかで、不安そうな顔を見せている子に問題の立体図形の模型を渡す。
○○さん、みんなが安心して学習を進めていけるように、辺ＨＧと辺ＤＣの長さを実際に測ってみてください。
〈○○さん〉（具体物を実際に測る）８cmになりました。辺ＨＧも辺ＤＣも８cmでした。
○○さんのおかげで、辺ＤＣが８Cmだということに自信をもって、考えていけますね。
僕は、直方体３つに分けて、辺の長さがよく分からなくなってしまい困っていました。でも、今の話を聞いていて、少し分かってきました。念のために、実際に長さを測ってみようと思います。
考えを進めていけそうでよかったですね。
でも、本当は、２つの直方体に分けて考えたほうが簡単にできそうだと思い始めています。
８×６×５＋８×４×７の８×６と８×４は底面積、５と７は高さと見ることができるから、「底面積×高さ」の公式を使っていると言えるのではないかな。
なるほど。２つの直方体に分けてからだったら、公式に当てはめることができるね。
「底面積×高さ」の公式を使って体積を求める方法は、これでいいですか。
私は、直方体に分けなくても「底面積×高さ」の公式を使うことができました。
えっ。どういうこと。
この立体の向きを変えるといいんだよ。
みんなが分かるように、立体を操作して見せてください。
これを、こんなふうに前に倒します。そうすると、面ＬＧＦＢＣＫが底面になります。
長方形でも正方形でもないのに、底面と言えるのかな。
底面は、上下に向かい合った合同な面です。面ＬＧＦＢＣＫと面ＭＨＥＡＤＪは合同になっているから、底面と言えるよ。
確かに。立体の向きを変えただけで、底面ができるんだ。
辺ＬＫは、10－４で６cm。底面ＬＧＦＢＣＫの面積は､（５×６＋７×４）で求められるから、｢底面積×高さ」の公式に当てはめると､（５×６＋７×４）×８＝58×８＝464となり、答えは、464㎤になります。
みなさん、納得できましたか。
｢底面積×高さ」で求めた体積も、５年生で学習した分割して求める方法で求めた体積も、両方464㎤になっているよ。
ということは、立体の向きを変えて考えてもよいということになるね。
直方体を組み合わせた複合図形の体積も、向きを変えて角柱と見れば、「底面積×高さ」で求められるんだね。
僕は今まで、角柱というのは立方体や直方体、五角柱、六角柱……のような立体のことだけだと思っていたよ。
私もです。角柱というのは底面の形が正多角形だと思い込んでいました。
でも、今回の勉強を通して、底面の形と合同な面が積み上がっている立体図形は角柱と見てもよいということが分かりました。
だから、今日の問題の立体だけではなくて、こんな（ジェスチャーで表そうとしている）立体でも……。
黒板にかいてみてください。
はい。例えば、こんな図形も角柱と見てもよいと思います。
そうか。立体の向きを変えれば、この面が底面となる角柱として見ることができるね。
こんな図形も角柱と見ていいよね。この面が底面になるよね。
５年生で学習した分割して求める方法の式と「底面積×高さ」で求めた式を見て気が付いたんだけど……。
何を気が付いたのですか。みんなも比較してみましょう。
８×６×５＋８×４×７＝240＋224
＝464
（５×６＋７×４）×８＝58×８
＝464
５年生で学習した分割して求める方法のほうは、８が２回出てくるね。でも、「底面積×高さ」のほうは、８が１回しか出てきません。
直方体に分けて考えると、分けた数の分だけ高さを掛けなければいけないのだね。
でも、立体の向きを変えて角柱と見れば、高さは１回掛けるだけでよくなるんだね。
ずいぶん計算が簡単になるね。
どの面を底面と見ることができるか考えることが大切だね。
学習のまとめ
立体の向きを変えて、面ＬＧＦＢＣＫを底面と見て考える。
式 辺ＬＫ＝10－４＝６cm
（５×６＋７×４）×８＝58×８＝464
答え 464㎤
このような立体の体積も、角柱と見れば、「底面積×高さ」の公式で求めることができる。
- どの面を底面と見ることができるか考えることが大切！
- ５年生で学習した分割する方法でも求められる。でも、「底面積×高さ」で求めたほうが、高さを１回掛けるだけだから計算が簡単！
評価問題
下の図の立体の体積を求めましょう。
子供に期待する解答の具体例
立体の向きを変えて、面ＢＦＧＬＫＣが底面の角柱と見て考えている。
辺ＫＬ＝９－４＝５cm
（８×４＋４×５）×７＝52×７＝364
答え 364㎤
本時の評価規準を達成した子供の具体の姿
直方体を組み合わせた複合図形の体積について、どの面を底面と見るとよいかを考え、角柱の公式を適用して考えている。
感想例
- 直方体を組み合わせた立体の体積も、「底面積×高さ」の公式で求められることが分かりました。
- そのままでは底面はないように見えるけれど、どの面を底面と見ることができるかなあと考え、立体の向きを変えてみることが大切だと考えました。
- ５年生で学習した分割して求める方法でも体積を求められるけれど、「底面積×高さ」で求めることで、計算が簡単になることが分かりました。
- 直方体を組み合わせた立体の体積を求めるときは、立体の向きを変えてみて、底面を見付けたいと思います。
- 角柱というのは底面の形が正多角形だと思い込んでいましたが、底面の形と合同な面が積み上がっている立体図形は角柱と見てもよいのだなと思いました。
- ふり返ってみると、四角形は凸の形のものだけを考えてきたけれど、凹の四角形も考えてみるとよいかも知れないなと思いました。
板書例とワークシート
イラスト／横井智美
