6学年の内容だけを見て指導すると、点の指導になる【「系統」を見通し、学年ごとに押さえる! つまずきなしの「分数」指導法 #11】

前回は、分数を小数に直したり、小数を分数に直したりする授業について新潟市立上所小学校の志田倫明先生に説明していただきました。今回は、6学年の学習のポイントとなる分数の乗法、除法について解説をしていただきます。
目次
かけ算は比例関係を前提とした倍の考え方に拡張

前回、分数としての学習は5学年まででほぼ完結しているため、6学年では分数の意味を活用して問題解決をすることが主な学習になるということに触れました。この6学年の学習で中心となるのは、分数の乗法と除法になります。ですから、この内容について乗法と除法に分け、今回はまず乗法(かけ算)から説明をしていきたいと思います。
以前、分数のたし算の学習で、2学年から何を学んできたかを捉え直していく授業について説明をしましたが、それと同様に、かけ算の学習でも意味を捉え直していくことが大切です。ちなみにたし算、ひき算については、同種同単位のものであれば計算ができるということが原理原則としてありました(連載第8回参照)。しかし、かけ算の場合は少々複雑で、5学年での×小数の学習のときに、すでに大きな意味の拡張を迫られていたのです。
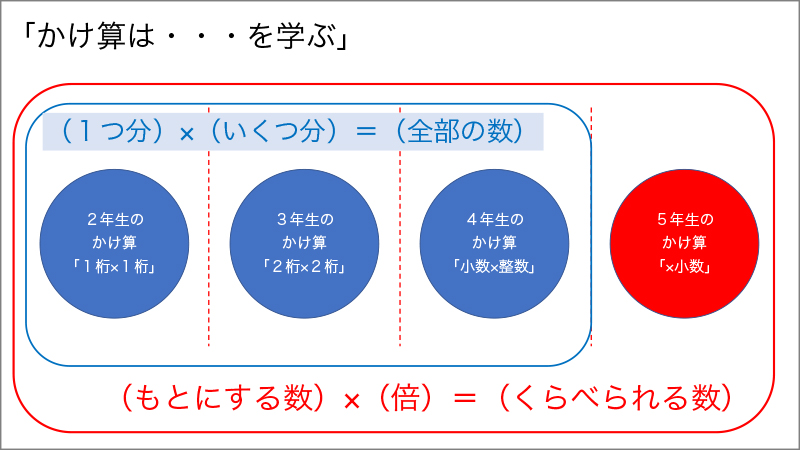
5学年以前のかけ算では、子供たちは1つ分×いくつ分=全部の数、という意味でかけ算を学んできています。例えば、袋の中にあめ玉が3つ入っていて、それが4袋あると、全部のあめ玉の数は3×4=12 で、12個という計算になるわけです。ところが、×小数になった途端に、その意味では説明ができなくなります。例えば、1mが80円の紙テープがあり、それを2.3m買ったらいくらかというときに、「80×2.3としていいのかな?」というところで、子供はつまずくのです。
実は4学年までのかけ算は、たし算に直して意味を説明することができます。いわゆる同数累加の考え方で、先のあめ玉の例なら3×4=3+3+3+3=12となるわけです。ところが紙テープの例では、80×2.3=80+80+(80ではないもの)となります。このように同じものをたしているわけではないのに、かけ算と認めてよいのかということで、説明が付かなくなり、真剣に意味を考えることで、かえって混乱してしまう子供もいるのです。
では、それをどう乗り越えるかというと、かけ算は比例関係を前提とした倍の考え方で意味付けられると拡張するわけです。つまり、「1mあたり80円としたときに、2.3mは基の1mを2.3倍しているから、値段も2.3倍になるであろう」と比例を仮定することで、かけ算が成立すると考えるのです。そういう意味で見返してみると、あめ玉の例も「袋が4倍になっているから、中身のあめ玉だって4倍になる」という倍の考え方と同じことをやっていた、と捉え直されるようになるわけです。つまり、×小数を学ぶことによって、それまで学習したかけ算(1つ分×いくつ分=全部の数)もすべて、2量の比例関係を前提とする倍の考え方の説明で包含できるというように、意味の拡張が図られるわけです(資料1参照)。
(資料1)