小5算数「割合」指導アイデア《比較量と割合から基準値を求める》
執筆/富山県射水市立大島小学校教諭・前田正秀
監修/文部科学省教科調査官・笠井健一
前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 シュートの入った回数とシュートした回数の関係に着目し、一番よく成功した人の比べ方を考える。
▼
第2時 シュートの入った回数とシュートした回数の関係に着目し、倍の意味を基にして、割合を用いた2つの数量の関係の比べ方について考える。
▼
第3時 2つの数量の関係に着目し、百分率や歩合での表し方を考える。
▼
第4時 基準量、比較量、割合の関係に着目し、基準量と割合から比較量を求める方法を考える。
▼
第5時(本時)基準量、比較量、割合の関係に着目し、比較量と割合から基準量を求める方法を考える。
▼
第6時 割合の適用問題に取り組む。
▼
第7時 和や差を含んだ割合の表現に着目し、基準量と割合から比較量を求める方法を考える。
▼
第8時 学習内容の生活への活用
▼
第9時 学習内容の習熟・定着
本時のねらい
基準量、比較量、割合の関係に着目し、比較量と割合から基準量を求める方法を図や式などを用いて考える。
評価規準
日常の事象における数量の関係のなかから、基準量、比較量、割合の関係に着目し、比較量と割合から基準量を求める方法について図や式などを用いて考え、説明している。(思考・判断・表現)
本時の展開

きょう、公園に来た子供は12人で、きのうの1.5倍の人数です。きのう、公園に来た子供は何人だったでしょう。
 関係を図で整理する
関係を図で整理する
割合の学習では、問題の提示の仕方がとても大切です。というのも、問題場面をしっかりとイメージし、基準量と比較量の関係を捉えることができれば、おおむね解決に向かうことができるからです。問題を提示する際には、子供と一緒に基準量と比較量の関係を図に表しながら、問題場面をていねいに確認していくのがよいと思います。
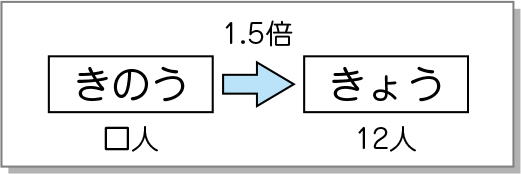
「きのう」と「きょう」の人数の問題ですね。まず、「きのう」と「きょう」を書きましょう。
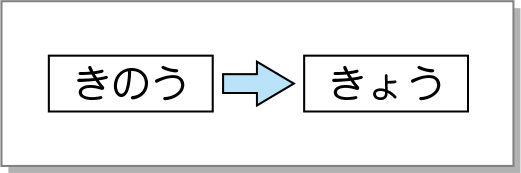
「きょう」は、「きのう」の何倍ですか。
1.5倍です。
「きのう」の「1.5倍」が「きょう」ですね。「きのう」と「きょう」の間の矢印に、「1.5倍」を書き入れましょう。
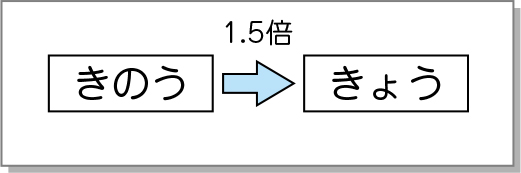
「きょう」来たのは、何人ですか。
12人です。
では、「きょう」に「12人」と書きましょう。
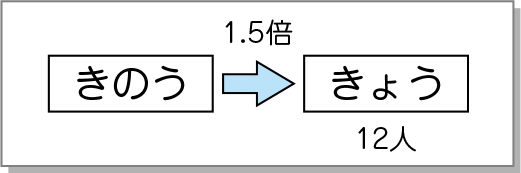
「きのう」来た人数は、まだ分かりませんから、「□人」としましょう。
 簡潔な文にして音読する
簡潔な文にして音読する
関係を図に表すことができたら、関係の図を声に出して読みます。
1回目は、言葉を使って、「きのうの1.5倍がきょう」とみんなで読みます。
2回目は、数を使って、「□人の1.5倍が12人」とみんなで読みます。
大きな声で口にすることで、子供たちは関係を捉えやすくなるのです。
それでは、関係の図を声に出して読みますよ。後に続いて言ってみましょう。きのうの1.5倍がきょう。
※子供たち全員が「きのうの1.5倍がきょう」と声を出す。
今度は数で言いますよ。□人の1.5倍が12人。
※子供たち全員が「□人の1.5倍が12人」と声を出す。
 前の時間との違いを明確にする
前の時間との違いを明確にする
子供たちが関係を捉えたところで、第4時までに解いてきた問題の図を見せ、今回の問題とこれまでの問題との違いを尋ねます。
さあ、どんな問題なのか、分かりましたね。では、今日の問題は、これまでの問題とどこが違いますか。
今日の問題は、基にする量を求める問題になっています。
そうですね。今日は基にする量の求め方を考えていきましょう。

基にする量の求め方を考えよう。
見通し
1.5倍が12人だから、答えは12人よりは少ない。(答えの見通し)
□の1.5倍が12になる。(方法の見通し)
12÷1.5で求めることができそう。(方法の見通し)
自力解決の様子
A つまずいている子
・どちらを基準量とするのかが、はっきりしていない。
・1.5倍の「倍」につられて、かけ算を考えている。
12×1.5=18
B 素朴に解いている子
・前時(第4時)に学習した「基準量×割合=比較量」を基にして考えている。
□×1.5=12
12÷1.5=8
C ねらい通り解いている子
・比較量と割合から基準量を求める方法について考えている。
12÷1.5=8
学び合いの計画
①求め方の比較
学び合いでは、まず、それぞれの求める方法を紹介し合います。
一番多い方法は、□を使って、□×1.5=12としてから、□=12÷1.5だと考える方法でしょう。この方法は、前時に学習した「基準量×割合=比較量」に当てはめ、分からない数を□を用いて表すことで、数量の関係が捉えやすくなるというよさがあります。
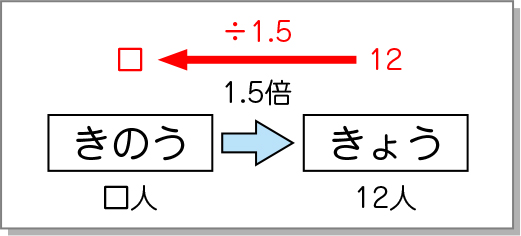
また、なかには、関係の図を逆から読んで、わり算の式を立てられる子供もいることでしょう。1.5倍して12になったのだから、12を1.5で割ればきのうの人数が分かるという考え方です。このやり方には、求める基準量を素早く捉えられるというよさがあります。
どちらも大切したい考えです。
②誤答との比較
上に記した2つのやり方は、いずれも正しいやり方です。しかし、正しいやり方ばかりを紹介していては、本当の理解にはつながりません。誤答を紹介し、それが間違っている理由を説明したり、正しい方法に修正したりすることで、さらに理解が深まるのです。
ここでは、12×1.5という誤答の例を紹介します。子供のなかには、こういう間違いをする子が多くいるからです。12を1.5倍しているのか、それとも1.5倍されたのが12なのかを、なかなか捉えられないのです。
誤答例を紹介して、間違っている理由を説明し合うことは、つまり、「基にする量が何なのか」について考えるということです。この考えが、割合の問題を解く際の基本になるのです。
ノート例
A つまずいている子

B 素朴に解いている子

全体発表とそれぞれの考えの関連付け
①求める方法の比較
□×1.5=12だから、12÷1.5をして8だと分かりました。
僕は□を使わず、すぐに12÷1.5という式にしました。
□を使った人と使わなかった人がいるんですね。□を使った人は、どうして使ったのですか。
イラスト/横井智美

