小3算数「円と球」指導アイデア（8/8時）《ボールがぴったり入った箱のまわりの長さ》
執筆／富山大学人間発達科学部附属小学校教諭・羽柴直子
編集委員／文部科学省教科調査官・笠井健一、前・富山県公立小学校校長・中川愼一
目次
本時のねらい（本時８／８時 円や球の性質について学習した後）
球の性質と円の性質を関連付けながら、球を囲む箱の周りの長さの求め方を円の直径の長さを基にして考える。
評価規準
問題を構成する要素に着目し、球をちょうど半分に切った場合の切り口が最大になるという性質を用いて、箱の周りの長さの求め方を考えている。（思考･判断･表現）
問題
同じ大きさのボールが８こ、ぴったり入ったはこがあります。
はこのたての長さは 20㎝でした。はこのまわりの長さは、どれだけでしょう。
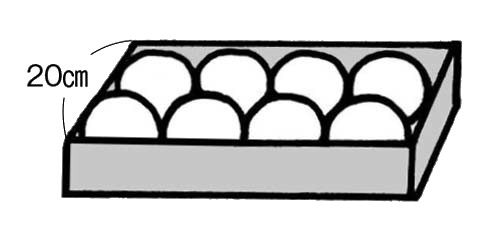
この箱の周りの長さを求めることはできそうですか。
箱を上から見た形は長方形だから、周りの長さは、縦の長さの２倍と横の長さの２倍を足したら求められると思います。
でも、縦の長さは20㎝だと分かっているけど、横の長さは分からないよ。
ボールは少しでこぼこしているけど、球の形と見ていけば求められそうだよ。球の切り口は円だということがヒントになるんじゃないかな。
学習のねらい
円をうまく使ってまわりの長さを考えよう。
見通し
・箱の縦の長さ 20cm から、ボール（球）の直径の長さが分かる。
・ボール（球）の直径の長さが分かれば、箱の横の長さが分かる。
自力解決の様子
Ａ つまずいている子
縦の長さしか分かっていないから、周りの長さは求められない。
Ｂ 素朴に解いている子
ボールが２個で 20㎝ なのだから、ボールが４個では 40㎝。
20 ＋ 40 ＋ 20 ＋ 40 ＝ 120
周りの長さは、120㎝。
Ｃ ねらい通り解いている子
「ボール、箱」を「円、長方形」とみなして考える。
長方形の縦や横の長さは円の直径の長さによって決まる。円が２つで 20㎝なので、１つの円の直径は 10㎝。
横の長さは、その４倍だから 40㎝。長方形の周りの長さは、直径の12倍だから 120㎝。
20 ÷ 2 ＝ 10 10 × 12 ＝ 120
学び合いの計画
ここでは、球を円と関連付けて捉える見方・考え方を大切にします。立体図形では考えにくくても、平面図形に置き換えると考えやすくなります。
また、縦の長さから直径の長さを導き出し、その直径の長さから周りの長さを導き出すという段階的な思考方法のよさを味わうことができるようにします。
問題場面は、同じ大きさの球が直方体の形をした箱にぴったり入っているという設定です。子供たちは、一見関係がまったくなさそうなボール（球） と直方体という２つの形にとまどうことでしょう。
そこで、円の学習と関連付けながら、球の定義や性質を調べた前時の学習が生きてきます。
ノート例
全体発表とそれぞれの考えの関連付け
箱の周りの長さを求めることができましたか。
箱の縦はボール２個で20㎝。箱の横はボール４個が並んでいて、縦の２倍だから、長さも２倍になるので 40㎝。周りの長さは 120㎝になりました。
私は、円を使えば周りの長さが求められると思ったけど、球の切り口はどこを切っても円になるから、どうしたらよいのか分からなくなりました。
球をちょうど半分に切ったときにできる円が一番大きくなるでしょ。箱に球がぴったり入るということは、長方形の中にその円がぴったり並んでいることと同じだから、直径の２つ分で 20㎝になるよ。
あっ、そうか！ ということは、この円の直径は 10㎝だ。箱の横の長さは直径が４つ分で 40㎝になるんだね。それで、周りの長さは、120㎝なんだね。
学習のまとめ
円が２個並ぶときは、直径の２倍の長さになる。
３個並べば３倍、４個並べば４倍…… 。
直径の長さを基にすれば、箱の大きさを求めることができる。
評価問題
上のように、直径が６㎝のボールがぴったり入ったはこがあります。
このはこのまわりの長さをもとめましょう。
解答
6 × 3 ＝ 18、6 ＋ 18 ＋ 6 ＋ 18 ＝ 48
1 ＋ 3 ＋ 1 ＋ 3 ＝ 8、6 × 8 ＝ 48
（答え）48㎝
本時の評価規準を達成した子供の具体の姿
直径の長さを基に、箱の周りの長さを考えている。
感想例
・箱とボールは全然関係ない形だと思っていたけど、箱を長方形、ボール（球）を円と考えたら、考えを進めるきっかけになりました。
・球（円）が箱（長方形）にぴったり入っているときは、直径のいくつ分で縦、横、周りの長さを求めることができることが分かりました。直径の長さに気付いたときは、すごくうれしかったです。
イラスト／小沢ヨマ、横井智美
『教育技術 小三小四』2021年8/9月号より
