小4算数「角の大きさ」指導アイデア《三角定規を使っていろいろな大きさの角をつくる》
執筆/富山県射水市立大島小学校教諭・前田正秀
監修/文部科学省教科調査官・笠井健一
前・富山県南砺市立福光東部小学校校長・中川愼一
単元の展開
第1時 角の大きさの意味を理解する。
▼
第2時 角の大きさの度の単位を知り、表し方を理解する。
▼
第3時 分度器を用いて角の大きさを測定する。
▼
第4時 180°より大きい角度の測定のしかたを考える。
▼
第5時(本時)三角定規を使っていろいろな大きさの角をつくる。
▼
第6時 分度器を使って角を作図する。
▼
第7時 分度器を使って三角形を作図する。
▼
第8時 たしかめ
本時のねらい(角の大きさの測定のしかたを学習した後)
三角定規を組み合わせてできる角の大きさについて調べ、角の大きさは足したり引いたりできるという見方を基に、柔軟に考えている。
評価規準
三角定規を組み合わせてできる角の大きさの求め方を考え、それを式で表して説明している。(思考・判断・表現)

三角定規を使うと、どんな角度がつくれますか。
三角定規には、2種類あります。どんな角度がありますか。
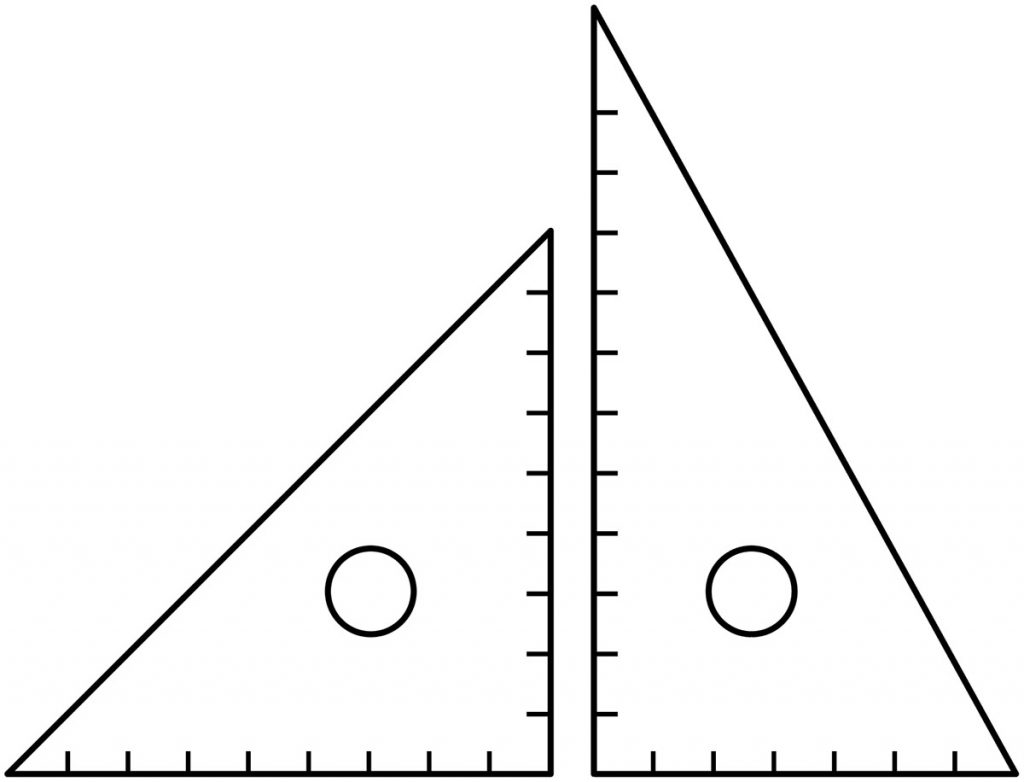
90°、60°、30°です。
もう1つの三角定規は、90°と45°と45°です。
そうですね。では、この三角定規を組み合わせると、どんな角度がつくれるでしょう。
組み合わせる……?
例えば、こんなふうに組み合わせると、ここは何度になっていますか。
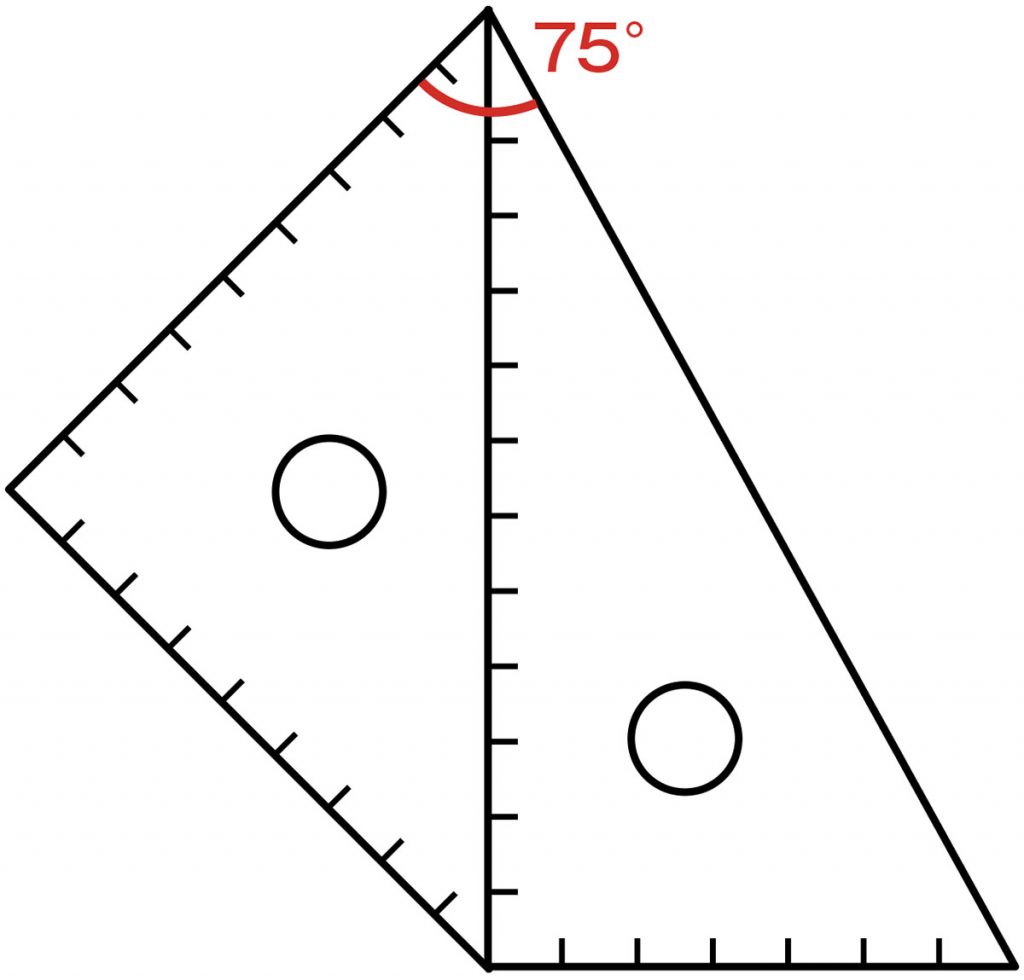
45°と30°だから、75°です。
式で表すと45+30=75です。
なるほど、そういうことか。だったら……。
いろいろな角度をつくることができそうですね。それでは、どんな角度をつくることができるのか、調べてみましょう。

三角定規を使ってつくれる角度について考えよう。
見通し
2つの三角定規の頂点と頂点をくっつけると、大きな角度をつくることができそうだ。(方法の見通し)
30°と45°をくっつけると、合わせて75°になるはずだ。(結果の見通し)
自力解決の様子
A つまずいている子
三角定規を操作はしているが、どことどこを合わせると、どんな角度になるのかという見通しをもたずに、やみくもに組み合わせている。
B 素朴に解いている子
2つの三角定規をくっつけて、頂点どうしを合わせて、75°(45°と30°)、105°(45°と60°)、120°(直角と30°)など、2つの角を合わせてできる角の大きさを調べている。
C ねらい通り解いている子
- 2つの三角定規を重ねて、15°(45°の上に30°)、15°(60°の上に45°)など、2つの角度の差も角度として認めている。
- 三角定規の辺(直線)を180°と見て、210°(180°と30°)、225°(180°と45°)などを調べている。
- 内側の角だけでなく外側の角についても認めて、285°(75°の外側の角の大きさ)などを調べている。
学び合いの計画①
机間指導の際には、「すごい。Aさんは、3つもできている」「おっ、Bさんは4つ」と数を実況中継しながら回るのも効果的です。周りの子が刺激を受け、自分もいっぱい見付けようとするからです。
たし算を使えば、75°、105°、120°、135°、150°、180°の5つまでは簡単につくることができます。なかにはもっと違った角度をつくることができないかと工夫を始める子が出てきます。
イラスト/横井智美


