小5算数「四角形と三角形の面積」指導アイデア
執筆／埼玉県公立小学校教諭・中山貴仁
編集委員／文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
（本時の位置 9／12時）
問題場面
ひし形の面積は、求め方を構成要素や性質に着目し既習の図形を基に公式を求めることができることを理解する。
評価規準
・ひし形の性質に着目し、面積の求め方を説明することができる。
・ひし形の求積公式がわかる。
問題
ひし形の面積はどのように求めるのだろう。
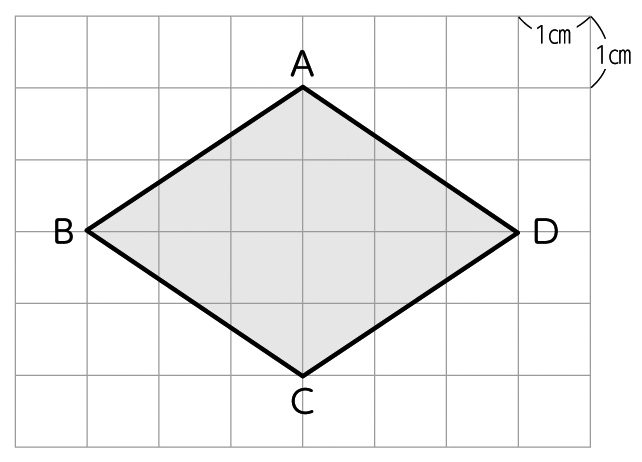
前時までに図形の面積をどのように求めてきましたか。
図形を切って場所を変えたり、もう一つ増やしたりすることで習ったことのある図形に変形して求めました。
台形では、2つつなげると平行四辺形になるという特徴を使って求めました。図形の特徴を用いて求めました。
では、ひし形の特徴を使って、面積を求めてみましょう。
ひし形には、どんな特徴がありますか。
対角線が垂直に交わります。
周りを囲む長方形の半分の大きさになっています。
辺BDで分けると1組の合同な二等辺三角形ができます。
2本の対角線で分けると4つの合同な直角三角形ができます。
本時の学習のねらい
ひし形の特ちょうを使って、面積の求め方の公式を作ろう。
対角線で分けると1組の合同な三角形ができるか……。
ひし形は周りを囲む長方形の半分の大きさになるから……。
今までも習った形に変形していたから……。
平行四辺形としてみることもできるから……。
自力解決の様子
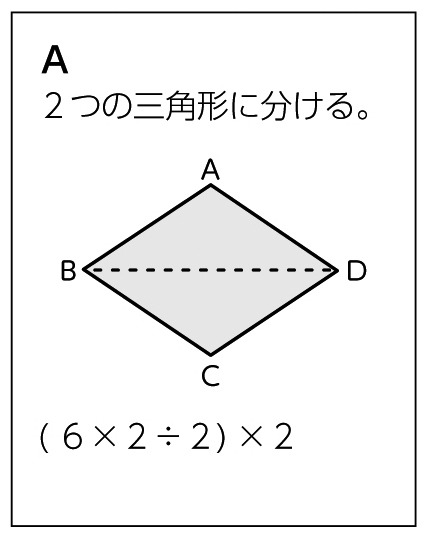
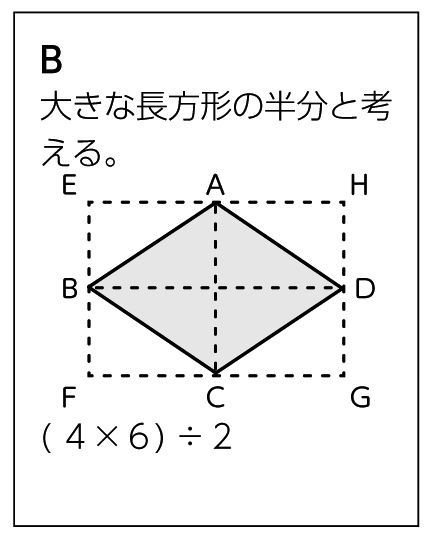
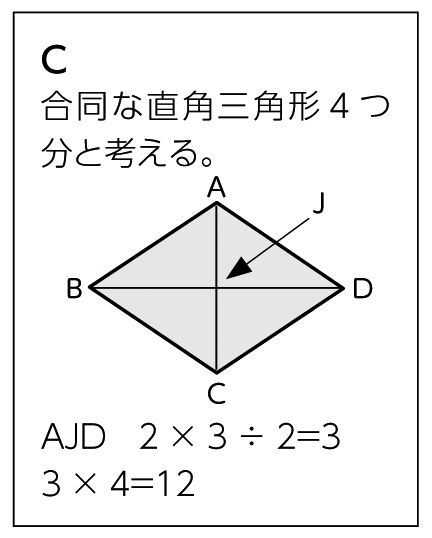
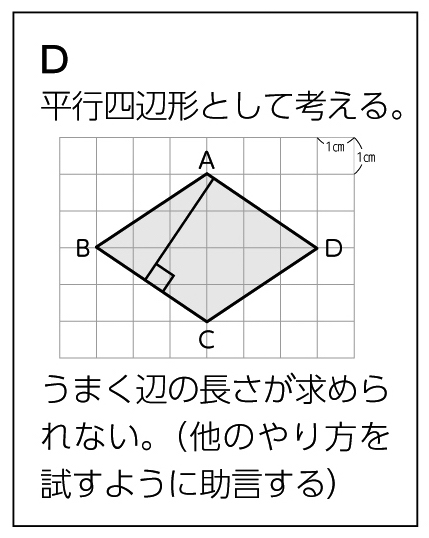
※方眼の数を数えている児童については、どのひし形の特ちょうを使えば今まで学習した図形の面積に結び付けられるか考えるように支援する。
学び合いの計画
イラスト／横井智美
『教育技術 小五小六』 2020年12月号より
