小６算数「比例と反比例」指導アイデア《比例の性質について考え、比例の関係は式で表すことができることを知る》
執筆／富山県高岡市立木津小学校教諭・屋鋪善祐
監修／東京都国立教育政策研究所教育課程調査官・加固希支男、富山大学附属小学校教諭・羽柴直子
目次
年間指導計画
・対称な図形
・文字を使った式
・場合の数
・分数×÷整数
・円の面積
・分数×分数
・分数÷分数
・角柱と円柱の体積
・資料の調べ方
・小数と分数の計算
・比と比の利用
・拡大図・縮図
・比例と反比例
・およその面積と体積
・算数のまとめ
単元の展開（各時の主な学習活動内容）
第１時 伴って変わる２つの数量の変わり方について考える。
第２時 紙・クリップの枚数と重さとの関係を調べ、説明する。
第３時 針金の長さと重さの２つの数量が伴って変わることを調べ、比例の意味について考える。
第４時（本時）比例の性質について考え、比例の関係は式で表すことができることを知る。
第５時 比例の性質を利用して、比例の関係を式で表す。
第６時 xとyの関係を式に表し、決まった数は何を表しているか考える。
第７時 比例の関係をグラフに表すことを考え、かき方と特徴を知る。
第８時 グラフを見て、比例しているかどうかを判断したり、数値を読んだりする。
第９・10時 比例の関係を表す式やグラフを用いて、問題解決の方法を考える。
第11時 反比例する２つの量の変わり方を調べ、反比例の特徴を考える。
第12時 反比例の性質を見付け、反比例を表す式やグラフについて考える。
第13時 反比例の性質を利用して、問題解決の方法を考える。
第14・15時 適用問題を解く。
本時のねらい
ｙがｘに比例するとき、ｙ＝決まった数×ｘと表せることを理解し、比例の関係を式に表すことができる。
評価規準
比例の関係のときに成り立つきまりに着目し、比例の式や「決まった数」の多様な意味について考察することができる。
本時の教材のポイント
比例の関係を式に表す授業では、「ｙ÷ｘはいつも決まった数になること」「ｙをｘの式で表すと、『ｙ＝決まった数×ｘ』になること」を押さえようと、教師主導な展開になりがちです。そこで大切にしたいのは、比例の関係を式に表すことのよさに気付く授業展開を意識することです。
本時の導入場面では、下のイラストのような直方体の水槽に水を入れていく動画を視聴します。２分後に水の深さが４cm、４分後に水の深さが８cmになることを確認し、表に書き込んでいきます。ここで一旦動画を止め、「６分後の水の深さは何cmになると思いますか？」「８分後の水の深さは何cmになると思いますか？」と問い、水を入れる時間と水槽の水の深さが比例の関係であることや、前時まで学習してきた変化のきまり（表を横の関係で捉える）を使って考えられることを確認します。その後、「では、13分後の水の深さは何cmになると思いますか？」と問います。もちろん変化のきまりで答えは求められますが、６分後や８分後のように整数倍で求められないことや、さらに数値が大きくなった場合のことに子供たちは気付くでしょう。子供たちのその気付きを大切にし、さらによい求め方がないか考えたいという思いを高めながら授業を展開していきます。そして、既習の立式の経験を想起し、ｘとｙの関係を表す式につなげていきます。
見通し場面では、これまで表を横で見ることが多かった子供たちが、表を縦で見ることに気付けるようにします。そこで、板書や１人１台端末を活用します。提示した表に矢印（→）を書き、数値の変化を書き込むことで、ｘとｙの関係性に気付くきっかけとなります。そして、子供たちは、対応のきまりに気付き、どのように式に表すことができるのか考えていきます。
本時の展開
この直方体の形をした水槽に、水を入れていきます。
※動画を視聴する。
２分経ちました。水槽の水の深さは４cmになっています。
（表に記入する）
さらに水を入れていきますよ。４分経ちました。水槽の水の深さは何cmになっていますか。
（動画を止める）
物差しを見ると、８cmのところまで水が入っていることが分かります。
（表に記入する）
６分後や８分後は、水槽の水の深さは何cmになっていると思いますか。
６分後は、12cmになっていると思います。
私も12cmだと思います。
どうして12cmだと思ったのですか。
表を横に見ました。時間が２分から４分に、２倍になっています。それに伴って、深さも４cmから８cmに、２倍になっています。だから、時間が２分から６分に、３倍になると、それに伴って、深さも３倍になって、４cmの３倍で12cmになります。
つまり、水を入れる時間と水の深さは、比例の関係になっています。だから、時間が２分から８分に、４倍になると、それに伴って、深さも４倍になって、４cmの４倍で16cmになります。
賛成です。比例のきまりを使って考えればよいです。
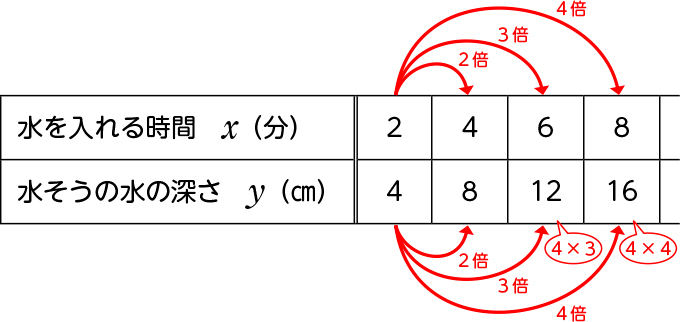
表を横に見て、比例のきまりを使ったのですね。では、動画の続きを見て、確かめてみましょう。
※動画を視聴する。
やっぱり、６分後は12cm、８分後は16cmになっていました。
比例の関係になっているから、計算で求めることができました。
では、水を入れる時間が13分のときは、水の深さは何cmになりますか。
水を入れる時間が13分のとき、水そうの水の深さは何cmになりますか。
え！ ⋯⋯難しいです。
どうして難しいと思ったのですか。
これまでは表を見て、２の整数倍を考えればよかったけれど、分数倍（倍）をしなくてはいけないから、求めることが大変だと感じました。
単純な整数であれば、表を見て考えやすかったけれど、整数倍でない場合は難しいです。
求めることが難しくないようにしたいけれど、どうすればよいかな。
５年生まで〇と□の関係を基に、〇と□の関係を表す式を使って求めていました。この考え方を生かすことはできませんか。
確かに使えそうです、でも、どんな式になるのかな。
さっきは、表を横で見ていたけれど、表を縦に見ると、他のきまりが見えてきそうです。
ｘとｙの関係を表す式を使えば、簡単に求められると思います。
ｘとｙの関係を式で表したいのですね。では、考えていきましょう。
ｙがｘに比例する場合、ｘとｙの関係を表す式を考えよう。
見通し
表を横に見て考えてみよう。
表を縦に見て考えてみよう。
表を縦に見て、いろいろな見方で式を立ててみよう。
自力解決の様子
Ａ つまずいている子
・表を横に見ることしかできず、ｘとｙの関係性に気付くことができていない。
Ｂ 素朴に解いている子
・表を縦に見て、どの数値の場合でも、「ｘを２倍すると、いつもｙになる」ことに気付いている。
Ｃ ねらい通り解いている子
・表を縦に見て、常に「ｙ÷ｘ＝２」であることに気付いている。
・「２」が何を表しているか考えている。
全体発表とそれぞれの考えの関連付け
みなさん、どのように求めましたか。
（Ａさん） 表を縦に見ると、ｘの値を２倍にすると、ｙの値になることに気付きました。
Ａさんと同じ考えです。例えば、ｘが２のとき、２倍すると、ｙは４になります。ｘが４のとき、２倍すると、ｙは８になります。
つまり、ｘとｙの式に表すと、どんな式になりますか。
「ｘ×２＝ｙ」です。ｘに２をかけると、いつもｙになります。
みなさんも、同じ式になりましたか？
（Ｂさん） 僕は、違う式になりました。「ｙ÷ｘ＝２」です。
（Ｃさん） え、どうして違う式になったのだろう？ どんな考え方をしたのかな。
違った式なので、ＣさんはＢさんの考え方が気になったのですね。どんな考え方をしたのですか。
（Ｂさん） 僕も表を縦に見たのですが、ｙをｘで割ると、いつも商が２になることに気付きました。
本当だ。例えば、ｙ＝４、ｘ＝２のとき、４÷２＝２です。ｙ＝８、ｘ＝４のとき、８÷４＝２です。
ｙ÷ｘの答えは、いつも２になります。
では、ｙがｘに比例するときは、「ｘ×２＝ｙ」「ｙ÷ｘ＝２」の２つの式ができるのですね。
よく考えると、「ｘ×２＝ｙ」と「ｙ÷ｘ＝２」は同じ式だと思います。
どういうことですか。
ｘとｙだと分かりにくいけれど、数字を入れてみると分かりやすいです。例えば、ｘ＝３だとしたら、ｘ×２＝ｙは３×２＝６で、ｙは６になります。もう１つの式にｘ＝３、ｙ＝６を入れてみると、ｙ÷ｘ＝２は６÷３で、２になります。
他の数字でも同じことが言えるのかな。
例えば、ｘ＝４だとしたら、ｘ×２＝ｙは４×２＝８で、ｙは８になります。もう１つの式にｘ＝４、ｙ＝８を入れてみると、ｙ÷ｘ＝２は８÷４で、２になります。
やっぱり、この２つの式は同じ式だと言えます。
２つの式を見比べたり、数字を当てはめて成り立つかどうか確かめたりして気付いたのですね。
ｙがｘに比例するとき、ｘの値でそれに対応するｙの値を割った商は、いつも決まった数になる。
ｙ÷ｘ＝決まった数
ｙをｘの式で表すと、次のようになる。
ｙ＝決まった数×ｘ
今考えている水を入れる時間と水の深さの比例関係の場合は、決まった数は２になります。
ｘとｙの値が変わっても、決まった数２は変わらないのですね。この「２」は、何を表しているのかな。
決まった数２が表していることを考えているのですね。
はい。私は、ｘ＝１のときのｙの値を表していると思います。今回の表は、ｘの値が２・４・６・８のときしか書かれていませんが、ｘ＝１も表に書くとすると、ｙの値は２になります。
そう考えると、決まった数２は、１分当たりに入る水の深さとも言えます。
私は、表を横に見て考えました。決まった数２は、ｘが１増えるときのｙの増える数量ということもできます。
決まった数２が何を表しているかよく分かりました。比例の関係にある２つの数量によって、決まった数は異なってくるのですね。
他の比例の関係にある２つの数量も式に表してみたいです。
そうですね。さて、水を入れる時間が13分の場合、水の深さは何cmになるのか求めてみましょう。
ｙ＝２×13になるので、26Ｌです。
「ｙ＝決まった数×ｘ」の式を使えば、簡単に求めることができました。
式を使えば、ｘの値がどんな数になっても、ｙの値を求めることができそうです。
まとめ
- ｙがｘに比例するとき、ｘの値でそれに対応するｙの値を割った商は、いつも同じ数になる。
→ｙ÷ｘ＝決まった数 - ｙをｘの式で表すと、ｙ＝決まった数×ｘ
- ｘとｙの関係を式で表すと、ｘの値に対応するｙの値を計算で簡単に求めることができる。
では、評価問題で、他の場面でも「ｘとｙの関係を表す式」を求めることができるか考えてみましょう。
評価問題
下の表は、自転車が進む時間と道のりの関係を表したものです。
①ｘとｙの関係を表す式を求めましょう。
②出発して19分で、進んだ道のりは何ｍですか。
子供に期待する解答の具体例
①ｙ＝200×ｘ
②200×19＝3800
3800ｍ
感想例
- ｙがｘに比例する場合、ｘの値でｙの値を割った商は、いつも同じ数になることが分かりました。
- 変化のきまりを使わなくても、「ｙ＝決まった数×ｘ」の式を使えば、簡単に求めることができました。もっと大きな数でも試してみたいです。
ポイント＆アドバイス
構成／桧貝卓哉 イラスト／横井智美 図版作成／永井俊彦