小５算数「合同な図形」指導アイデア《図形を１本の対角線で分けてできる三角形が、合同かどうか確かめる》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.07.30

単元の展開

第１時　図形を重ね合わせ、合同な図形について知る。
▼
第２時　合同な図形の対応する頂点、辺、角について調べる。
▼
第３時（本時）図形を１本の対角線で分けてできる三角形が、合同かどうか確かめる。
▼
第４時　合同な三角形をかくための条件について話し合う。
▼
第５時　合同な四角形をかくための条件について話し合う。

本時のねらい

前時までに着目してきた構成要素どうしの関係や、既知の図形の定義や性質を基に、四角形を１本の対角線で分けてできた図形が合同であるかについて筋道立てて説明する。

評価規準

四角形を１本の対角線で分けてできる２つの三角形が合同になるかについて、構成要素どうしの関係に着目して辺の長さや角の大きさを調べたり、既知の図形の性質を活用したりするなどして考え、説明している。

本時の展開

四角形を、１本の対角線を用いて２つの三角形に分けます。その２つの三角形は合同か、分かりやすく説明しよう。

まずは正方形から考えてみましょう。

簡単です。２つの三角形は合同です。

辺も角も調べてもいないのに、なぜ合同だと言えるのですか。

折り紙を折ったら、ぴったり重なるからです。

これまでの経験からそのように考えたのですね。では、どんな正方形でも言えますか。

そう言われると自信がなくなる。

たまたまかもしれない。

いや、言えるよ。正方形はすべての辺の長さが同じだから、２つの辺の長さが同じだよ。

２つとは、どこのことなの。

分かりにくいから、辺や角に名前を付けましょう。

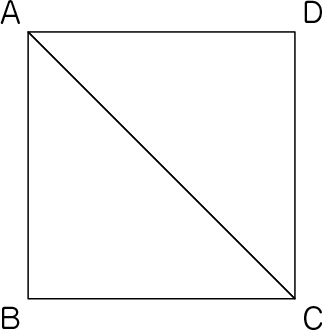
正方形は辺の長さがすべて同じだから、辺ＡＢ＝辺ＡＤ、辺ＢＣ＝辺ＤＣ、辺ＡＣはどちらにも共通だから３つの辺が同じ長さだよ。

正方形の角はすべて直角だから、角Ｂ＝角Ｄだね。

角ＢＡＣと角ＤＡＣは同じですか。

同じです。直角二等辺三角形だから、三角定規と同じです。だから45度で同じです。

だとすると、角ＢＣＡも角ＤＣＡも同じだね。

印をつけるとこのような感じですね。

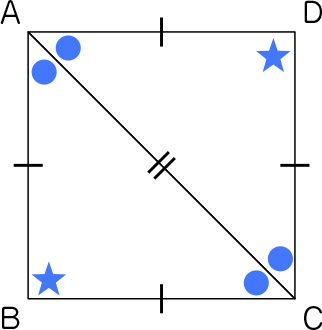
すごい！　１つも直接測らなくてもできた。

なぜ１つも直接測らなくてもできたのでしょう。

正方形のきまりや性質を使ったからです。

直角二等辺三角形の性質も使いました。

図形に印や名前を付けたから、分かりやすくなりました。

他の図形でもできそうな気がします。

図形のきまりや性質を使ったら、たまたまではなくて、どんな正方形でも言うことができますね。では、例えば平行四辺形も対角線で分けて、２つの三角形が合同かどうかについて説明することができますか。

正方形と違って、折っても重ならないね。

折っても重ならないということは、合同じゃないのかな。

きちんと調べてみないと分からないね。

さっきのように平行四辺形の辺や角に名前を付けて、合同かどうか調べてみよう。

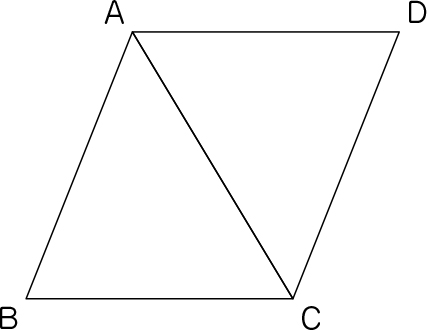
構成要素どうしの関係や既知の図形の定義や性質を基に、四角形を１本の対角線で分けてできる２つの三角形が合同であるか筋道立てて説明する。

見通し

対応する辺や角を調べればできそう。（方法の見通し）

平行四辺形のきまりや性質を使えばできそうだな。（方法の見通し）

折っても重ならないけど、合同になりそうね。（結果の見通し）

自力解決の様子

A　つまずいている子
構成要素の対応関係を捉えることができず、折っても重ならないので合同ではないと判断している。

Ｂ　素朴に解いている子
対応する辺の長さや角の大きさを、定規やコンパス、分度器を用いて直接調べている。

Ｃ　ねらい通り解いている子
平行四辺形のきまりや性質を使い、調べなくてもよいところは直接測らずに、対応する辺の長さや角の大きさを調べて合同かどうかを判断している。

学び合いの計画

本学習は、この後の学習の素地的経験を含んでいます。例えば、単元計画上で、次時には合同な三角形の作図を扱いますが、そこでは、いかに少ない条件で合同な三角形の作図ができるかを考えます。労力を減らして合同かどうかを判断しようと考えた経験は、次時に６つの条件すべてを使わないで効率的に作図しようとする経験につながります。そして、６年生では対称な図形を学習しますが、そこでの考察の際に今回の学習の経験が生きます。対称の軸で分けた２つの図形や、対称の中心と対応する頂点を結んだ線で分けた２つの図形は合同です。四角形を、１本の対角線を基に分け、その２つの図形どうしの関係を考察することは、その考察の際に重要な学習経験となります。

そこで本時の学習では、単に２つの図形が合同であるかどうかの考察の結果だけではなく、既知の図形の定義や性質を使って直接測定しなくてもよいところは測定しないで調べることで、労力を減らして考察する過程をていねいに扱いましょう。正方形と平行四辺形の考察の経験を生かし、他の四角形についても考察の範囲を広げていけるように、分かったことや見いだしたことを学習の途中でふり返って整理しながら発展的に考える意欲を醸成していくことが大切です。

学び合いの後半で、他の図形に考察の範囲を広げる際には１人１台端末の活用が有効となります。その際には、個々がどんな図形をどんな課題で取り組んでいるかを明らかにしましょう。例えば、どんな平行四辺形でも言えるか、例示されて平行四辺形とは違う形の平行四辺形をかいて考察している子供はより一般性を求めて考察しています。また、ひし形や長方形について考えている子供は、より考察の範囲を広げることを目的としています。１人１台端末を利用したことで、ただ使っているという状態やただ考えを集約しているという状態とならずに個の学びのヒントとなりうるように、どんな目的で何に取り組み、何が分かったのかが見えるように工夫をしていくことが必要です。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

＊Ｃ１、Ｃ２、Ｃ３それぞれ発表をする。

Ｃ１
図形を切って重ねて調べたら、三角形ＡＢＣと三角形ＣＤＡはぴったり重なるので合同です。

Ｃ２
平行四辺形を対角線で２つに分けたら、２つの三角形に分かれました。対応する辺の長さと角の大きさを定規や分度器で調べたら、すべて同じ長さや大きさでした。なので、三角形ＡＢＣと三角形ＣＤＡは合同です。

Ｃ３
平行四辺形の向かい合う辺の長さは同じなので、辺ＡＢ＝辺ＣＤ、辺ＢＣ＝辺ＡＤです。辺ＡＣはどちらにも共通です。角の大きさは分度器で調べました。すると、対応するすべての角も等しいので、２つの三角形は合同です。

３つの考えを見比べてみて、どれがよりよいですか。

Ｃ３さんの考え方が直接調べなくていいから楽だね。

Ｃ１さんのほうがぱっと分かって楽だよ。

でも、切って重ねられるときしか使えないよ。

図形が手元にあるときしか使えない。

でも、切って調べられるときには手軽だね。

ハサミを使うのが苦手だから、あまり使いたくないな。

切るときに線が曲がると、きちんと調べられないね。

そう考えると、Ｃ２さんのようにきちんと測って調べると確実だよ。

でも、６個も測るのはめんどくさいな。

そうなると、Ｃ３さんの考えが調べるところが少なくて楽だね。

Ｃ３さんの考えのなかでも、調べなくてもいいところがあるよ。

え？　どこのこと？

平行四辺形なら、向かい合う角の大きさも同じだから、角Ｂと角Ｄも測らなくても同じだよ。

確かに。そこもいちいち測らなくてもいいね。

図形のきまりや性質を使うとやっぱり便利だね。

２人の考えから、三角形ＡＢＣと三角形ＣＤＡは合同だということが分かりますね。正方形の場合と比べてみると、どんなところが同じで、どこが違いますか。

対応するすべての辺の長さや角の大きさが同じということは共通しています。

どちらも合同な三角形に分かれました。

図形のきまりや性質を使って調べているところも同じです。

違うところで、当たり前だけど、正方形には直角があって、平行四辺形には直角がないね。

正方形はすべて図形のきまりや性質で合同であるかどうかを説明できたけど、平行四辺形では２か所だけ測らないといけなかった。

辺の長さは全部図形のきまりや性質で分かったね。

角度にもこのようなきまりがあったらいいのになぁ。

三角形どうしを比べる場合、辺や角は全部でいくつありますか。

全部で６個です。

ということは、正方形は６個すべて図形のきまりや性質で調べることができて、平行四辺形の場合には６個のうち２個だけ直接調べればよかったのですね。調べた結果、正方形の場合も平行四辺形の場合も、合同な三角形に分かれることが分かりましたね。

他の四角形も合同な図形に分かれるのかな。

いろいろ調べてみたいな。

もう少し図形のきまりや性質を使って考えてみたい。

平行四辺形も形を変えてみて、どれも本当に合同になるか調べてみたい。

そのときも２か所の角度だけ調べればいいね。

逆に、合同な図形に分かれない四角形はあるでしょうか。

台形はならないと思う。見た目でなんとなく分かる。

ひし形は合同な図形に分かれそう。

名前のないふつうの四角形はならない。

でも調べてみないと分からないよ。

他の四角形ではどうなのかなと、新たにやってみたいことが生まれましたね。１人１台端末に先生が用意した図形がありますし、自分で図形をかいて調べてもかまいません。他の四角形も対角線で合同な図形に分かれるか調べてみましょう。これまで学習した図形を扱うときには、せっかく今日便利だと分かった図形のきまりや性質を使ってみましょうね。

四角形のなかには、対角線で分けると合同な三角形に分かれるものがある。図形のきまりや性質を使うと、直接測らなくてよいところがあって便利だ。