小３算数「分数」指導アイデア《同分母分数の加法と減法の計算方法を考える》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.03.12

単元の展開

第１時　分数の意味に着目して、等分した長さの表し方を考える。
▼
第２時　単位分数の個数に着目して、分数を用いた長さの表し方を考える。
▼
第３時　分数を用いた長さの表し方に着目して、分数での体積の表し方を考える。
▼
第４時　１目盛りの大きさに着目して、分数を数直線に表す方法を考える。
▼
第５時　単位分数に着目して、１より大きい分数の表し方を考える。
▼
第６時　基の大きさに着目して、[MATH]\(\frac{3}{4}\)[/MATH]ｍと基の長さの[MATH]\(\frac{3}{4}\)[/MATH]の長さの違いを考える。
▼
第７時　0.1や[MATH]\(\frac{1}{10}\)[/MATH]は１を何等分しているかに着目して、分母が10の分数と[MATH]\(\frac{1}{10}\)[/MATH]の位までの小数の関係について考える。
▼
第８時　分数の仕組みに着目して、分数の加法の計算方法を考える。
▼
第９時　分数の仕組みに着目して、分数の減法の計算方法を考える。
▼
第10時　まとめ

本時のねらい

分数の表し方と仕組みに着目し、同分母分数の加法及び減法の計算方法を考え、説明することができる。

評価規準

単位分数の何個分かに着目し、整数と同じように同分母の分数の加法計算ができることを式や図を用いて考え、説明している。（思考・判断・表現）

本時の展開

ジュースが、大きいびんに[MATH]\(\frac{3}{10}\)[/MATH]L、小さいびんに[MATH]\(\frac{2}{10}\)[/MATH]L入っています。合わせて何Lありますか。

どんな式を立てればいいでしょう。

[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]です。

どうしてたし算ですか。お隣の友達に説明してみましょう。

※説明し合う。

どのように説明しましたか。

「合わせる」からたし算です。

（動きで表して）こんなふうに合体させるからたし算です。

そうですね。たし算ですね。今日は同じ分母の分数のたし算の仕方を考えていきましょう。

同じ分母の分数のたし算の仕方を考えよう。

では、[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]の計算の仕方を考えましょう。答えを出すだけではなくて、どうしてそのように計算できるのか図や言葉でも説明してみましょう。

自力解決の様子

A　つまずいている子
・分子と分母、それぞれをたし算している。
[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]＝[MATH]\(\frac{5}{20}\)[/MATH]

Ｂ　素朴に解いている子
・分子だけを計算する理由の説明が不十分。
10は分けた数だから足さずに[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]＝[MATH]\(\frac{5}{10}\)[/MATH]
・小数にして計算している。
[MATH]\(\frac{3}{10}\)[/MATH]＝0.3、[MATH]\(\frac{2}{10}\)[/MATH]＝0.2だから、0.3＋0.2＝0.5

※自力解決中に、学習したことを使って解決したことを価値付けつつ、分数のまま計算することはできないか問いかける。

Ｃ　ねらい通り解いている子
・図を使って説明している。
目盛り３個と２個だから５個になって、[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]＝[MATH]\(\frac{5}{10}\)[/MATH]

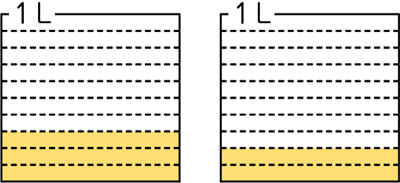
・言葉で説明している。
[MATH]\(\frac{1}{10}\)[/MATH]が３個と２個だから、[MATH]\(\frac{1}{10}\)[/MATH]が５個。[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]＝[MATH]\(\frac{5}{10}\)[/MATH]

ノート例

B　素朴に解いている子

A　つまずいている子

全体発表とそれぞれの考えの関連付け

答えが分かれましたよ。[MATH]\(\frac{5}{10}\)[/MATH]Lと答えた人と[MATH]\(\frac{5}{20}\)[/MATH]Lと答えた人がいました。自分の答えとは違うほうの人が、どうしてそのような答えを出したか分かりますか。

[MATH]\(\frac{5}{20}\)[/MATH]Lと答えた人は、分母の10＋10をして、分子の３＋２をして、[MATH]\(\frac{5}{20}\)[/MATH]になったのだと思います。

[MATH]\(\frac{5}{10}\)[/MATH]Lと答えた人は、分子の３＋２だけをして、[MATH]\(\frac{5}{10}\)[/MATH]になったのだと思います。でも、どうして分母をそのままにしたのか分かりません。

分母の10は分けた数だから、足さなくていいと思います。

図にかくと、こうなります。[MATH]\(\frac{2}{10}\)[/MATH]Lのジュースをこちらに入れると、目盛り２つ分増えるから[MATH]\(\frac{5}{10}\)[/MATH]だと思います。

確かに。

この1目盛りは、[MATH]\(\frac{1}{10}\)[/MATH]Lだから、[MATH]\(\frac{1}{10}\)[/MATH]が３つと２つだから[MATH]\(\frac{1}{10}\)[/MATH]が５つになるので[MATH]\(\frac{5}{10}\)[/MATH]です。

〈Ｃ１〉でも、図を見ると目盛りは20個あります。20個に分けられているから、1つの目盛りは[MATH]\(\frac{1}{20}\)[/MATH]Lだと思います。

なるほど。確かに目盛りは20個ですね。Ｃ１さんのお話についてどう考えるか、隣りの人とお話ししましょう。

これは、[MATH]\(\frac{3}{10}\)[/MATH]です。ということは、この1目盛りは[MATH]\(\frac{1}{10}\)[/MATH]Lです。入れ物が２つになったからといって、1目盛りが[MATH]\(\frac{1}{10}\)[/MATH]Lから[MATH]\(\frac{1}{20}\)[/MATH]Lにはならないと思います。

[MATH]\(\frac{1}{10}\)[/MATH]Lというのは、１Lを10等分したものが１つ分です。入れ物が２つになっても、１Lは10等分されているから、1目盛りは[MATH]\(\frac{1}{10}\)[/MATH]Lです。

そうでしたね。[MATH]\(\frac{1}{10}\)[/MATH]Lは１Lを基にしているのでしたね。1目盛りは[MATH]\(\frac{1}{10}\)[/MATH]Lですね。Ｃ１さんがお話ししてくれたので、みんなもしっかりと確認することができましたね。Ｃ１さん、納得できましたか？

〈Ｃ１〉納得しました。1目盛りが[MATH]\(\frac{1}{10}\)[/MATH]Lだから、[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]＝[MATH]\(\frac{5}{10}\)[/MATH]だと分かりました。

[MATH]\(\frac{3}{10}\)[/MATH]＋[MATH]\(\frac{2}{10}\)[/MATH]は、[MATH]\(\frac{1}{10}\)[/MATH]が３つと２つだから３＋２の計算で考えることができるのですね。こんなふうに考えていた人がいましたよ。0.3＋0.2＝0.5。どのように考えたか、分かりますか。

[MATH]\(\frac{3}{10}\)[/MATH]は0.3と同じで、[MATH]\(\frac{2}{10}\)[/MATH]は0.2と同じです。だから0.3＋0.2で計算したのだと思います。

分数＋分数だとまだ学習していなかったから、小数にして計算したのだと思います。

答えの0.5を分数にすると[MATH]\(\frac{5}{10}\)[/MATH]だから、答えは同じです。

そうですね。0.3＋0.2という小数の計算は前に学習しましたね。どうやって計算するのでしたか。

0.1が３個と２個だから、３＋２＝５で0.5です。

分数で計算するときも同じです。

どういうことですか。

小数のときは、0.1がいくつかを考えて３＋２になりました。今日は、[MATH]\(\frac{1}{10}\)[/MATH]が３つと２つだから３＋２なので、同じだと思いました。

小数は0.1を基にしていて、分数は[MATH]\(\frac{1}{10}\)[/MATH]を基にしたのですね。小数も分数も基となるもののいくつ分で考えれば、３＋２のように整数の計算にできるのですね。

評価問題

では、次の問題を解いてみましょう。そして、どうしてそのように計算できるか説明しましょう。隣どうしで説明し合ってみましょう。

ジュースが、大きいびんに[MATH]\(\frac{2}{4}\)[/MATH]L、小さいびんに[MATH]\(\frac{1}{4}\)[/MATH]L入っています。合わせて何Lありますか。

子供に期待する解答の具体例

＜Ｂ評価＞　
・[MATH]\(\frac{2}{4}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]＝[MATH]\(\frac{3}{4}\)[/MATH]　答え[MATH]\(\frac{3}{4}\)[/MATH]L　
・[MATH]\(\frac{1}{4}\)[/MATH]が２つと１つだから２＋１＝３で[MATH]\(\frac{3}{4}\)[/MATH]　答え[MATH]\(\frac{3}{4}\)[/MATH]L

＜Ｃ評価＞　
・計算はできているが理由を説明することができていない。または、正しく計算することができていない。

「隣の友達の説明が上手だったよ」という人、どんなところが上手だったのか紹介してください。

〈Ｃ３〉Ｃ２さんの説明が上手でした。図をかいて説明してくれました。

ではＣ２さん、みんなにも説明してください。

〈Ｃ２〉式は、[MATH]\(\frac{2}{4}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]です。[MATH]\(\frac{2}{4}\)[/MATH]と[MATH]\(\frac{1}{4}\)[/MATH]は図にかくとこうなります。1目盛りは[MATH]\(\frac{1}{4}\)[/MATH]で、目盛りが２＋１だから[MATH]\(\frac{3}{4}\)[/MATH]になります。Ｃ３さんも上手に説明してくれました。何のいくつ分という言葉で分かりやすかったです。

では、Ｃ３さんもお願いします。

〈Ｃ３〉式は、[MATH]\(\frac{2}{4}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]で、[MATH]\(\frac{1}{4}\)[/MATH]を基にすると[MATH]\(\frac{2}{4}\)[/MATH]は２つ、[MATH]\(\frac{1}{4}\)[/MATH]は１つだから、２＋１で[MATH]\(\frac{1}{4}\)[/MATH]が３つです。だから[MATH]\(\frac{3}{4}\)[/MATH]Lです。

今日の学習で分かったことをまとめましょう。

学習のまとめ

分数のたし算は、[MATH]\(\frac{1}{〇}\)[/MATH]を基にして、そのいくつ分かを考えれば、計算することができる。

感想例

初めは分母もたし算して[MATH]\(\frac{5}{20}\)[/MATH]Lかと思っていましたが、図の説明を聞いて、分母は足さなくてよいことが分かりました。
[MATH]\(\frac{1}{〇}\)[/MATH]を基にして考えれば、分数のたし算も整数のたし算でできることが分かりました。
ひき算も同じように考えればできると思うので、次回ひき算についてみんなと学習したいです。

イラスト／横井智美

【関連記事】

1人1台端末時代の｢教科指導のヒントとアイデア｣シリーズはこちら！