小6算数「多角形と対称」指導アイデア《四角形の線対称性と点対称性を調べて分類しよう》
執筆/埼玉県公立小学校教諭・播元和貴
編集委員/国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
(本時9/ 12)
ねらい
主な基本的な図形の対称性を調べることを通して、既習の図形に対する見方を深める。
評価規準
対称という観点から、図形を分類整理したり、性質を説明したりすることができる。(数学的な考え方)
問題
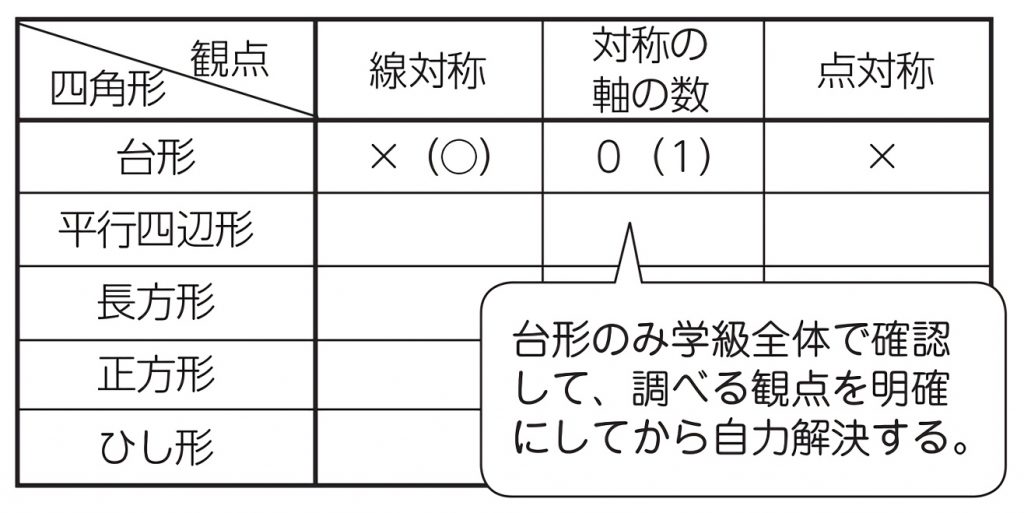
下の5つの四角形について、線対称な図形か点対称な図形かを調べましょう。
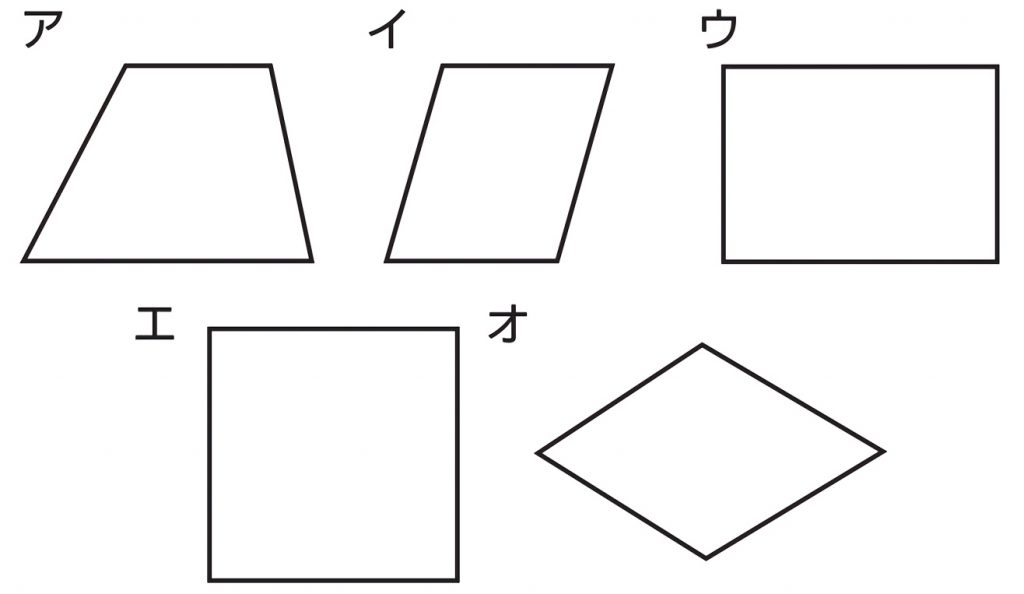
ア~オまでの四角形の名前を答えましょう。
アが台形、イが平行四辺形、ウが長方形、エが正方形、オがひし形です。
そうですね。今日は、これらの四角形を対称という観点で調べていきます。調べたことを表にまとめていきましょう。
本時の学習のねらい
これまでに学習した四角形を対称に着目して調べよう。
自力解決
どのように調べましょうか。
元の図形を写して、折ったり回転したりしてできそうです。
辺の長さや角の大きさを調べて、対称の軸が描けそうかを調べます。
対応すると思われる点どうしを結んで、交わったところが対称の中心かどうかを調べます。
A つまずいている子
・調べる観点が分からない。
B 素朴に解いている子
・図を写し取り、折ったり回転させたりして、線対称や点対称を確かめている。
C ねらい通りに解いている子
・具体物操作に加え、調べたことを図形の構成(ここでは辺の長さ、角の大きさ)や性質と関連付けて考えている。
学び合いの計画
ここでは、これまでに学習した四角形を「線対称」「点対称」という観点で調べ、図形の見方を深めることがねらいです。自力解決では、元の図形をトレーシングペーパーや透明シート等に写し取り、折ったり回転させたりすることが主な活動になると考えられます。一方で、辺の長さや角の大きさを意図的に設定しておくことで、折ったり、回転させたりするだけでなく、図形の構成に着目して考えることも、説明する際の根拠の1つにすることができます。
イラスト/横井智美
『小六教育技術』2018年4月号より