６年生　「分数のわり算」【「算数つまずき防止」ここがポイント！#７】

算数は一つつまずくと、その後の学習が進みにくくなる教科ですが、どのような授業づくりをすれば、つまずきを防止できるのでしょうか。今回は６年生「分数のわり算」の内容を、青森県六戸町立六戸小学校・田中宏一教諭に伺いました。

監修／弘前大学教授・中野博之

学習の過程全体で既習・既有の知識を生かしていく

６年生の算数で、最もつまずきが起きやすい単元は、「分数のわり算」だと思います。この単元については、指導する先生方も、どのようにして理解させるべきか悩まれる方が多いところだと思います。

この学習で、なぜ分数のわり算は×逆数になるのかをちゃんと理解していないと、分数のかけ算はそのままで、わり算は逆数で、ということがごちゃごちゃになってしまいます。そのため、分数と小数、かけ算とわり算が混在する、[MATH]\(\frac{3}{5}\)[/MATH]×[MATH]\(\frac{1}{4}\)[/MATH]÷0.8＝　というような問題があると、わけが分からなくなってしまうのです。それが、中学校の学習や高校受験にまで影響を与えるわけで、この「分数のわり算」が６年生の算数では難易度が高い単元だと思います。

この「分数のわり算」につながる単元は、「分数×整数」から入って、「分数×分数」を学習した後、「分数÷整数」「分数÷分数」と学習が進んでいきます。子供たちが「分数のわり算」を理解するためには、この「分数×整数」からの学習の流れを大事に押さえ、既習や既有の知識を生かしながら、考える過程を大事にしていくことが大切です。

ここから実際に以前の授業で私が押さえていったことを説明していきましょう。

「分数×整数」では、まず同数累加を学習しますが、例えば、[MATH]\(\frac{4}{5}\)[/MATH]×２ならば[MATH]\(\frac{4}{5}\)[/MATH]が2つ分ですから、子供たちはすぐに[MATH]\(\frac{4}{5}\)[/MATH]＋[MATH]\(\frac{4}{5}\)[/MATH]と図で表すことができます。「では、何が増えたの？」と問うと、「分子の数が増えました」と答えます。「分子の数はどうなったの？」とさらに問うと、「[MATH]\(\frac{4}{5}\)[/MATH]が2つ分になった」と言い、それは、[MATH]\(\frac{4×2}{5}\)[/MATH]と表すことができるということになります。そこから子供たちは、「分数×整数」は分子に整数をかけると答えが出せることに気付き、図と式が一致して納得します。

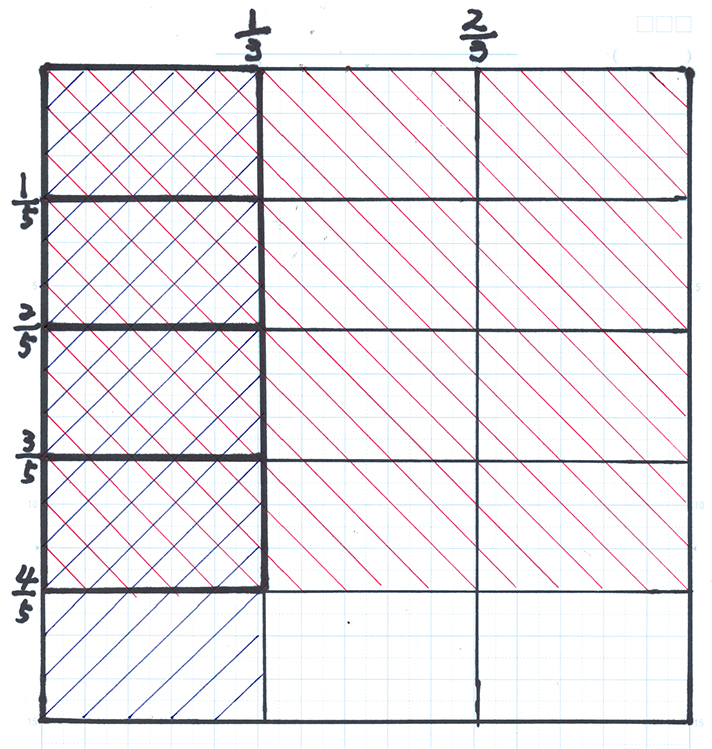
その次に「分数×分数」の学習で、[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]は、どうやればよいかを考えるときに、私は折り紙を使って授業をしました（資料１参照）。[MATH]\(\frac{4}{5}\)[/MATH]は、まず横折りで５等分して、そのうちの４つ分に色を塗ります。次に、「×[MATH]\(\frac{1}{3}\)[/MATH]だから、３つに分けたものの１つ分だよね」ということになって、その折り紙を縦に３等分に折ってそのうちの１つ分に色を塗ります。そこで、全体が小さく15等分されたものであることと、両方が重なった部分が４つあることが分かります。それで[MATH]\(\frac{4}{15}\)[/MATH]ということが分かって、「結局、分数のかけ算は[MATH]\(\frac{分子×分子}{分母×分母}\)[/MATH]になる」ということが分かります。

続けて「分数÷整数」の学習ですが、例えば「[MATH]\(\frac{4}{5}\)[/MATH]÷２はどうなるかな？」と投げかけると、子供たちは「[MATH]\(\frac{4}{5}\)[/MATH]を2つに分けるのだから、[MATH]\(\frac{2}{5}\)[/MATH]が2つになって、１人分は[MATH]\(\frac{2}{5}\)[/MATH]になる」と言います。そして子供たちのなかから「先生、これ分数のかけ算のときと同じだ！」と発見した声が上がります。つまり「[MATH]\(\frac{分子÷整数}{分母}\)[/MATH]で、分子をわればいい」ということに気付くのです。このときの２は[MATH]\(\frac{2}{1}\)[/MATH]ですから、この整数のわり算の考え方を生かせば、[MATH]\(\frac{4}{5}\)[/MATH]÷２＝[MATH]\(\frac{4}{5}\)[/MATH]÷[MATH]\(\frac{2}{1}\)[/MATH]＝[MATH]\(\frac{４÷２}{５÷１}\)[/MATH]となっており、「分母は分母、分子は分子でわっている」ということが考えられ、分数÷整数の考え方が分数÷分数の考えた方へと拡張されるわけです。

「分数÷整数」の学習は一歩先へ進み、「でも、分子をわるときに、整数にならなかったらどうすればいいんだろうね？」と投げかけ、[MATH]\(\frac{3}{4}\)[/MATH]÷２というような問題について考えていきます。すると子供たちは「先生、３÷２＝1.5だから、[MATH]\(\frac{1.5}{4}\)[/MATH]にすればいい」と言うのです。そこで「分子が整数じゃないけど、どうするの？」と問い返すと、「じゃあ、通分すればいい」と言い、「分子と分母を10倍にして、[MATH]\(\frac{15}{40}\)[/MATH]となり、約分して[MATH]\(\frac{3}{8}\)[/MATH]になる」と解決していきます。

ここでさらに、ある子供が「先生、分子が循環小数になったらどうすればいいんですか？」と問いを投げます。すると子供たちの間で、「確かに、分子が例えば、１÷３や１÷７になったら循環小数になって、さっきの方法は使えない」という話になります。そこで、みんなで[MATH]\(\frac{2}{7}\)[/MATH]÷３について考えていくことにします（画像１参照）。一人の子供が「先生、÷３が邪魔だから、÷３を消したい」と言い出します。子供たちは５年生のときに相殺の考え方を学習していますから、相殺して消そうということになります。そこで、「分子を１÷３×３にしよう」となるのですが、分子だけ３倍すると同じではなくなってしまいますから、「通分の考え方で分母も３倍すればいい」と言い、[MATH]\(\frac{２÷３×３}{７×３}\)[/MATH]という式が出てきます。そのようにして、子供たちは分数のかけ算で出てきた考え方を生かして、分数のわり算も解決していくのです。

その次のステップは「分数のわり算」を考えていくのですが、子供たちは分数÷整数の学習から、「分数のわり算」は[MATH]\(\frac{分子÷分子}{分母÷分母}\)[/MATH]でできると分かっています。そこで、分母も分子もわりきれない[MATH]\(\frac{5}{7}\)[/MATH]÷[MATH]\(\frac{2}{3}\)[/MATH]という問題では、どうしたらよいかを考えていきます（画像２参照）。[MATH]\(\frac{５÷２}{７÷３}\)[/MATH]は、分母も分子も整数にはなりません。そこで、子供たちはこれまでの学習を生かして、分母と分子にある÷３と÷２の両方を相殺していきます。すると、[MATH]\(\frac{５÷２×３×２}{７÷３×３×２}\)[/MATH]となり、[MATH]\(\frac{5}{7}\)[/MATH]÷[MATH]\(\frac{2}{3}\)[/MATH]＝[MATH]\(\frac{５×３}{７×２}\)[/MATH]＝[MATH]\(\frac{15}{14}\)[/MATH]となっていきます。

このように学習の過程で、新たに得た知識や既有の知識を結び付けながら、子供たち自身が対話をしながら考え、解決していったわけです。

自分の知と他者の知を広げ、人生を豊かにするために学ぶ

こうした学習過程を経ると、子供たちに「分数のわり算」がストンと落ちたのです。この学習過程ではプリント類は使っておらず、授業と自主学習ノートだけだったのですが、すべての子供たちが理解できました。

ちなみに「分数÷分数のわり算」については、最終的に子供から「先生、これ×反対（逆数）になっている」という声が出てきました。それで、算数が得意な子供たちはすぐに、逆数をかける形で分数のわり算を計算するようになっていきました。しかし、算数が苦手な子は３学期の途中頃まで逆数を使わず、少々めんどうではありますが、相殺する形で計算をしていたのです。それは、５年生の頃から相殺（移項）することをていねいに学習し、計算過程でもそれを大事にしてきたことを使っていたわけです。しかし、自転車に乗り始めたときに補助輪を使って乗っていた子供が、次第に慣れてきて補助輪を外すように、次第に苦手な子供たちも逆数を使うようになっていったのです。

つまり、学習内容がむずかしくなったときに大事なのは、計算の手続の暗記ではなく、それまでに学習したことを生かし、学習内容を拡張し統合していくことだと思います。とくに算数が苦手な子は、計算の手続きだけを覚えると、使わない間に忘れてしまいます。だからこそ地に足を付けて、子供たちの理解を徐々に広げていくことが大事なのだと思います。

結局は、何を目的として算数を学んでいるかを先生がしっかり考えておくことが重要です。「分数のわり算」などをなぜやるのかと言えば、自分たちで算数をつくっていくことが根本にあるのだと思います。これは算数に限らず、あらゆる教育とは押し付けられるものではなく、自分で納得して、自分のなかにある自己知をどんどん広げていく、それを他者の知と結び付けて共有知にしていくものだと思います。それを続けていくことが自分の人生の形成や社会の形成につながっていくのです。だから、目先の計算ができるできないということが重要なのではないのです。

大事にしたいのは考え方であり、分からないものをみんなで議論しながら、「これはいけそうだね？」「いけたね」「これはたまたまかな？」「いや、たまたまではないぞ」と検証していく科学的な思考であり、態度だと思います。教えられるのではなく、そうやって一生懸命考えることを通し、自分たちで新たな知をつくっていく経験を積み重ねることが一番大事にしたいことだと思うのです。

ちなみに高学年の学習内容では、この6年生の「分数のわり算」のほかに、5年生の「割合」もむずかしいところですが、５年生でも学習した二重数直線図を使って比例の考え方を使えば、立式はできると思います。その立式ができていれば、まずOKというくらいに捉えてあげたほうが、算数が苦手な子供も苦しくならずに算数に取り組み続けられると思います。

※

私自身、若い頃には算数・数学教育がよく分かっていなくて、40歳を過ぎてから大学院に２年間通ったのです。そのときに、「なんのために算数・数学教育を行うのか」という本質について、多数の本を読み、多くの問題を解き、ほかの先生方と問題を解き合いながら考えました。その過程でようやく「分かるとはどういうことなのか」が見えてきたような状況です。ですから、ひと言で「授業はこうすればよい」とは言えません。

ただ先生方に伝えたいのは、ご自身も分かるようになるためにいろいろ試行錯誤したと思いますが、それは子供たちも同じですから、試行錯誤する大切さを伝えてほしいということです。また、授業は各教科で点数を取れるようになるために行うのではなく、多様に考えて自分の人生を豊かにするためにあるのだということです。それを念頭に置いていれば、授業はむずかしいものではなく、子供たちにとっても先生自身にとっても楽しいものになるのではないかと思います。

取材／矢ノ浦勝之