小5算数「平均」指導アイデア《測定値のなかに０がある場合の処理のしかた》
執筆／福岡教育大学附属小倉小学校教諭・本田龍一朗
監修／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
単元の展開
第１時 測定値の平均の意味を知り、求め方を考える。
▼
第２時（本時）測定値に０がある場合の平均の求め方と、平均が小数値になる場合について考える。
▼
第３時 部分の平均から全体を見積もる方法を考え、身の回りで平均が使われている場面を見付ける。
▼
第４時 部分の各平均から全体の平均を求める方法を考える。
▼
第５時 平均の活用について考える（１歩の歩幅の平均を調べ、およその距離を測る）。
本時のねらい
平均の意味に着目し、データの値のなかに０がある場合の処理のしかたを考え、表現する活動を通して、その平均を求めることができるようにする。
評価規準
データの値のなかに０がある場合の平均を求めることができる。（知識・技能）
５人のチームで的当てをしたら、次のような結果になりました。このチームでは、１人の平均でなん点取ったことになりますか。
この単元の導入では、４人チーム、５人チーム、６人チームで的当て大会を行うという場面で、各チームの得点をならして比べる活動を通して、平均の意味や求め方を学んでいます。
本時では、チームの得点のなかに０点がある場合の結果を提示し、チームのなかに０点の人がいたらどうすればよいのかと発問することで、０の処理をどうすればよいのかという問いを生起し、本時の学習のねらいとします。
前回の大会で、このような結果のチームがありました。
※問題場面を提示する。
５人のチームの結果ですね。
鈴木さんの得点は０点になっているよ。的に当たらなかったんだね。
平均を求めるときに、チームのなかに０点の人がいたら、どうすればいいでしょうか。
０点の人は、入れなければいいと思います。
本当に入れなくてよいのかな。
０があるときの平均は、どのようにして求めればいいのだろう。
今日は、それをみんなで考えましょう。
０があるときの平均の求め方を考えよう。
見通し
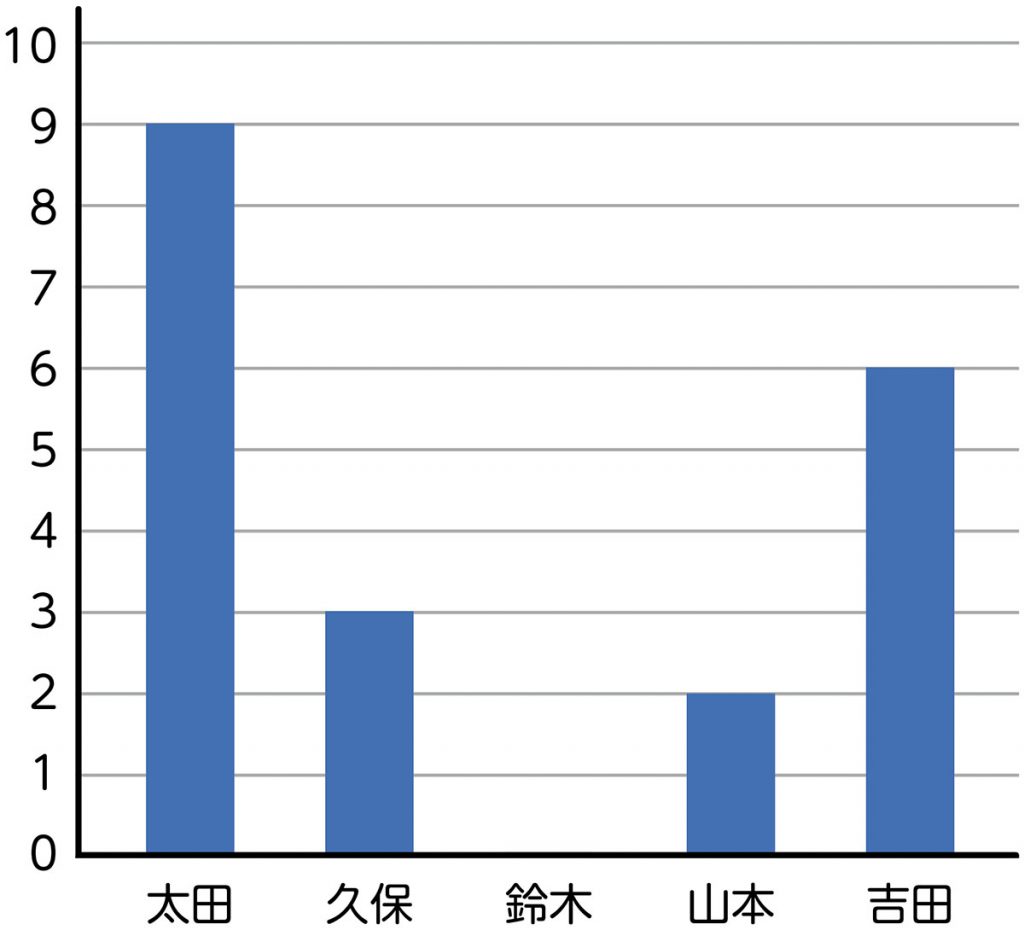
前時で学習した平均の意味に着目して、０を個数に含めるかどうかということについて自分の考えをもつことができるように、「平均は、どのようにすれば求めることができたか」と尋ね、平均＝合計÷個数で求められることを確認します。また、いくつかの数量を同じ大きさにならしたものが平均であるということを用いて考えることができるように、下のような棒グラフをICT環境（タブレット端末など）を活用して提示します。
この棒グラフの棒を１マスずつ操作してグラフの数量を同じ高さにならすことで、式だけでなく図や言葉を関連させながら説明するという見通しをもちます。
自力解決の様子
A つまずいている子
（９＋３＋２＋６）÷４＝５
５点
Ｂ 素朴に解いている子
（９＋３＋０＋２＋６）÷５＝４
４点
Ｃ ねらい通り解いている子
（９＋３＋０＋２＋６）÷５＝４
４点
チームの人数は５人なので、０点の「鈴木さん」も人数に入れて平均を求めるとよいと思いました。これを図で表して考えると、平均は４点になります。
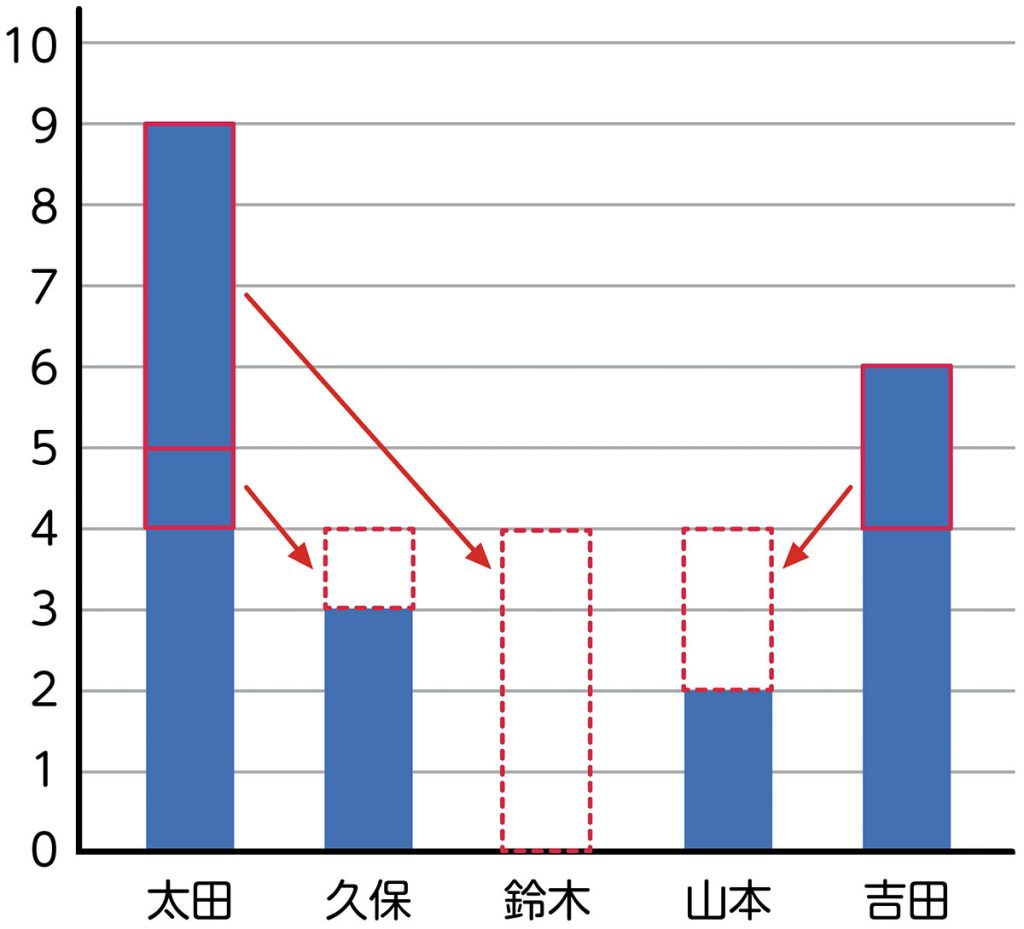
学び合いの計画
Ａは、０点の人を含めずに１チームの人数を４人として平均を求めています。Ｂは、既習の平均の意味に着目して、「鈴木さん」も的当て大会に参加したが０点であったという結果を踏まえ、人数に含めて計算しています。
イラスト／横井智美
-
小６体育「体の動きを高める運動【体つくり運動】」指導アイデア
-
小５体育「短距離走・リレー【陸上運動】」指導アイデア
-
小４体育「ゴール型ゲーム【ゲーム】」指導アイデア
-
小３体育「マット運動【器械運動】」指導アイデア
-
小２体育「体ほぐしの運動遊び【体つくりの運動遊び】」指導アイデア
-
小１体育「固定施設を使った運動遊び【器械・器具を使っての運動遊び】」指導アイデア
-
小４国語科「ヤドカリとイソギンチャク」全時間の板書＆指導アイデア
-
小１算数「たすのかな、ひくのかな」指導アイデア《たし算やひき算の演算》
-
小２算数「かけ算⑶」指導アイデア《９の段の九九の構成を通して、答えの増え方や交換法則に気付く》
-
小２算数「かけ算⑵」指導アイデア《物の数の求め方をかけ算を用いて解決する》
