小6算数「文字を使った式」指導アイデア《文字式が表す意味》
執筆/新潟県新潟市立上所小学校教諭・二瓶 亮
監修/文部科学省教科調査官・笠井健一
新潟県新潟市立新津第一小学校校長・間嶋 哲
単元の展開
第1時 xやaなどの文字を使った式の表し方を知る。
▼
第2時 文字に数を代入して、式の値を求める。
▼
第3時 乗法の場面を文字式で表し、文字に当てはまる数の求め方を考える。
▼
第4時 加法の場面を文字式で表し、文字に当てはまる数の求め方を考える。
▼
第5時 乗法や加法の混じった場面を文字式で表し、文字に当てはまる数の求め方を考える。
▼
第6時 場面や図と式を結び付けて、式を読み取る。
▼
第7時(本時)文字式にさまざまな数を当てはめ、図形と式を結び付けて、式が表す意味を考える。
▼
第8時 既習事項の確かめをする。
本時のねらい
文字式にさまざまな数を当てはめ、図形と式を結び付けて、式が表す意味について考えたり表現したりする。
評価規準
(a+b)×4÷2が表す図形について、aやbの条件を変えることでさまざまな図形の求積式になることを、図形と式とを結び付けて説明することができる。
問題
これまで皆さんはいろいろな図形の面積の出し方を学習しましたね。どんな図形がありましたか。
三角形や平行四辺形がありました。
ひし形や台形も学習しました。


文字式(a+b)×4÷2が表す図形はなんだろう。
高さが4㎝の台形です。五年生で公式を学習しました。
そうでしたね。では、自分でaとbに数値を当てはめ、図形をノートに書いて確かめてみましょう。
※子供が作成したものをタブレット端末で提出させて、教師が確認及び、全体に共有する。
ポイント
①台形の求積を表した式であることの共通理解を図る。
※文字式のどの文字や数値が、図形のどの部分に対応しているのかを確認する。
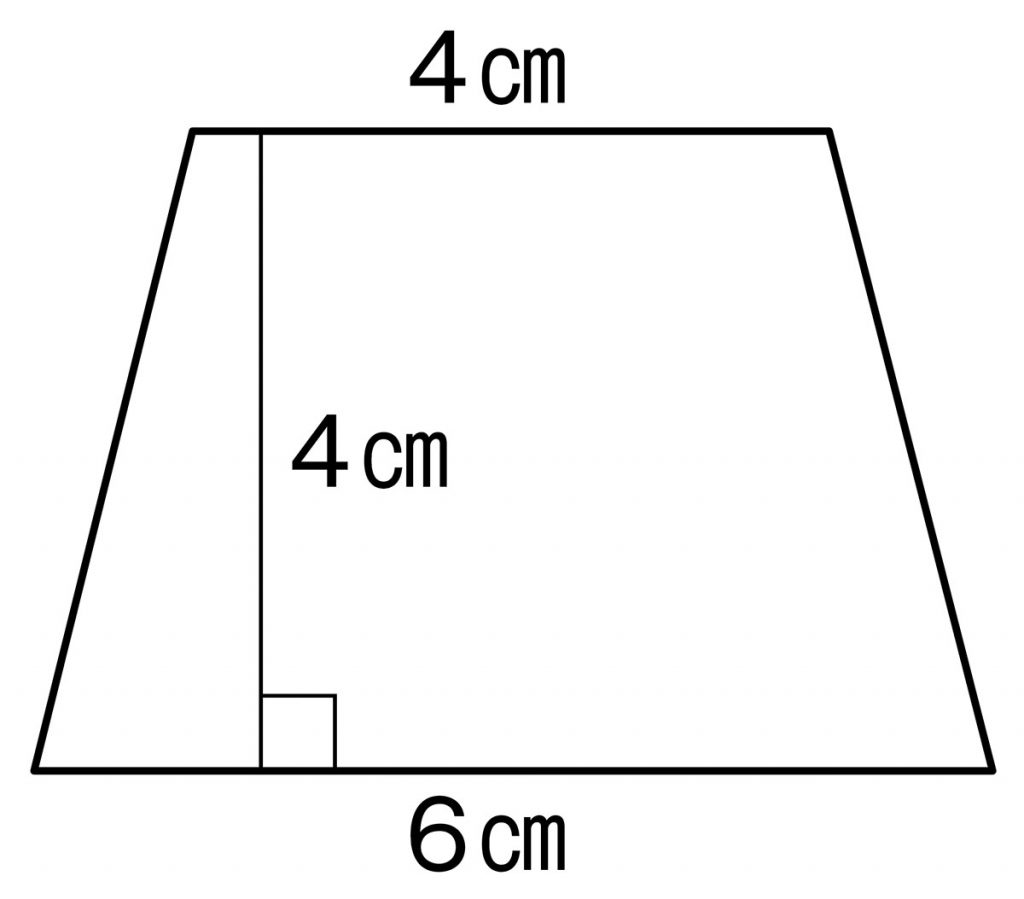
②上底もしくは下底の長さを極端に短い数値設定にした台形(子供が作成したものがあれば用いる)を提示することで、三角形に近付いていくことに気付かせる。
※段々と短くなっていくように提示することも効果的。
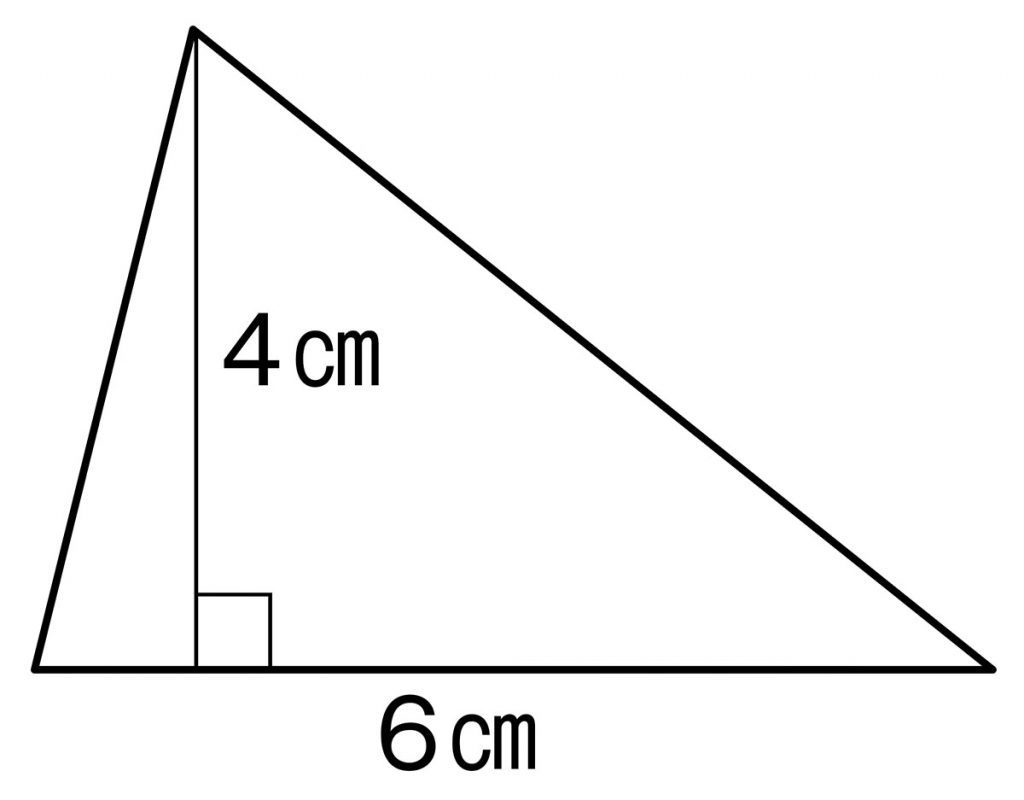
もしかして、この文字式は、三角形にもなるってことかな。
どうなれば三角形になりますか。
上底(下底)が0になればいいです。例えばa=0だったら、(0+6)×4÷2=6×4÷2となるから、底辺×高さ÷2で三角形の公式とも一致します。
だったら、ほかの図形でもできるんじゃないかな。

(a+b)×4÷2が表す図形は、台形や三角形以外にもあるのだろうか。
見通し
文字式のaとbの数値を変えると、どんな図形ができるか考えてみましょう。
長方形にできそうな気がします。
※実態に応じて、自力解決に入る前にできそうな図形を問い、「長方形にできそうか考えてみよう」などというように方向付けすることも考えられる。
自力解決の様子
A つまずいている子
a=bのとき、長方形(平行四辺形)になることをイメージし、作図することはできるが、図形と式とを結び付けることができず、「÷2」の扱いに困っている。
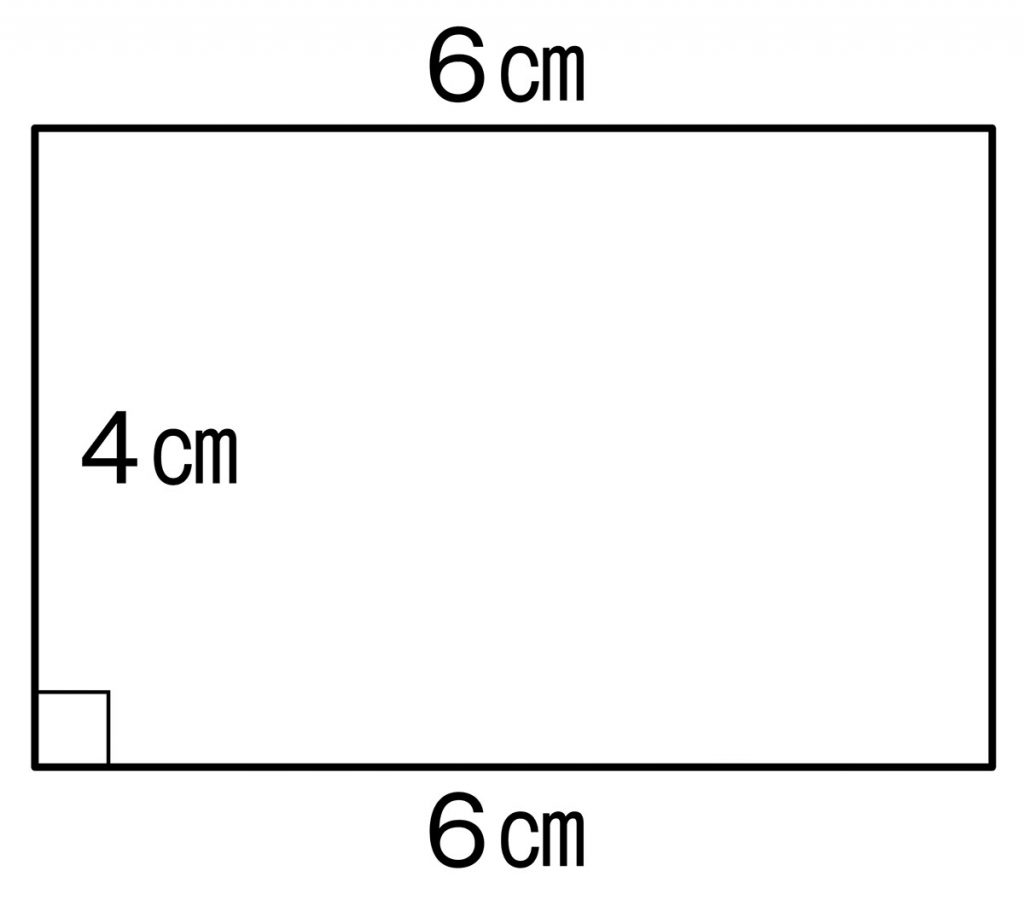
B 素朴に解いている子
a=bのとき、長方形(平行四辺形)になることをイメージし、式変形により、図形と式とを結び付けて考えている。
(6+6)×4÷2=12×4÷2=6×4

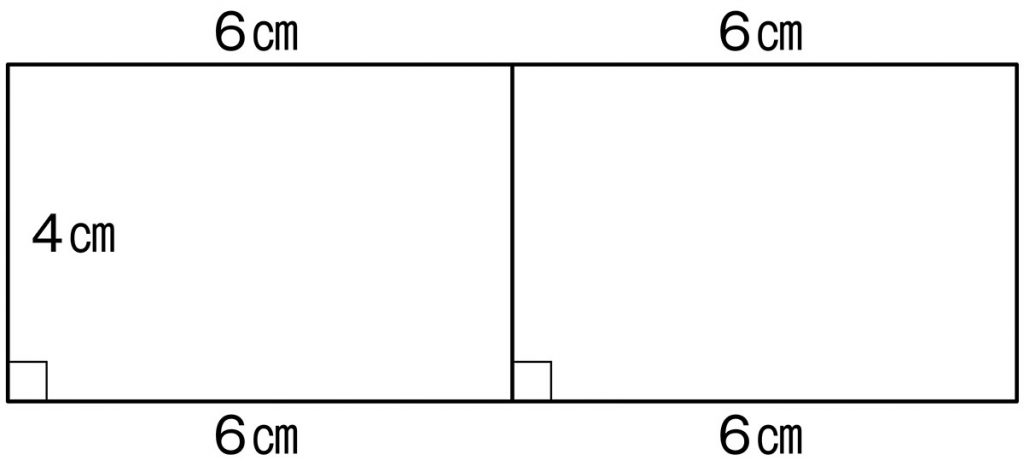
C ねらい通り解いている子
a=bのとき、長方形(平行四辺形)になることをイメージし、倍積変形により、図形と式とを結び付けて考えている。
(6+6)×4÷2=12×4÷2=6×4
学び合いの計画
イラスト/横井智美


