小6算数「角柱と円柱の体積」指導アイデア《三角柱の体積の求め方を考えよう》
執筆/東京都公立小学校教諭・横須賀咲子
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本時の位置 2/5
ねらい
角柱の体積の求め方を既習の考えを使って考え、説明することができる。
評価規準
角柱の体積の求め方を、既習の考えを使って説明したり、友達の考えた式を読み取ったりしている。
昨日は四角柱の体積の求め方を、改めて学習しましたが、体積は、どうやって求めることができましたか。
底面積×高さで求めることができました。
今日は、下のような三角柱の体積について考えていきましょう。
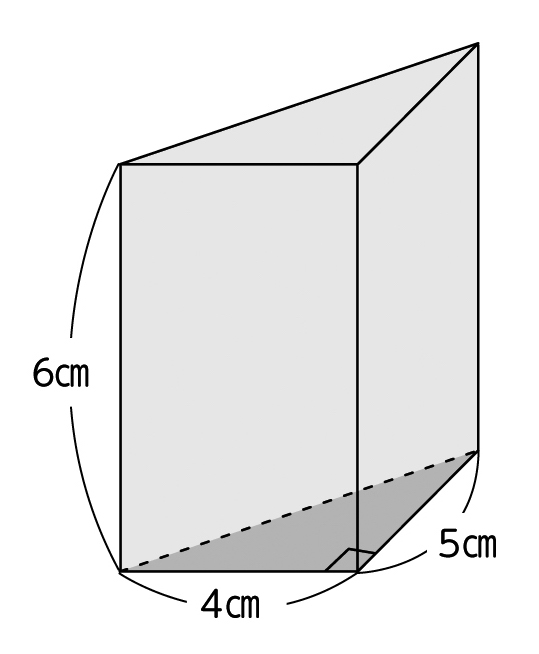
見通し
三角柱のときはどうすればいいのかな。
三角柱も、同じように底面積×高さで求められるのではないかな。
本時の学習のねらい
三角柱の体積も「底面積×高さ」で求められるのか考えてみよう。
上の三角柱の体積を求め、求め方を説明しましょう。
自力解決
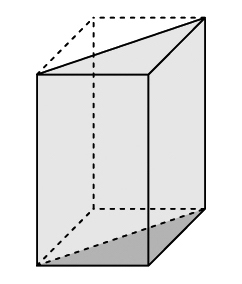
Aの考え
四角柱の半分の体積とみて5×4×6÷2=60
60㎤
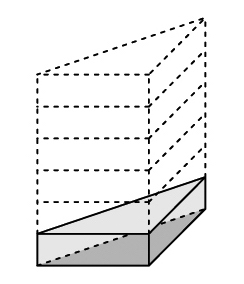
Bの考え
直方体の1段目が半分だから底面積が5×4÷2になってそれが6段あるから5×4÷2×6=60
60㎤
全体発表と関連付け
(A、Bの式のみを提示して)Aさん、Bさんはどのように考えたのでしょう。
Aさんの式の5×4×6は、たて5㎝、横4㎝、高さ6㎝の直方体の体積です。
それを÷2しているから、直方体の体積を求めてから、半分にして三角柱の体積を求めました。
直方体の体積(底面積×高さ)÷2になっています。
では、Bさんの式はAさんと比べてどうですか。
Bさん式は、Aさんと÷2の位置が違います。
Bさんはどのように考えたのでしょうか。
Bさんは底面の三角形の面積を求めてから6倍しています。
Bさんは三角柱の底面積を求めてから、高さをかけていると思います。
三角柱も底面積に高さをかけて体積を求めることができるのでしょうか。
三角形の底面積も高さ1cmの三角柱の体積と同じ数になって、その6倍を求めるのだからいいと思います。
四角柱のときと同じ考えだからいいと思います。
AさんとBさんの式を比べても、÷2の位置が違うだけで、Bさんの式はAさんの式と同じになるので三角柱も底面積×高さで求めていいと思います。
三角柱も底面積と1段目の体積は同じで、それが6段あるということだから、前回学習したように、底面積×高さで体積が求められるのですね。
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』2020年10月号より

