小3算数「たし算とひき算(筆算)」指導アイデア《たして500になる式をつくろう》
執筆/富山大学人間発達科学部附属小学校・屋鋪善祐
編集委員/文部科学省教科調査官・笠井健一、前・富山県公立小学校校長・中川愼一
目次
本時のねらいと評価規準
本時7/8時 3けたのたし算とひき算(筆算) のしかたを理解した後
本時のねらい
3けた+3けた=何百が成り立つ式について、繰り上がりのしくみに基づきながら筋道立てて考える。
評価規準
3けた+3けたの計算について、十進位取り記数法による数の表し方や十を単位として見る数の見方などを基に考えている。(思考・判断・表現)

問題場面
0から9の中から6枚選んで、たして500になる式をつくることはできそうですか。
(※一人ひとりに数カード10 枚を配付する)
すぐに全部の数を入れることは難しいな…。
十の位と一の位を0にするには、合わせて10になる数を考えればよいのかな。
どの位から考えればよいのだろう。
学習のねらい
たして500になる式のつくり方を考えよう。
見通し
大きい位の数から順番に考えていくとよさそうだ。〔方法の見通し〕
合わせて10 になる数を□に入れていけばよさそうだ。〔方法の見通し〕
百の位の数が5なので、1○○+3○○という式になりそうだ。〔結果の見通し〕
自力解決の様子
A つまずいている子
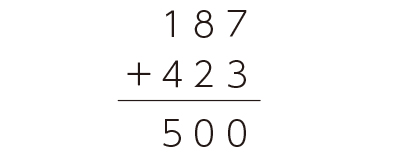
繰り上がりの数について考えていない。
B 素朴に解いている子
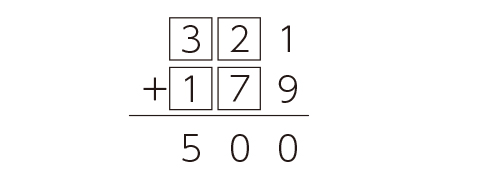
一の位から順に、式が成り立つ数の組み合わせを考えている。
C ねらい通り解いている子
十の位は、足して9になる数の組。
一の位は、足して10になる数の組。
「百の位はたして4になる数の組」「(0と4)も(2と2)もないので(1と3)」などと、筋道立てて考えている。
学び合いの計画
見いだした式を発表し合うだけでなく、「どうやって、この式を見付けたの」「どう考えたの」と問い返すことによって、考えの筋道や根拠を語る場を設けることが大切です。
イラスト/小沢ヨマ、横井智美
『教育技術 小三小四』2021年4/5月号より



