小3算数「わり算や分数」指導アイデア《紙テープを等分に切り分けた長さを求めるには》
執筆/板橋区立天津わかしお学校教諭・内藤信義
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 簡単な場合の何十÷1位数の計算の仕方について、既習の除法計算の仕方や数の構成を基に考え、説明する。
▼
第2時 簡単な場合の2位数÷1位数の計算の仕方を、既習の除法計算の仕方や数の構成を基に考え、説明する。
▼
第3時(本時)分数で表された数を除法の計算を用いて求めることができる。
▼
第4時 基の大きさが異なるものの等分した数について理解する。
本時のねらい
分数と除法について「等分する」という考えを用いて結び付け、分数で表された数を除法の計算を用いて求めることができる。
評価規準
等分することや分数の意味に着目して、分数で表されている場面について、除法を用いて計算することを考え、説明している。
本時の展開
本時では、「同じ大きさに分ける」ことを、「等分する」と表現することを知ります。「等分する」という表現は、教科書会社によって登場する場面が違いますが、ここでしっかりと言葉の確認をすることが大切です。
そして、等しく分けた1つ分の大きさを求める方法について、既習であるわり算と分数を関連付けながら考えていきます。
まずは、等分することを意識するために、あえて等分されていない状況から提示します。

紙テープを切り分けて、わかざりを作ろう。
(80㎝の紙テープの束を提示して)このような紙テープを切り分けて輪飾りを作りたいのですけど、先生が作ったらこんな感じになってしましました。

バラバラ。切り分けた長さが同じではないからです。
同じ長さになるように切り分ければきれいにできます。
きれいにそろった輪飾りにするには、どうすればいいのですか。
このテープを同じ長さに分ければいいです。
なるほど、同じ長さに分ければいいのですね。同じ大きさに分けることは「等分する」と言うのだけれど、それがきれいにそろった輪飾りを作るポイントなのですね。では、このテープを4等分するにはどうすればいいのでしょうか。
半分に折って、さらに半分に折ればいいです。
同じ長さに分けるのだから長さを測って、それを÷4すればいいです。
折って分ける方法と、計算で分ける方法がありそうですね。このように折って4等分に分けた1つ分の大きさを基の大きさの何と言えばいいですか。

基の大きさの[MATH]\(\frac{1}{4}\)[/MATH]です。
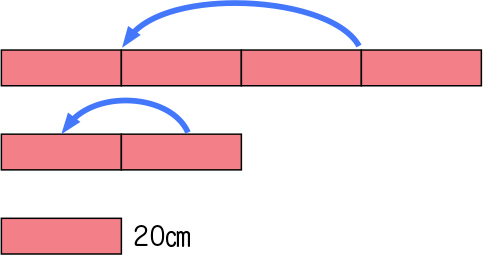
基の大きさを4等分した1つ分の大きさのことを[MATH]\(\frac{1}{4}\)[/MATH]と分数で表すこともできますね。この基の大きさにあたる紙テープは80㎝です。では、この80㎝の紙テープの[MATH]\(\frac{1}{4}\)[/MATH]の大きさは何㎝になるのでしょうか。


紙テープの長さは80㎝です。80㎝の[MATH]\(\frac{1}{4}\)[/MATH]の長さの求め方を考えよう。
見通し
どうやって考えますか。
わり算で計算します。
なるほど。さらにどうしてわり算が使えると思ったのかについて書けるといいですね。
実際に[MATH]\(\frac{1}{4}\)[/MATH]に折って長さを測ります。
なるほど。その場合は測った長さが基の長さの4等分になっているか、確かめることができるといいですね。
自力解決の様子
A つまずいている子
・4等分して長さを測るだけ
・式と答えだけ書いている
80÷4=20 答え20㎝
B 素朴に解いている子
紙テープを半分に折って、また半分に折って、長さを測ると20㎝でした。
20㎝が4つ分で20×4=80になるから、80㎝の[MATH]\(\frac{1}{4}\)[/MATH]の長さは20㎝。
C ねらい通り解いている子
80㎝の[MATH]\(\frac{1}{4}\)[/MATH]の長さは、4等分した1つ分ということだからわり算で求められる。
式 80÷4=20
10を基に考えると、10が8÷4=2で2つだから答えは20㎝。
学び合いの計画
80÷4の計算自体は前時までに学習しています。紙テープを[MATH]\(\frac{1}{4}\)[/MATH]の大きさに折って長さを測ることもできます。
そんななか、本時で重要なのは4等分してつくった[MATH]\(\frac{1}{4}\)[/MATH]の大きさは、わり算を使って求めることができるということをどのように結び付けるかにあります。
そのためには次のことを引き出します。
・[MATH]\(\frac{1}{4}\)[/MATH]は基の大きさを4等分した1つ分の大きさを表していること
・80cmを4等分した1つ分は80÷4で求めることができるということ
・[MATH]\(\frac{1}{4}\)[/MATH]の大きさにした20㎝を4倍(4つ分)すると80㎝になること
特に、基の大きさを4等分した1つ分の大きさを[MATH]\(\frac{1}{4}\)[/MATH]と表したことについては、第2学年で学習したことを思い出させ、定着が十分でない場合はしっかりと確認する必要があります。また、この既習事項が、わり算と分数を結び付けるキーワードでもあります。
4等分した1つ分の大きさを求めるにはわり算を使うことができることに気付かせ、4等分した1つ分の大きさである[MATH]\(\frac{1}{4}\)[/MATH]の大きさの20㎝は4倍すると基の大きさの80㎝になることを確認することで、それが正しいということを確かめることができます。
このような学習を通して、生活のなかでは操作として用いられることの多い[MATH]\(\frac{1}{2}\)[/MATH]や[MATH]\(\frac{1}{4}\)[/MATH]のような分数を「等分する」という視点で見直すことで、わり算と関連付けることが大切です。
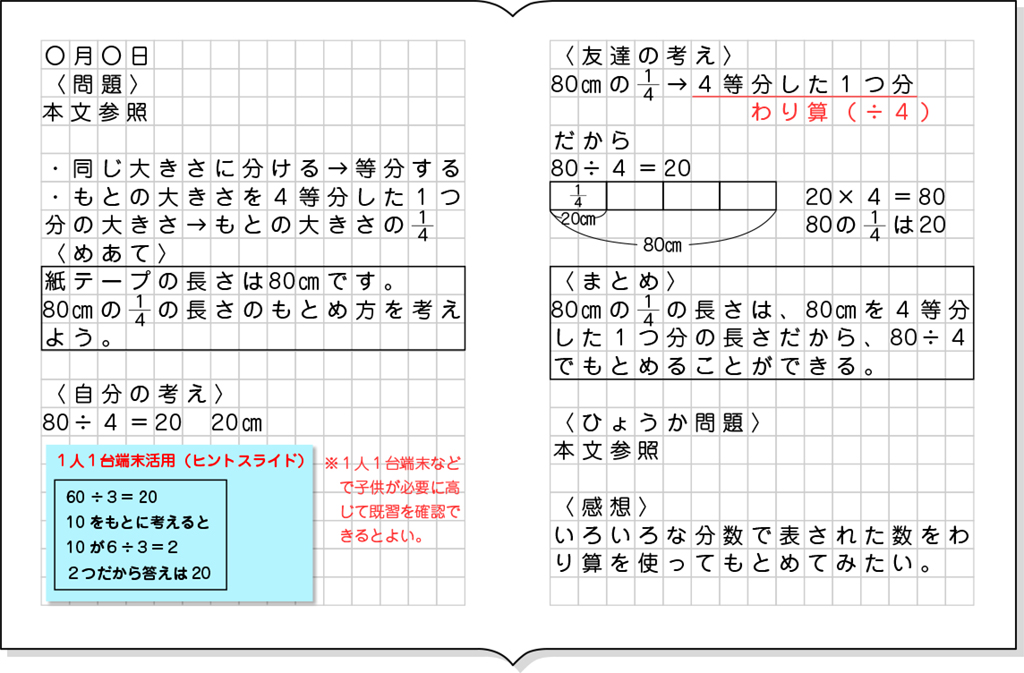
ノート例
B 素朴に解いている子

A つまずいている子(つまずいた際のヒントカードなどの支援付き)
全体発表とそれぞれの考えの関連付け
80㎝の[MATH]\(\frac{1}{4}\)[/MATH]の長さをどのように求めましたか。
イラスト/横井智美

