小６算数「拡大図・縮図」 指導アイデア《対応する辺の長さや角の大きさを基にした拡大図のかき方》

執筆／福岡教育大学附属福岡小学校教諭・西島大祐
監修／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

単元の展開

第１時　対応する辺の長さを簡単な比で表すことで、拡大図と縮図の意味と性質を考える。
▼
第２時　拡大図と縮図について、対応する辺の比から、何倍の図であるかを考える。
▼
第３時　方眼紙を利用した拡大図と縮図のかき方を考え、実際にかく。
▼
第４時（本時）対応する辺の長さの比や対応する角の大きさを基に、縮図のかき方を考える。
▼
第５時　対応する辺の長さの比や対応する角の大きさを基に、縮図のかき方を考える。
▼
第６時　１つの頂点を中心とした拡大図・縮図のかき方を考える。
▼
第７時　任意の点を中心にした拡大図・縮図のかき方を考える。
▼
第８時　縮尺の意味と表し方について考える。
▼
第９時　身の回りの長さの測定に縮図の考えを活用し、実際の長さを求める。
▼
第10時　学習内容の習熟・定着を図る。

本時のねらい

２つの図形の辺の長さや角の大きさの関係に着目し、拡大図をかく方法を考え、説明することができる。

評価規準

三角形の拡大図をかくのに必要な３つの要素を判断し、かくことができる。（思考力・判断力・表現力等）

本時の展開

三角形ＡＢＣを２倍に拡大した三角形ＤＥＦのかき方を考えましょう。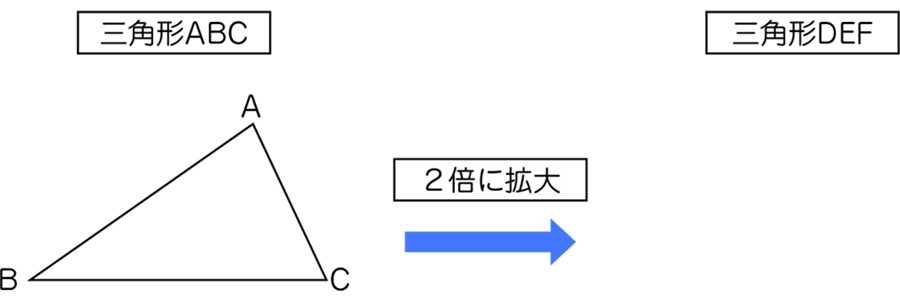

※ＢＣ＝６㎝、角Ｂの大きさが35°、角Ｃの大きさが65°の三角形を使っています。このとき、角Ａの大きさは80°、ＡＢの長さは約5.5㎝、ＣＡの長さは約3.5㎝です。 はじめに、三角形ＡＢＣを提示し、この２倍の拡大図である三角形ＤＥＦをかくには、どの辺の長さや角の大きさが分かればよいかを話し合う活動を行います。次に、相似の性質（対応する辺の長さの比がすべて一定であること、対応する角の大きさがすべて等しいこと）をふり返り、解決の見通しにつなげるようにしていきます。

※見通しの段階では「すべての辺の長さや角の大きさを測る必要があるか」と問い返し、五年生での合同な図形のかき方との共通点につなげていくようにします。

辺の長さの比や角の大きさに目を付けて、拡大図のかき方を考えよう。

自力解決の様子

A　つまずいている子

拡大図を正しくかくことができない。

Ｂ　素朴に解いている子

辺の長さや角の大きさをすべて使って拡大図をかくなど、作図に必要な３つの構成要素を適切に判断できていないが、拡大図はかくことができている。

Ｃ　ねらい通り解いている子

３つの辺の長さをそれぞれ２倍するかき方、２つの辺の長さをそれぞれ２倍にして、その間の角の大きさを使ってかくかき方、１つの辺の長さを２倍にした長さとその両端の２つの角の大きさを使ってかくかき方で、拡大図をかくことができている。

学び合いの計画

Ａの子供については、２倍の拡大図の辺の長さや角の大きさが捉えられていないことや、それらは捉えられていてもどこからかき始めればよいかが分からず、作図にとりかかれないことが予想されます。

三角形ＤＥＦの辺の長さや角の大きさを一緒に確認するとともに、まずは底辺である辺ＥＦをかき、その後、どの辺の長さや角をかくか考えさせましょう。

Ｂの子供に対しては、正しくかけていることを賞賛したうえで、辺の長さや角の大きさを最低何か所使えばよいか、考えるよう促しましょう。

Ｃの子供に対しても、一通りの方法で活動を終えている場合は、ほかの方法を考えるよう促しましょう。

１人１台端末の活用により、ほかの子供の解法を見ることで、ＡやＢの子供は正しい作図やよりよい作図の方法を知ることにつながるかもしれません。Ｃの子供もほかの方法があることを知り、自分でも作図してみることにつながるかもしれません。

ただし、ほかの子供の解法を見て真似をするのではなく、第５学年の合同な図形の作図の方法をふり返ることで、作図の方法を考えることができれば、より望ましいでしょう。

ノート例

イラスト／横井智美、やひろきよみ