小4算数「直方体と立方体」指導アイデア（7/9時）《垂直なのはどの面ですか？》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2022.12.15

単元の展開

（１）直方体と立方体
第１時　身の回りの箱の形に関心をもち、既習の平面図形を基に直方体や立方体、立体の意味を理解する。
▼
第２時　構成要素に着目して、直方体や立方体の特徴について考える。
▼
第３・４時　辺の長さや面のつながりなどに着目して、直方体と立方体の展開図をかく。
▼
（２）面や辺の垂直・平行
第５時　直方体の面と面の垂直・平行の関係を理解する。
▼
第６時　直方体の面と辺の垂直・平行の関係や、辺と辺の垂直・平行の関係について考える。
▼
第７時（本時）直方体の展開図による構成要素の位置関係についての考察を深める。
▼
第８時　直方体、立方体の見取図をかく。
▼
（３）位置の表し方
第９時　平面上や空間にある点の位置の表し方について理解する。

１人１台端末活用ポイント

第１時では、仲間分けに使用する身の回りの箱の写真を端末にアップします。写真を移動させることで仲間分けをしたり、そのように仲間分けをした理由をタッチペンで書き込んだりすることで、構成要素に着目しやすくなります。

第３・４時では、直方体や立方体を切り開き、平面になっていく様子が分かるデジタルコンテンツを各端末で活用。繰り返し確認することができ、一人一人に合ったペースで確実に理解できます。また、切り開く辺によって異なる展開図になることも視覚的によく分かります。

第６時では、直方体と立方体の見取り図を端末にアップします。面と面の位置関係を、垂直や平行に分けて色を塗ることで、面の位置関係に着目し、垂直と平行の関係を視覚的に捉えることができます。面と辺、辺と辺の位置関係を調べる際にも、同様に活用できます。

本時のねらい（立体の模型を用いて、直方体と立方体の面と面、辺と面、辺と辺の位置関係について学習した後）

見いだした直方体の特徴や構成要素の位置関係などを根拠にして、展開図のなかのある面と垂直な位置関係にある面について筋道立てて考える。

評価規準

見いだした直方体の性質や構成要素の位置関係などを根拠にして、展開図のそれぞれの面のつながりや位置関係について考え、表現している。（思考･判断･表現）

本時の展開

「面㋓」と垂直なのは、どの面ですか。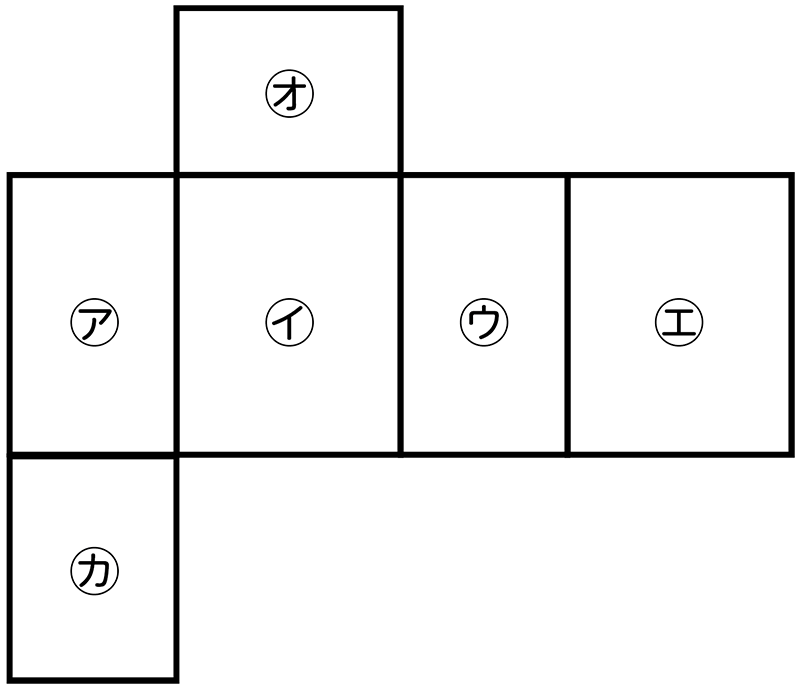

この展開図を組み立てると、どんな形ができると思いますか。

直方体ができます。どの面の形も長方形だからです。

面が６つあるし、組み立てたときに重なってしまう面がなさそうだから、直方体がつくれます。

これまで、直方体の立体の模型や図を見ながら、面や辺の垂直・平行の関係を見付けてきましたね。今日は、この展開図を見ながら、垂直や平行の関係を考えていきましょう。

展開図から垂直や平行を考えるのは難しそうだな。

でも、直方体の特徴は、立体でも展開図でも同じはずだから、今までに勉強してきた直方体の特徴を基に考えたらいいと思うよ。

展開図のなかから、垂直の関係になる面の見付け方を考えよう。

見通し

展開図を頭のなかで組み立て、直方体の特徴に当てはめて考えよう。（方法の見通し）

垂直な面は４つあるはずよ。（結果の見通し）

自力解決の様子

A つまずいている子

面㋒だけが垂直な面
●面㋓と接している面だけが垂直の関係だと考えている。

Ｂ素朴に解いている子

面㋐､面㋒､面㋔､面㋕が垂直な面
●展開図を立体に組み立てた様子をイメージして考えている。

Ｃねらい通り解いている子

面㋐､面㋒､面㋔､面㋕が垂直な面
●直方体の特徴に基づいて考えている。

直方体には６つの面がある。
１つの面に対して、平行な関係の面は１つだけで、ほかの４つの面は垂直の関係にある。
１つの面に垂直なのは、隣り合う４つの面である。
ある面と隣り合う面は、同じ辺でくっついている。
同じ辺でくっついているということは、展開図に表したときに辺と辺が重なるということ。

この５つのことがらを基にして、面㋓と垂直の関係にある面を見いだしている。さらに、ほかの展開図でも使える考えなのか確かめたいと考えている。

学び合いの計画

本時は、展開図を見てそれぞれの面の位置関係を考える問題場面です。しかしながら、空間の認知には個人差が大きいので、子供たちの自力解決での様子を捉え、必要な子供には、色分けした直方体の立体模型を持たせるなどの手立てを講じるようにしておくとよいでしょう。

本時の学習を進めていくには、展開図上の重なる辺を明らかにすることがポイントです。

直方体の１つの面に対して垂直な面は４つある。
直方体のある１つの面に垂直な面は、その面に隣り合う４つの面である。
隣り合う面と面は、同じ辺でくっついている。
同じ辺でくっついているということは、展開図に表したときに辺が重なるということ。
同じ辺でくっついていても、展開図に表したときに離れて見える辺もある。

などを、言葉を用いて、考えを見える化していく過程をていねいに取り扱っていきましょう。

その際、言葉だけでなく、実際に直方体の立体模型を使って確かめることが大切です。一つ一つの具体的な操作によって確かめることで、立体図形と立体図形の平面上での構成のしかたをしっかり結び付け、実感をともなって理解することができるようになります。

ノート例

全体発表とそれぞれの考えの関連付け

面㋓と垂直の関係になるのは、どの面でしたか。

面㋐、面㋒、面㋔、面㋕が垂直になります。

どのようにして、垂直になる面を見付けたのですか。

私は、この展開図を直方体に組み立てていく様子を頭のなかでイメージしながら考えました。まず、面㋑を底の面にして、面㋔を立てます。次に、面㋐と面㋒を立てます。そうすると、面㋕が回り込むように立ちます。最後に、面㋓が上の面になります。

面㋓に垂直な面を見付けるのだから、面㋓を底の面にして、頭のなかで組み立てることができたら簡単だと思って頭のなかで組み立ててみたけど、途中で分からなくなってしまいました。

頭のなかで組み立てるのは難しいなあ。

■筋道立てて考える

僕は、直方体の特徴を基に考えました。直方体の１つの面に対して、垂直な面は４つあるから、答えになる面は４つあることが分かります。

この垂直になる４つの面は、１つの面と隣り合っています。

隣り合う面と面は、同じ辺でくっついています。

辺がくっついているということは、展開図にしたときに、辺が重なるということです。

えっ？　でも、それだったら、面㋓と垂直なのは、面㋒だけということになるのではないの？　面㋓の辺と重なっているのは、面㋒の辺だけになるよ。

確かに、この展開図をぱっと見ると、面㋓と面㋒の辺だけがくっついて見えます。だけど、この（下の図の）ように、面㋓の残りの３つの辺は、直方体に組み立てると、面㋐、面㋔、面㋕の辺と重なるんです。

確かに！　ぱっと見たら重なっていなくても、実際は重なるね。

展開図をぱっと見ただけで判断しないで、重なる辺はどこになるか考えると、１つの面と隣り合う面がどれなのか分かるんだね。

垂直の関係になる面は、「垂直な面は４つ」→「１つの面と隣り合う」→「辺どうしがくっついてる」→「辺は重なる」というように、順番に考えていくと正しく見付けることができるね。

■見付け出したことから、さらに考えを深める

みんなの考えを聞いていて気付いたのだけど、全部で６つある面のなかで垂直な面が４つということは、残りの２つの面は、もとにしている面とそれに平行な面ということになるよね。

確かにそう。もとにしている面と垂直な面は４つで、平行な面は１つになるね。

そうか！　分かった！　それなら、平行な面を先に１つ見付ければいいんだ。

そうそう。もとにしている面のほかの５つの面のなかから平行な面さえ見付けられたら、残りの４つの面はどれも垂直な面ということになるよ。

なるほど。垂直な面を見付けるには、まず平行な面を見付けたらよいというわけですね。

平行な位置関係の２つの面は、展開図にしたとき隣り合うことはないよ。それに、もとにしている面と同じ形をしているから見付けやすいよ。

今回の展開図で考えると、面㋓と隣り合っていなくて、同じ形をしている面は、面㋑だね。

面㋓と面㋑が平行なのだから、残りの面㋐、面㋒、面㋔、面㋕が垂直だと分かるね。

面㋓に垂直な面は、面㋐、面㋒、面㋔、面㋕の４つ

展開図のなかから垂直の関係になる面を見付けるには、直方体の特徴を基にして、順序よく考えていくとよい。
・直方体の１つの面に垂直な面の数は、４つある。　　　　
↓
・この４つの面は、直方体の１つの面と隣り合っている。
↓
・隣り合う面と面は、同じ辺でくっついている。
↓
・同じ辺でくっついているということは、展開図にしたときに辺が重なるということ。
　
・直方体のある１つの面に対して、平行な面は１つ、垂直な面は４つある。
・平行な面どうしは、展開図にしたときに隣り合うことがなく、同じ形をしている。
だから、
・まず、直方体の１つの面に対して、平行な面を見付ける。（面㋑）
・すると、残りの４つの面が直方体の１つの面に垂直な面なので、簡単に見付けることができる。

評価問題

面㋔と垂直な面はどれですか。

子供に期待する解答の具体例

面㋔と垂直な面は４つ。
面㋑だけでなく、面㋐や面㋒などとも隣り合う。（辺を共有している。辺が重なる。）

だから、面㋔と垂直な面は、面㋐、面㋑、面㋒、面㋓

本時の評価規準を達成した子供の具体の姿

見いだした直方体の性質や構成要素の位置関係などを根拠にして、展開図のある面と垂直な位置関係にある面を筋道立てて考えている。

感想例

「垂直な面は４つ」→「１つの面と隣り合う」→「辺どうしがくっついている」→「辺は重なる」というように、順番に考えていくと、正しく見付け出していけることがよく分かりました。
ぱっと見ただけで判断しないで、順序よく考えていくことが大切だなと思いました。
展開図を見ながら、面と面の垂直・平行、面と辺の垂直・平行、辺と辺の垂直・平行などを考えるときも、直方体の特徴を基に、順序よく考えていきたいです。
ただ答えを出すだけでなく、答えを見付け出すまでの考え方を話し合って、その答えの意味を考えたことで、深く学ぶことができました。これからも、このような学び方をしていきたいです。

イラスト／横井智美

【関連記事】

1人1台端末時代の｢教科指導のヒントとアイデア｣シリーズはこちら！