小5算数「円と正多角形」指導アイデア《コンパスを使って正六角形をかこう》
執筆/福岡県北九州市立若園小学校教諭・栗原省吾
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 辺や角に着目し、正多角形の定義や性質を理解する。
▼
第2時 正多角形の性質に基づき、円の中心の周りの角を等分して正多角形をかく方法を考える。
▼
第3時(本時)正多角形や円の定義や性質に基づき、円を使って正六角形をかくことができる理由を考え、説明することができる。
▼
第4時 正多角形の性質に基づき、円周と直径の関係について考える。
▼
第5時 円の直径の長さと円周の長さの関係について考える。
▼
第6時 円周率について知り、円周の長さや直径の長さを求める問題を解決する。
▼
第7時 円周の長さと直径の長さの関係を、比例という観点から捉える。
▼
第8時 本単元の学習内容の定着及び円周の長さを活用する問題を解決する。
本時のねらい
正多角形や円の定義や性質に基づき、円周を6等分することで正六角形をかくことができる理由を考え、説明することができる。
評価規準
円周を6等分する方法で正六角形をかくことができ、その方法で正六角形がかける理由を説明することができる。(知識・技能)
本時の展開

ひなたさんは、コンパスを使って、さまざまなもようづくりをしていました。図のように半径7㎝に等しく開いたコンパスで円のまわりを順に区切って印をつけたものを結ぶと、ある図形ができました。どんな図形ができたか、実際にかいて調べてみましょう。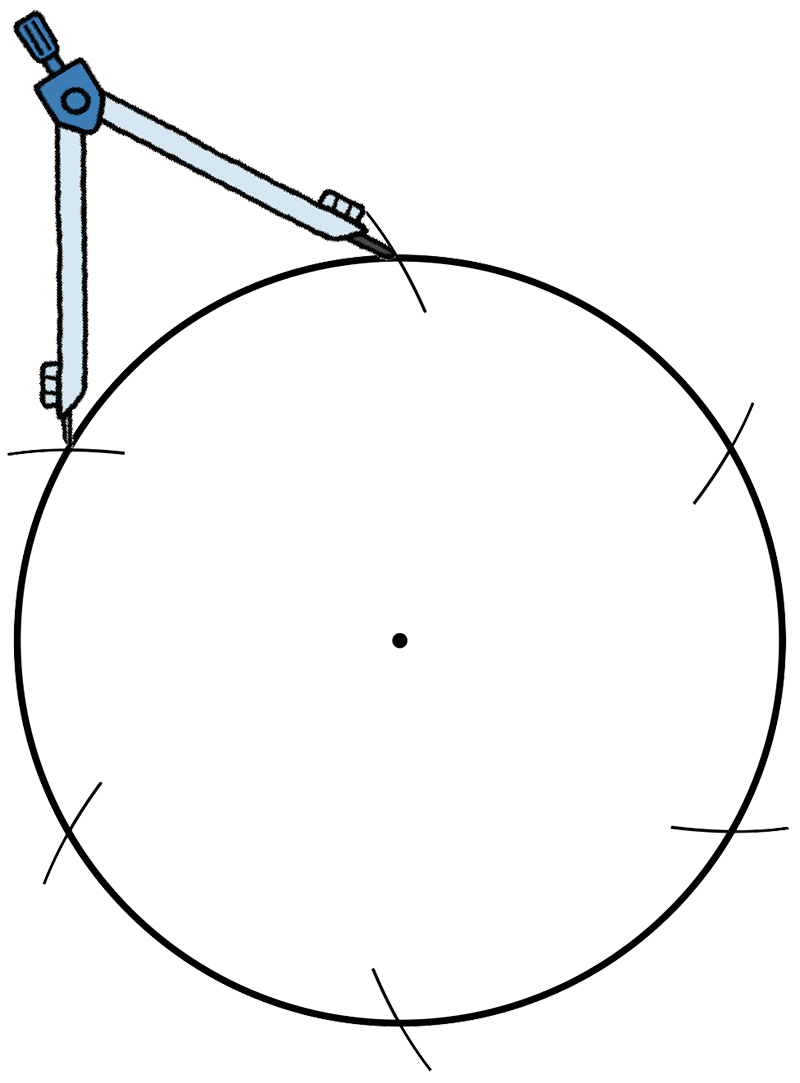
本時では、はじめにコンパスを使って正六角形の作図を行います。
この作図の方法を発見させることが本時の主眼ではないので、六つの印をコンパスで付けていく手順は、黒板で教師が実演したり、デジタル教科書を使ったりしてクラス全体で確認したうえで、子供たちに作図をさせます。
次に、作図した図形が正六角形であることを、第1時で使用した折り紙で作った正六角形(折り紙の辺の長さ14㎝)を使って確かめます。その後、「どうしてコンパスだけで正六角形がかけるのか」という疑問をもたせ、本時のめあてを導きます。
どんな図形ができましたか。
六角形ができました。
この六角形は正六角形だと思います。
なるほど。本当に正六角形がかけたのか、前回折り紙で作った正六角形を重ねて調べてみましょう。
ぴったり重なりました。
この六角形は正六角形です。
皆さんがかいた図形は正六角形ということが分かりましたね。何か不思議に思いませんか。
コンパスでかいていたら、いつの間にか正六角形がかけて不思議です。
前の時間のように、分度器を使っていないのに正六角形がかけたのが不思議です。
これまで正多角形について学習してきたことを基にして、このかき方で正六角形がかける理由について考えていきましょう。

コンパスを使ってかいた図形が、正六角形になるわけを考えよう。
自力解決の様子
A つまずいている子
図はかけるが、これまでの学習に基づいて、理由を説明することができない。または、六つの辺の長さがすべて等しいことだけを定規やコンパスを使って確かめ、説明している。
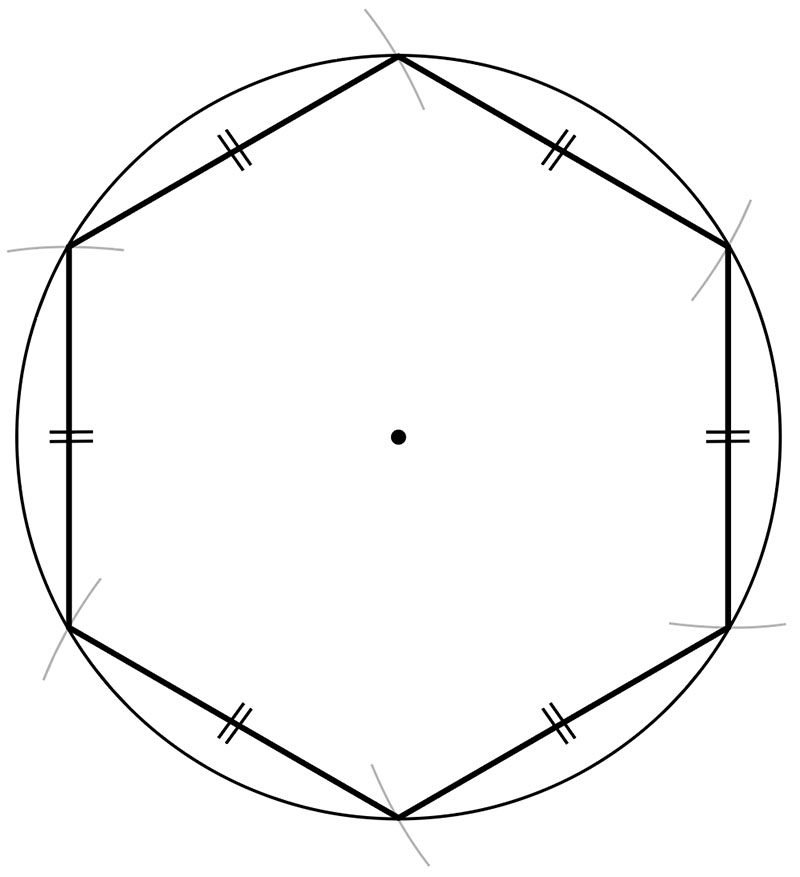
B 素朴に解いている子
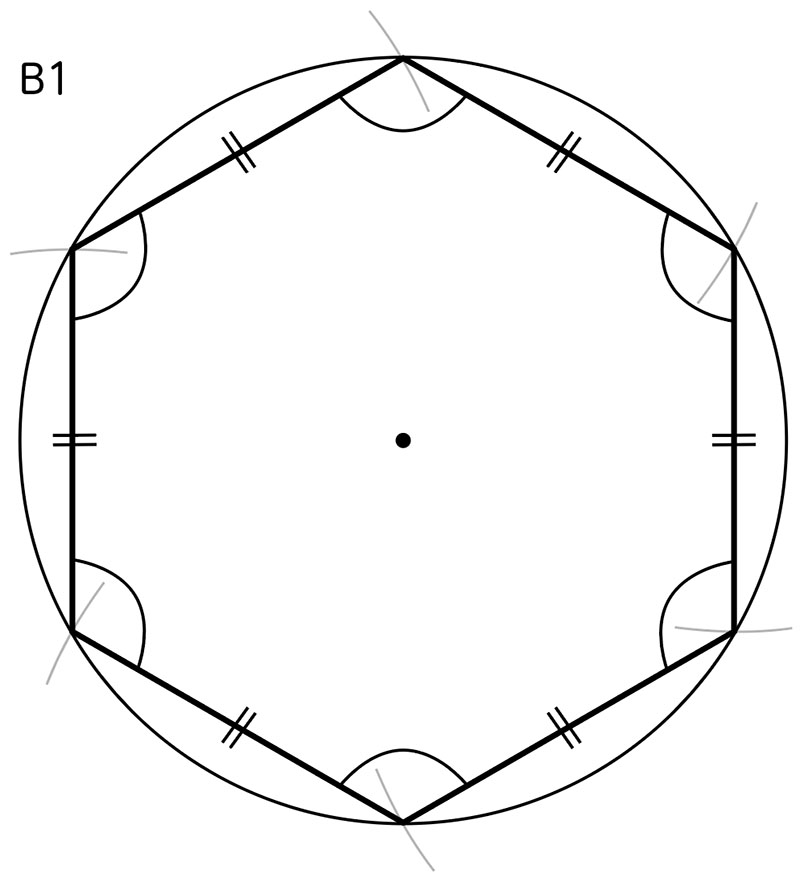
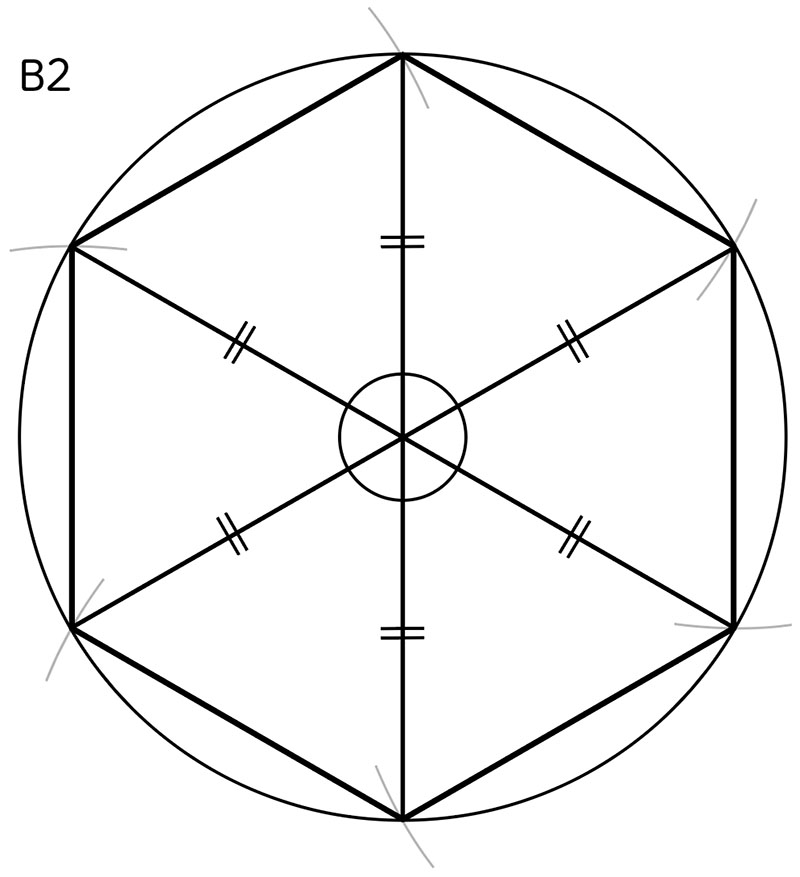
六つの辺の長さがすべて等しいことを定規やコンパスで確かめるとともに、分度器を使って六つの内角の大きさ(B1)、または、中心の角の大きさ(B2)がすべて等しいことを確かめ、説明している。
C ねらい通り解いている子
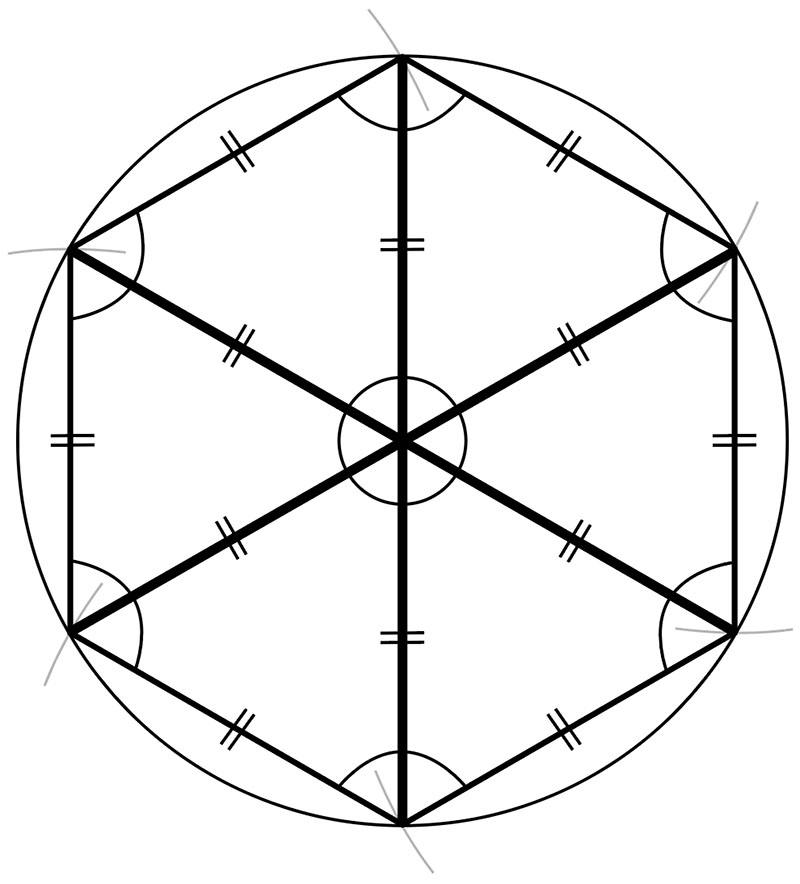
正六角形が六つの合同な正三角形でできていることに基づき、六つの辺の長さや六つの内角(または六つの中心の角)の大きさがすべて等しくなることを説明している。
ノート例
イラスト/横井智美、やひろきよみ

