小3算数「何倍でしょう」指導アイデア《倍の数量の求め方》

執筆/神奈川県横浜市立師岡小学校教諭・横地健一郎
監修/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 比較量の求め方の考察
▼
第2時(本時)倍の求め方の考察
▼
第3時 基準量の求め方の考察
本時のねらい
数量の関係に着目して、倍を求める場合は除法を用いればよいことに気付き、倍を用いた乗法と除法の関係について考えることができる。
評価規準
数量の関係に着目して、倍の求め方を言葉、図、式を用いて説明している。
本時の展開

あずささんのえんぴつは5㎝、ちづるさんのえんぴつは20㎝です。ちづるさんのえんぴつは、あずささんのえんぴつの何倍ですか。
前の時間の学習では、もとにする大きさの何倍に当たる大きさを求める計算について勉強しましたね。
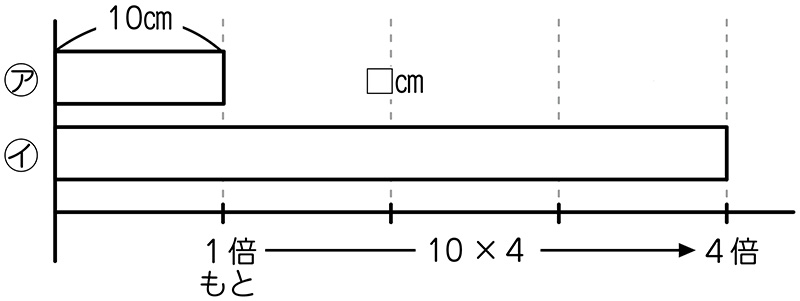
かけ算を使いました。
そうそう。もとが1倍で、もとを4倍すると答えが出ました。
今日のこの問題は、何算になりそうですか。
倍とついているから、かけ算だと思います。
何倍と聞かれているから、わり算になると思います。
どうしてそう考えたのですか。
前は倍に当たる大きさが分からなくて、それを知りたいからかけ算を使ったので、今日は、かけ算ではないと思いました。
今日は、前の時間と□の場所が違います。
ほんとだ。□の位置が違う。倍のところが□だよ。
今、□の位置が違うという話が出ましたが、□の位置はどこになりますか。
図をかいて確かめたい。
では、図をかいて、倍を求める計算は何算になるか、考えていきましょう。どんな図がかけますか。

数量の関係に着目して、倍の求め方を言葉、図、式を用いて説明している。
見通し
図をかいたら何算になるか分かるよ。(方法の見通し)
図で□の場所に気を付けたり、まずはかけ算で考えたりしたいな。(方法の見通し)
□の場所がいくつ分を求めるときと同じになるから、わり算になるね。(結果の見通し)
自力解決の様子
A つまずいている子
図に数量の関係を表したり、図から数量の関係を読みとって式に表したりすることができていない。
B 素朴に解いている子
図から読みとった数量の関係から、わり算になるように式を考えている。
C ねらい通り解いている子
数量の関係を的確に図に表し、図からわり算になる根拠を捉えようとしている。
学び合いの計画
倍については、第2学年において「〇のいくつ分」のことを「〇の何倍」ということや、何倍かに当たる大きさを求めるときは乗法の式に表すことを、テープの長さなどを題材として学習してきています。
イラスト/横井智美

