小6算数「円の面積」指導アイデア
執筆／東京都公立小学校教諭・越後真紀
編集委員／文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
（本時の位置 1／7 単元の導入）
ねらい
円のおよその面積を、既習の考えを使って面積を求めることができる。
評価規準
既習の考えを使って円のおよその面積の求め方を考えることができる。
問題
今まで学習してきた図形の中で面積が求められない形はあるかな?
今まで6年間を振り返ってどんな図形について学習してきたかな?
三角形、四角形、五角形、六角形、円……。
二等辺三角形、直角三角形、正三角形、長方形、正方形、平行四辺形、台形、ひし形…。
それらの形についてどんな学習をしてきたかな?
辺の長さ、角の大きさ、平行や垂直、面積……。
円の面積だけまだ求められません。
では、今日は円の面積の求め方を考えよう。
最高学年ということで、今まで学習してきた図形とそれぞれの図形の何について学習してきたか、既習（周りの長さ、内角の和、面積）をまとめる活動を行います。図形に対する総復習になると同時に、円の面積だけが未習であることをはっきりさせます。さらに「円の面積の求め方を考えたい」という思いが児童の中に自然とわくと思われます。また、既習をまとめる活動を通して、見通しをもつ際、既習に立ちもどりやすくなるメリットもあります。
本時の学習のねらい
半径10㎝の円の面積の求め方を考えよう。
面積は、1㎠の単位正方形がいくつあるかで表すことができることや、1㎠に満たない半端な面積は、2つで1㎠とすることを共通理解させます。
円に内接する正方形の面積より大きく、円に外接する正方形の面積より小さいことから、半径10㎝の円の場合200㎠＜円の面積＜400㎠となります。円に外接する正方形は直径×直径＝半径×2×半径×2＝半径×半径×4で、円に内接する正方形（下図）は、半径×半径×2であることを図と関連付けながら児童と共に確認します。そこから、円の面積は半径×半径の2倍より大きく、半径×半径の4倍より小さいので、円の面積は半径×半径の3倍位ではないかという予想をもたせます。
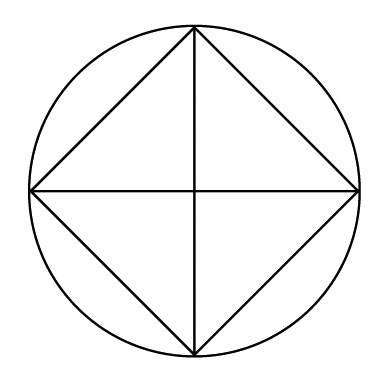
円の面積が本当に半径×半径の3倍くらいなのか、半径10㎝の円の面積を求めてみよう。
見通し
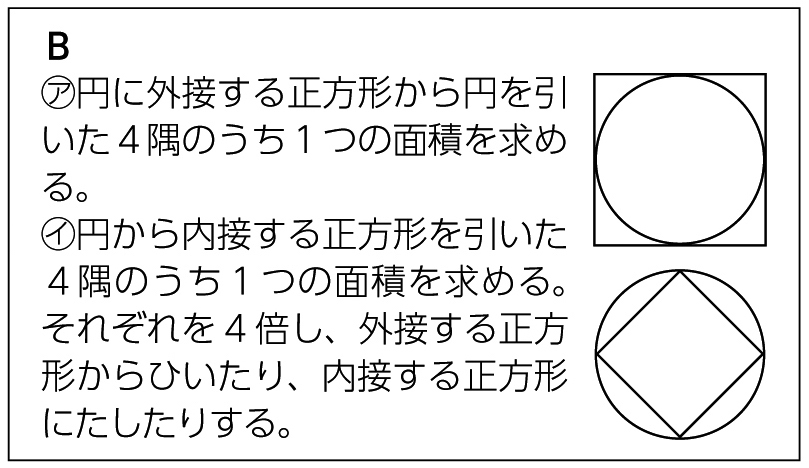
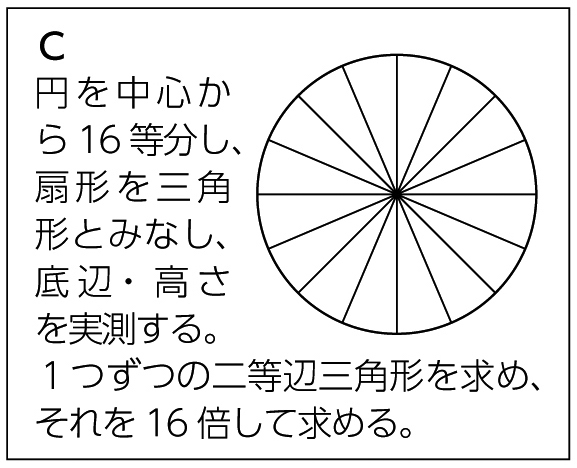
自力解決の様子
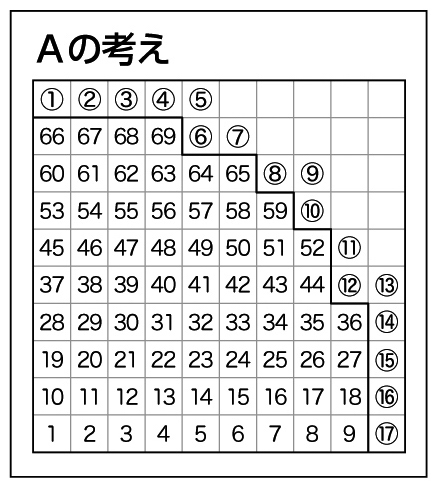
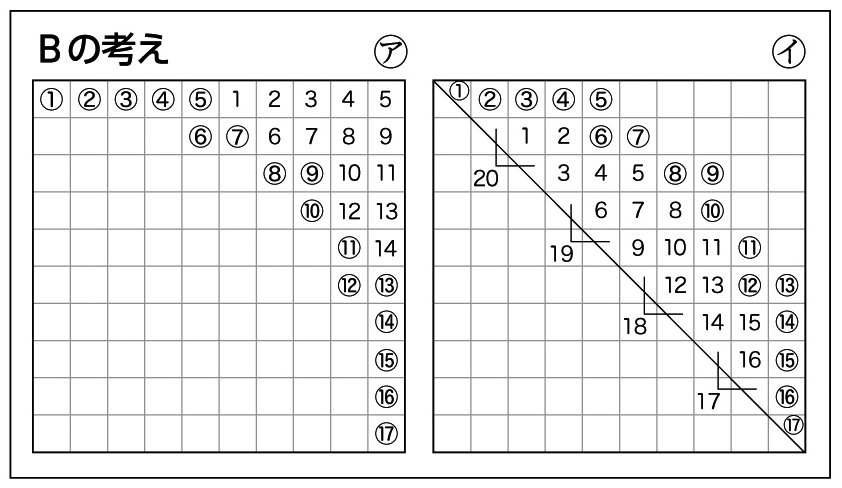
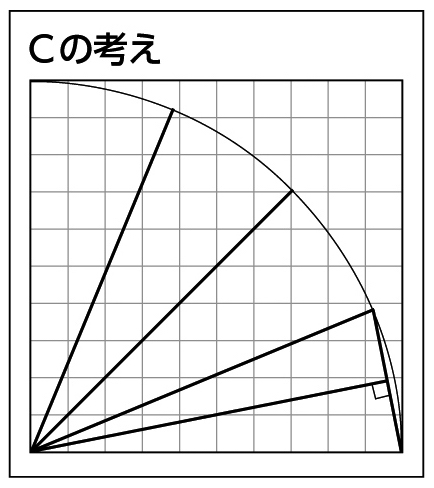
学び合いの計画
AやBは、1㎠に満たないものをすべて半端として全部たして÷2をすることで、誤差が生じることを押さえます。円の面積は、およそ310～316㎠になります。
イラスト／横井智美
『教育技術 小五小六』 2020年7/8月号より
