小5算数「直方体と立方体の体積」指導アイデア
執筆／新潟県公立小学校教諭・内山大樹
編集委員／文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋 哲
目次
本時のねらいと評価規準
（本時の位置 １/10時）
ねらい
箱を直接重ねたり、任意単位で敷き詰めたりする活動を通して、立体の大きさ比べでは任意単位のいくつ分を数えればよいことに気付く。
評価規準
任意単位で敷き詰める大きさ比べの方法に気付いている。
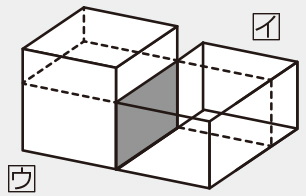
問題場面
スーパーマーケットで箱にキャラメルを詰め放題できるイベントをやっていました。次の３種類の箱の展開図のうち、どれか一つを組み立てて、詰めるというものでした。
実物よりも10倍に拡大した３種類の展開図を提示して、問題場面のイメージをもたせます。また、最初に辺の長さを示さないことで、辺の長さに着目させ、実物で比べてみたいという意欲を引き出します。
みんななら、どの箱を選びますか。
やっぱり一番大きな箱がいいな。
この中ならイかウが大きそうだ。
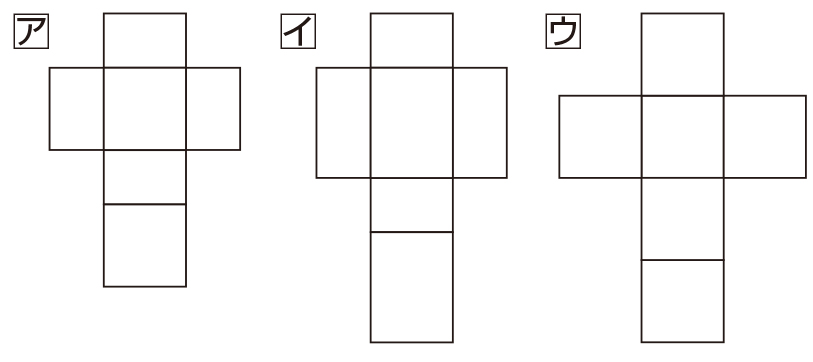
それぞれの箱の辺の長さは何㎝ですか。
アは2㎝・3㎝・3㎝、イは2㎝・3㎝・4㎝、ウは3㎝・3㎝・3㎝です。
辺の長さを足してみると、アは8㎝、イは9㎝、ウは9㎝だから、大きな箱はイとウだ。アは一番小さい箱だと思う。
ぼくは実際の箱を重ねて比べてみたいな。イとウのどちらが大きいのかな。
キャラメルの大きさも知りたいな。
ここに３つの箱と、キャラメル（１㎤の立方体模型）と同じ大きさのものを用意しました。どの箱が一番大きいと言えるのか、確かめてみましょう。
本時の学習のねらい
箱の大きさはどのようにすると比べることができるだろうか。
見通し
３つの辺の長さを足すと分かるよ。
直接重ねてみれば分かるよ。
キャラメルを、きちんと箱に並べると分かるよ。
自力解決の様子
A つまずいている子
「辺の長さを足すと、ア：8㎝、イ：9㎝、ウ：9㎝。イとウ」
・辺の長さから考えている子
Ｂ 素朴に解いている子
ア、イ、ウを重ね、アが小さい。イかウかは分からない。
・直接比較で考えている子
Ｃ ねらいどおり解いている子
「キャラメルの数を数えると、ウが一番多いからウ」
・任意単位で考えている子
学び合いの計画
立体の大きさを児童はどのように捉えているでしょうか。
イラスト／横井智美
『教育技術 小五小六』 2021年4/5月号より
