小6算数「算数のまとめ」指導アイデア《他の国の算数について調べたり、問題に取り組んだりする》

執筆/富山県射水市立大門小学校教諭・前田正秀
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、富山大学附属小学校教諭・羽柴直子
目次
年間指導計画
・対称な図形
・文字を使った式
・場合の数
・分数×÷整数
・円の面積
・分数×分数
・分数÷分数
・角柱と円柱の体積
・資料の調べ方
・小数と分数の計算
・比と比の利用
・拡大図・縮図
・比例と反比例
・およその面積と体積
・算数のまとめ
単元の展開(各時の主な学習活動内容)
第1時 中学校の数学の問題(0より小さい数)に取り組む。
第2時 中学校の数学の問題(図形の性質を利用した作図など)に取り組む。
第3時(本時)他の国の算数について調べたり、問題に取り組んだりする。
第4時 和算について調べたり、和算の問題に取り組んだりする。
第5時 算数のクイズ(仕事算)に取り組む。
第6時 算数のクイズ(面積図など)に取り組む。
第7時 算数のパズル(魔方陣など)に取り組む。
本時のねらい
他の国の算数についての興味・関心を広げる。
評価規準
自分と異なる計算のやり方に興味をもち、他の国の算数を試そうとしている。
本時の教材のポイント
これまで学習してきた「かけ算の筆算」の学習の発展として、世界のいろいろなかけ算の方法を紹介します。ここでは、様々な方法を単に知識として知るだけでなく、今、自分が使っている筆算との「違うところ」や「共通するところ」に目を向けていくことが大切です。それぞれの方法を比較する中で、子供たちは、どの方法も「位ごとに分けて考えて、後から足す」という原理は共通していることに気づくことでしょう。こうした活動を通して、かけ算の理解を深めると共に、算数の面白さを感じてほしいと思います。
本時の展開
まずは、線を引くだけで答えが求められる計算方法を紹介します。諸説ありますが、古代インドで縄と石を使って行った計算方式とも言われています。
今日は、線を引くだけで答えが求められる魔法のかけ算の計算方法を紹介します。その方法は、九九を覚えていなくても計算できるんですよ。今から12×23の計算をします。先生が何をしているか見ていてください。
※黒板に線を1本引く。
直線をひきました。
直線を1本、斜めに引きました。
では、続けます。何をしているか見ていてください。
※黒板に線を2本引く。
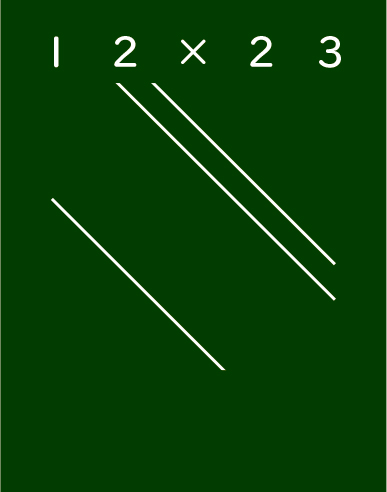
直線を2本、斜めに引きました。
では、続けます。何をしているか見ていてくださいね。
※黒板に線を2本引く。
直線を2本、さっきとは違う向きで引きました。
では、次はどうすると思いますか。
線を3本、右上から左下の向きで引くと思います。
23の3だから、3本引くと思います。
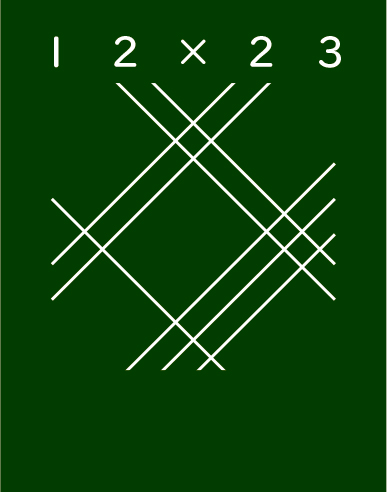
では、続けます。今度は何をするでしょう。
※交点を色チョークで囲み、2、7、6と書く。
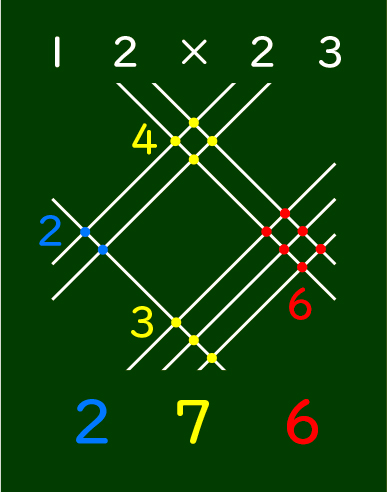
12×23の答えは、276です。
すごい!
本当に答えが合っているかどうか、疑う子もいるでしょう。そういう思考は大切です。実際に、筆算をして確かめてみるとよいでしょう。答えが合っていることが分かると、子供からは驚きの声があがります。さらに、他の数でもできるかどうか、試してみることも必要です。自由に数を当てはめて、試させてみるとよいでしょう。最初は、この方法を「すごい」「最高」と言っていっていた子供たちも試しているうちに、「あれ、これだと……」とざわめき始めます。この方法だと、98×97といったように各位の数が大きくなると線が多過ぎてノートがぐちゃぐちゃになってしまうという欠点に気づくのです。現在の日本で学習している筆算方法は、数が大きくなってもできます。他の方法と比較することで、そうしたよさを改めて知ることができるのです。

線で求める方法と今の日本の筆算を比べて「ちがい」や「同じ」を見付けよう。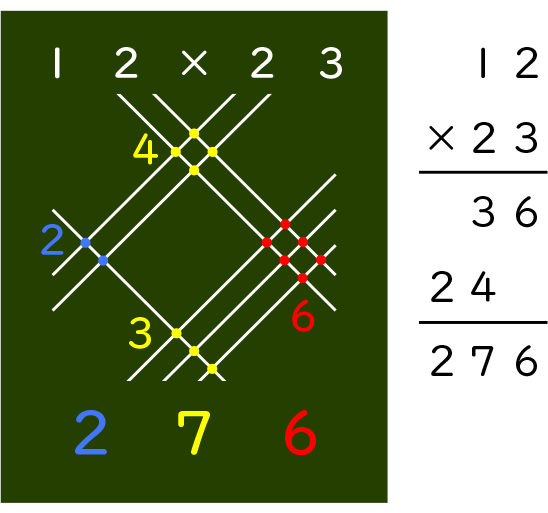

いろいろな計算方法を比べよう。
見通し
面白い計算方法に出合ったとき、子供たちは、今の計算方法と比較しながら、その特徴を捉えます。比較する際、着目しやすいのが「違い」です。「線で求める方法だとかけ算を覚えてなくても答えが求められる。今の筆算だと数が大きくなっても答えが求められる」。そういった「違い」に、まず目が向きます。次に、「共通するところ」を考えさせます。子供たちには「どちらの計算にも共通するところはないですか」と投げかけます。共通点を見付けるのが難しい子供には、「同じ数がありませんか」とヒントをあげると、考えやすくなります。
・違いがないか、比べよう。
・同じ数がないか、比べてみよう。
自力解決の様子
A つまずいている子
・答えが同じことには気づいているが、部分積には着目していない。
B 素朴に解いている子
・どちらにも、部分積の2、3、4、6が共通してあることに気づいている。
C ねらい通り解いている子
・どちらも、位ごとにかけ算していて、部分積の2、3、4、6が共通していることに気づいている。
全体発表とそれぞれの考えの関連付け
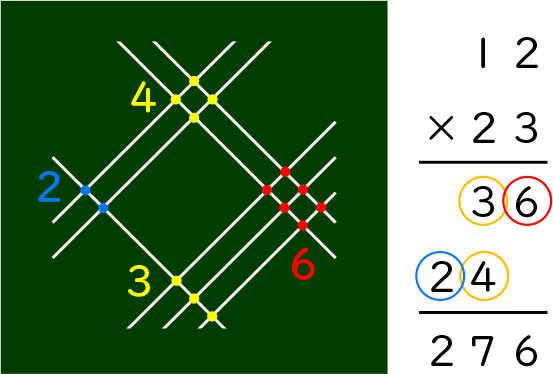
どちらの計算方法にも、共通するところはありませんか。
筆算に6、3、4、2という数が出てくるけれど、線で求める方法にも6、3、4、2があります。
どちらも、3と4を足しています。
どちらも、1の位に2、十の位に3と4、百の位に2と、位ごとに並んでいます。
位ごとに計算しているところが共通しています。
線で求める方法とみんなが使っている筆算は、とても似ているのですね。
これから、線で求める方法も使っていきたいです。
でも、98×97のような計算では、線をたくさん引くことになるから、見にくくなると思います。
確かにそうですね。線を9本、8本、9本、7本引いて、さらに、交わったところを数えるのだから、正確な答えを出すのは難しそうです。
今、私たちが使っている筆算は、それぞれの位の数字が大きくても小さくても、見にくくなることはありません。
筆算のよさがよく分かりました。
まとめ
どちらの計算方法も、位ごとに分けて計算して、後から足している。
ポイント&アドバイス
筆算の特徴は、筆算だけを見ていても気づかないものです。他の方法と比べてみることで、初めて筆算の特徴が見えてくるのです。本授業をするにあたっては、面白い計算方法を紹介するだけでなく、筆算と比べてみることが大切です。
教材研究
位ごとに分けて計算して、後から足す。これは、計算の基本となる考えです。時間が許せば、他にもいくつか計算方法を紹介すると、その理解がより深まります。
①格子算
構成/桧貝卓哉 イラスト/横井智美・やひろきよみ 図版作成/永井俊彦

