小５算数「面積」指導アイデア《高さが三角形の外にある場合の三角形の面積の求め方》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.01.17

単元の展開

第１時　平行四辺形の面積の求め方を考え、説明することができる。
▼
第２時　平行四辺形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第３時　高さが平行四辺形の外にある場合でも、平行四辺形の面積の公式を適用できることを理解する。
▼
第４時　三角形の面積の求め方を考え、説明することができる。
▼
第５時　三角形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第６時（本時）高さが三角形の外にある場合でも、三角形の面積の公式を適用できることを理解する。
▼
第７時　台形の面積の求め方を考え、説明することができる。
▼
第８時　台形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第９時　ひし形の面積の求め方を考え、説明することができる。また、ひし形の面積の公式をつくり出し、それを適用して面積を求めることができる。
▼
第10時　学習の定着を確認する。

本時のねらい

三角形の面積の公式が使える範囲を、高さが三角形の内にある場合から外にある場合へと広げて考える。
※高さが外にある場合とは、頂点から下ろした垂線の交点が底辺上にない場合のこと

評価規準

三角形の底辺と高さの関係に着目して、高さが三角形の外にある場合であっても三角形の面積の公式を用いることができることについて考えている。（思考・判断・表現）

本時の展開

次の三角形の面積を求めましょう。

※方眼の目盛りは１㎝

今日も三角形の面積を求めましょう。三角形の面積を求める公式を確認しておきましょう。

　三角形の面積は、底辺×高さ÷２で求められました。

そうでしたね。では、今回の三角形の面積は求められそうですか。

公式を使えば簡単に求められそうだけど。

そうすると、底辺は辺ＢＣになるから６㎝だね。

あとは高さだね。あれ？高さがうまく求められないよ。

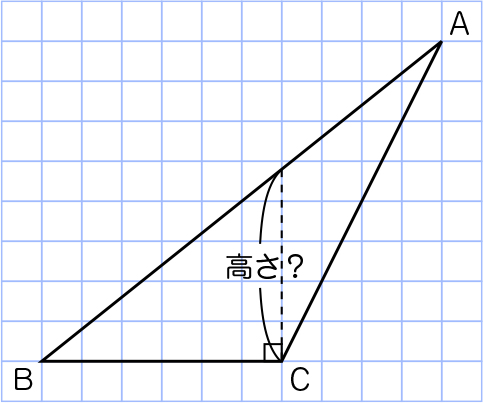
それだと、点Ａを通っていないから、高さとは言えないよ。でも、点Ｃから点Ａに直線を引くと垂直ではなくなってしまうね。

みなさん、悩んでいるようですね。これまでの三角形とどこが違っているのか比べてみましょう。

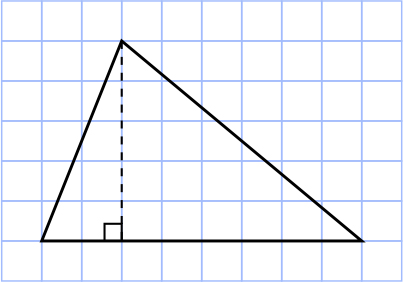
今までの三角形は、高さが図形の中にあったんだ！　今日の三角形は高さが中にないから困っていたんだね。

三角形の中に高さがないときでも、三角形の面積を求める公式は使えるのかな。

これまで習ったことをうまく使って求められないかな。

高さが図形の内にないときの、三角形の面積の求め方を考えよう。

見通し

三角形の内に高さがない場合でも、三角形の面積の求め方はあるはずだ。（結果の見通し）

高さを図の中につくるように、三角形を２つ組み合わせてみよう。（方法の見通し）

頂点Ａから垂線を引いて大きい三角形をつくり、小さい三角形を引くと、三角形ＡＢＣの面積が求められそうだな。（方法の見通し）

平行線を利用して頂点Ａの位置を動かすようにして考えると、高さが図の中になくても三角形の面積を求める公式が使えることが分かった。（方法の見通し）

自力解決の様子

A　つまずいている子
・同じ三角形を２つ組み合わせて平行四辺形をつくり、平行四辺形の公式を基に考えようとしている。
・図形の外にある高さについて、中にある高さと同等であると捉えていない。

Ｂ　素朴に解いている子
・点Ａから辺ＢＣを延長した直線に垂線を引いて点Ｄをつくり、｢三角形ＡＢＤ－三角形ＡＣＤ」を考えて、三角形ＡＢＣの面積を求めている。
・図形の外にある高さを中にある高さと同等であると捉え、三角形の面積を求める公式を使って求めようとしている。

Ｃ　ねらい通り解いている子
・平行な直線の幅はどこも等しいことに着目し、三角形の高さは図形の外にある場合と中にある場合を同等と捉え、高さを図形の外にとっても、公式を使って面積を求められることを理解している。

学び合いの計画

本時は、前時で学習した三角形の「高さ」について、図形の中にあるはずの高さから、図形の外にも高さがあるという見方を広げる場面です。

つまり、三角形の高さを「底辺を伸ばした直線と、底辺と向かい合った頂点を通り、底辺に平行な直線の幅」と捉えることがポイントとなります。

高さが図形の外にあるという捉え方は、前々時に平行四辺形の高さについて考える場面でも行っているため、平行四辺形の高さについてふり返り、学び直すこともできます。

本時では、２つの同じ三角形を組み合わせて平行四辺形をつくり、図形の中に高さをつくろうとする考えに留まらず、平行線の性質に着目し、高さを表す垂線が三角形の高さになる（高さが中にあっても外にあってもよい）ことにまで気付かせることが大切です。

そのため、子供の話合いの場では、図形を示しながら説明させていきます。

その話合いを通して、平行四辺形をつくり、三角形の面積を求めた子供が、「面積を求めるために使った高さは、図形の外にある高さと同じである」ことに気付くよう、子供どうしが積極的に関われるようにします。教師はファシリテーターの立場で臨むとよいでしょう。

ノート例

Ａ　つまずいている子

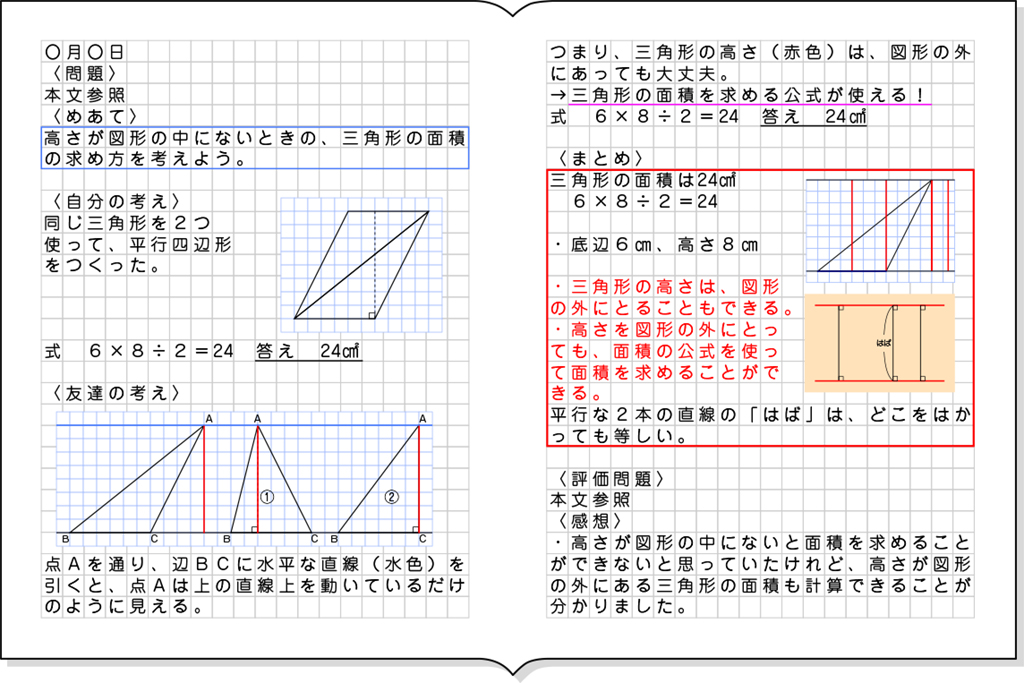
Ｂ　素朴に解いている子

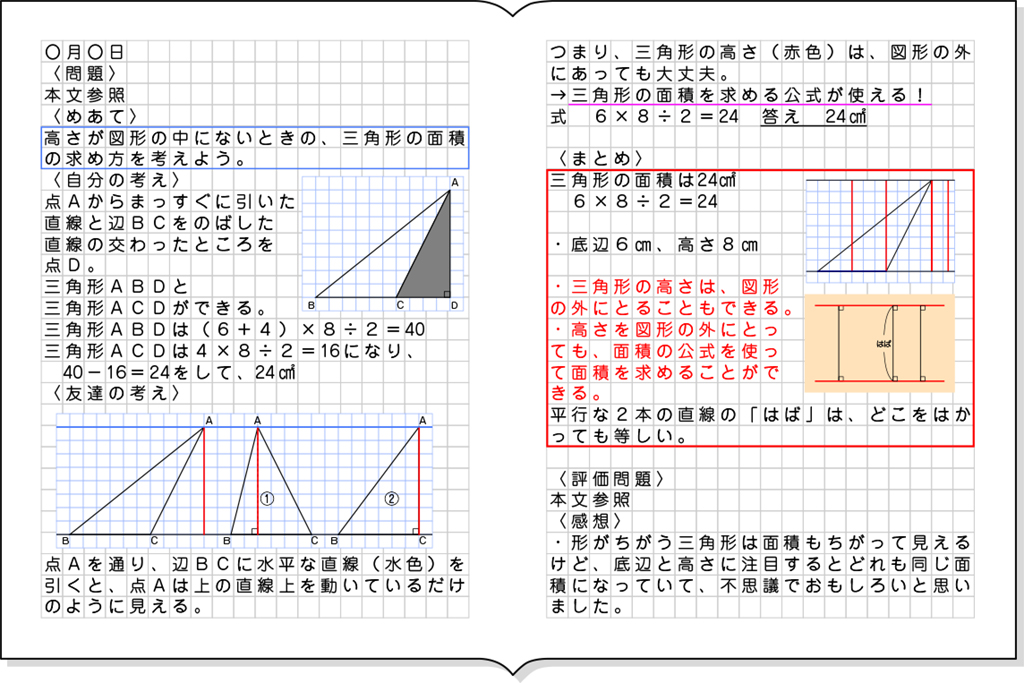
全体発表とそれぞれの考えの関連付け

三角形の高さが図形の中にないときの、三角形の面積の求め方は分かりましたか。

僕は、同じ三角形を２つ使って、平行四辺形をつくりました。こうやって考えると、平行四辺形の公式を使って求められるし、図形の中に高さができるから、簡単に求めることができました。

私も同じ方法で求めました。すると、面積を求める式は６×８÷２＝24になるので、24㎠になります。

僕は、大きな三角形から小さな三角形を引く方法を考えました。まず、点Ａからまっすぐに引いた直線と辺ＢＣを伸ばした直線の交わったところを点Ｄとします。すると、大きな三角形ＡＢＤと小さな三角形ＡＣＤができます。三角形ＡＢＤは（６＋４）×８÷２＝40、三角形ＡＣＤは４×８÷２＝16になり、40－16＝24をして、24㎠になりました。

どちらもこれまで学習したことを使って求められていますね。ところで、みなさんはどの部分を高さと見ているのですか。

私はこの部分（赤線）です。

僕は辺ＡＤ（青線）です。

どちらも８㎝ですね。では、底辺を辺ＢＣとしたとき、その高さを公式に当てはめて三角形の面積を求めてもよいのでしょうか。

きちんと面積が求められているから、僕は大丈夫だと思います。

でも、高さが元の三角形からはみ出たり、外にあったりするのに、高さとして扱ってもいいのかな。

僕は同じ高さの三角形をいくつか描いて考えてみました。これまで学習した形の三角形①、②の点Ａに注目しました。すると、点Ａを通り、辺ＢＣに水平な直線を引くと、点Ａは上の直線上を動いているだけのように見えます。つまり、三角形の高さは、図形の外にあっても大丈夫だと言えます。

本当だ。どの三角形も６×８÷２の式で求められるね。形は違ってもどれも24㎠になるから、三角形の高さは図の中になくてもいいんだ。

ということは、高さが図形の外にあっても、三角形の面積を求める公式を使えることができるね。

四年生の学習で、｢平行な２本の直線の『幅』は、どこを測っても等しい」ことを学習しました。これを使うと、三角形の高さは、図形の中にも外にもとれることが分かりやすいですね。

学習のまとめ

三角形の面積は24㎠
６×８÷２＝24　　　　
底辺の長さ（青線）は６㎝
高さ（赤線）は８㎝

・三角形の高さは、図形の外にとることもできる。
・高さを図形の外にとっても、面積の公式を使って面積を求めることができる。

【四年生での学習】
平行な２本の直線の「幅」は、どこを測っても等しい。

評価問題

次の三角形の面積を求めましょう。

子供に期待する解答の具体例

５×４÷２＝10
答え　10㎠

本時の評価規準を達成した子供の具体の姿

図形の外にある高さを正しく見付け、三角形の面積を求める公式を使って面積を求めている。

感想例

高さが図形の中にないと面積を求めることができないと思っていたけど、高さが図形の外にある三角形の面積も計算できることが分かりました。
三角形の公式が当てはまらない三角形は絶対にないのか、いろいろと考えてみたけどありませんでした。どんな三角形であっても、公式を使って面積を求めることができるはずです。
底辺に平行な線を引いて考えると、三角形の高さについて納得することができました。
形が違う三角形は面積も違って見えるけど、底辺と高さに注目するとどれも同じ面積になっていて、不思議で面白いと思いました。
三角形の公式は、どんな三角形についても使えることができることに、すごいなと思いました。
面積を求めることのできる図形が増えてきました。もっと増やしていきたいです。
四年生で学習した「平行線の幅」という見方と三角形の「高さ」という見方は、とても関係が深いと思いました。
「高さ」は「頂点から底辺に垂直に下ろした線の長さ」だと考えていました。でも、「平行線の幅」という見方ができるようになりました。

ワークシート（ダウンロード可）

ダウンロードはこちら＞＞