小5算数「単位量あたりの大きさ」指導アイデア《単位量あたりの大きさで混み具合を比べる》
執筆/福岡教育大学附属小倉小学校教諭・楠木大二郎
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
単元の展開
第1時(本時)部屋の混み具合を調べ、単位量あたりの考え方について知る。
▼
第2時 日常生活のなかで単位量あたりの考え方が使われていることを知り、量の大きさを比べる。
▼
第3時 人口密度について知り、大きさを比べる。
本時のねらい
畳の枚数と子供の人数の関係に着目し、3つの部屋の混み具合を調べる活動を通して、一方の量にそろえる考えや、単位量あたりの大きさの考えで、混み具合を比べることができるようにする。
評価規準
畳の枚数と子供の人数のどちらか一方の量を単位量にそろえて、混み具合を比べることができる。(知識・技能)

修学旅行で宿はくする部屋には、ア、イ、ウの3つの部屋のタイプがあります。どの部屋が一番混んでいますか。 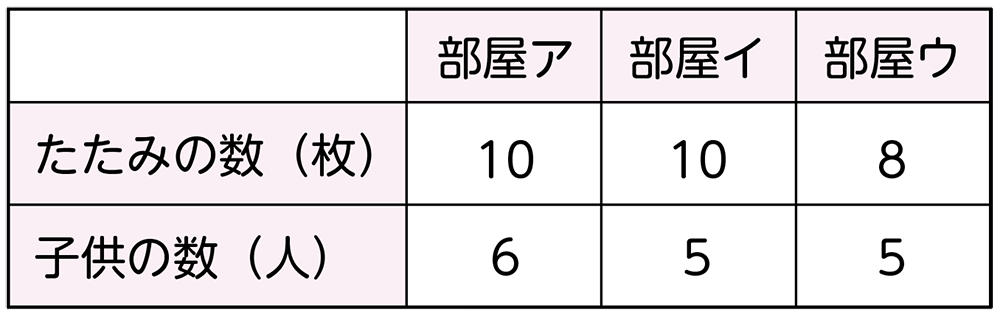
見通し
導入では畳の数と子供の数の表を提示し、どの部屋が一番混んでいるかを尋ねます。順に考えていくことで、子供たちは、最終的には畳の数と子供の人数がそろっていないアとウの部屋が、このままでは混み具合を比べることができないことに気付きます。
そこで、部屋アと部屋ウの図を提示し、畳の数か子供の数をそろえれば比べられそうであることを見通しながら、本時の学習のねらいを導き出します。
混み具合を比べられそうな部屋はどこですか。
アとイです。畳の枚数が同じだから、子供の人数が多いアの部屋のほうが混んでいます。
イとウも比べられます。子供の人数が同じだから、畳の枚数が少ないウの部屋のほうが混んでいます。
アとウは比べられません。畳の枚数も子供の人数も同じではないからです。
アの部屋とウの部屋の混み具合は、比べられませんか。
※図を提示する。
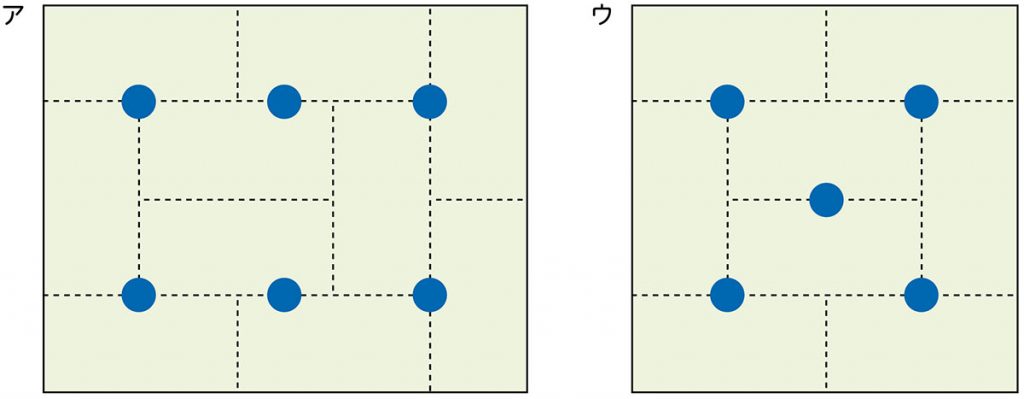
人数か畳の枚数をそろえれば、比べられそうです。

アとウの部屋では、どちらが混んでいるか考えよう。
自力解決の様子
A つまずいている子
ア 10―6=4
ウ 8―5=3
答え 部屋アのほうが混んでいる。
B 素朴に解いている子
・人数をそろえる考え
人数を30人にそろえます。
ア 10×5=50(枚)
ウ 8×6=48(枚)
答え 部屋ウのほうが混んでいる。
・枚数をそろえる考え
畳の数を40枚にそろえます。
ア 6×4=24(人)
ウ 5×5=25(人)
答え 部屋ウのほうが混んでいる。
C ねらい通り解いている子
・人数をそろえる考え
人数を1人にそろえます。
ア 10÷6=1.66・・・(枚)
ウ 8÷5=1.6(枚)
答え 部屋ウのほうが混んでいる。
・枚数をそろえる考え
畳の数を1枚にそろえます。
ア 6÷10=0.6(人)
ウ 5÷8=0.625(人)
答え 部屋ウのほうが混んでいる。
学び合いの計画
タブレットで友達の考えを共有できるICT環境が整備されている場合、自力解決の段階でノートに自分の考えをつくった子供に、その考えをタブレットで画像として保存し、提出させることで、クラス全体で共有できるようにします。
イラスト/横井智美