小4算数「変化と関係」指導アイデア《伴って変わる2つの数量の関係(差が一定)について、□や〇を使って式に表す》
執筆/東京都渋谷区立幡代小学校主任教諭・古澤和也
監修/東京都国立教育政策研究所教育課程調査官・加固希支男、東京都板橋区立上板橋小学校副校長・内藤信義
目次
年間指導計画
・大きい数
・折れ線グラフ
・角とその大きさ
・わり算1桁
・小数のしくみ
・垂直・平行と四角形
・わり算2桁
・およその数、計算の見積もり
・そろばん
・倍の見方
・資料の整理
・式と計算
・変わり方
・面積
・分数
・小数のかけ算とわり算
・直方体と立方体
単元の展開(各時の主な学習活動内容)
第1時 伴って変わる2つの数量の関係(和が一定)について、表を用いてその関係を捉え、□や〇を使って式に表す方法を考える。(□+〇=9)
第2時(本時)伴って変わる2つの数量の関係(差が一定)について、表を用いてその関係を捉え、□や〇を使って式に表す方法を考える。(□+2=〇)
第3時 伴って変わる2つの数量の関係(商が一定)について、表を用いてその関係を捉え、□や〇を使って式に表す方法を考える。(□×4=〇)
第4時 問題に取り組み、学習内容の定着を確認し、理解を確実にする。
本時のねらい
伴って変わる2つの数量の関係(差が一定)について、表を用いてその関係を捉え、□や〇を使って式に表す方法を考え、問題の解決に用いることができる。
評価規準
伴って変わる2つの量の関係(差が一定)について表を用いて変化や対応の特徴を調べ、□や○を使って式に表すことができる。
本時の教材のポイント
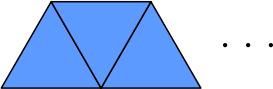
本時は下図のように1辺1㎝の正三角形を20個並べていった際の周りの長さを求めます。正三角形を20個かいて調べるのは大変であることから、伴って変わる2つの数量の関係に着目し、変化や対応の特徴を見いだすことで、20個並べた際の周りの長さを求めていく学習をします。まず、1辺1㎝の正三角形を1つずつ増やして提示することで、数量の変化に気付かせます。「正三角形の数が増える」「広さが変わる」「辺の数が変わる」「周りの長さが変わる」など、変化する数量について着目させた上で、本時の問題を提示します。
次に、正三角形20個並べたときの周りの長さを考える際に、正三角形の数が増えることで周りの長さも増えていることから、周りの長さと伴って変わっている正三角形の数に着目します。そして、前時の学習において伴って変わる2つの数量を考えた経験から、「正三角形の数」と「周りの長さ」という伴って変わる2つの数量の関係に着目し、変化や対応の特徴を見いだせば解決できるという見通しをもたせます。その際、以下の2点を意識させて解決に取り組ませることが大切です。
・正三角形1つのときは周りの長さは3㎝、正三角形2つのときは周りの長さは4㎝……と一方の数量を決めるともう一方の数量が決まるということ
・表に表すと、正三角形の数が変化するのに伴って、周りの長さがどのように変化するのか見いだせるということ
具体的には、「正三角形が3つで周りの長さは5㎝」「4つだと6㎝」「5つだと7㎝」と調べていく中で、「正三角形の数が1つ増えると周りの長さも1㎝増える(変化の様子)こと」や「いつも周りの長さは正三角形の数より2大きい(対応の特徴)こと」に気付くことで、これらの特徴を正三角形20個の際の周りの長さを求めることに用いていきます。
本時の展開
これは1辺1㎝の正三角形です。
※正三角形を1つずつ加えて見せる(図1)。

三角形が増えている。
2つになった。次は3つかな。
変化に気付いていますね。すばらしい。(正三角形を3つに増やす)
他に変化しているものはありますか。
正三角形、ひし形、台形と形が変わっています。
辺の数も増えていきます。
周りの長さも増えていきます。
今日の問題です。

1辺が1㎝の正三角形を20こならべたときにできる形の周りの長さは、何㎝でしょうか。
今は周りの長さは何㎝ですか(図2)。

5㎝です。
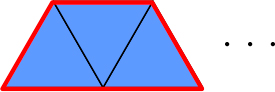
5㎝と答えた周りの長さは、この図のどの部分のことですか。指でなぞってみせてください。
(黒板などに提示された図をなぞりながら)ここです(図3)。
では、もう1個増やしてみましょう(図4)。
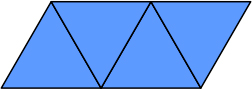
やはり周りの長さも増えました。
でも、これを20個かくのは大変です。
かかなくても求められる方法はないですかね。
前回は、2つの数を足すといつでも同じ答えになるという関係があったから、今回も2つの数の関係を見付けたら解けそうです。
正三角形の数と周りの長さは何か関係がありそうです。
三角形の数が増えると、周りの長さも増えるから何かきまりがありそう。
前の時間でやったように、正三角形の数と周りの長さにどのような関係があるかを調べると問題が解決できそうですね。

正三角形の数と周りの長さの関係を調べて、正三角形20個並べたときの周りの長さを求めよう。
見通し
どのようにして関係を調べますか。
ひとまず正三角形をいくつかかいてみます。
表をかいてみます。
この前のように式にも表してみたいです。
その後はどうしますか。
関係を□や○を使った式に表してみます。
- 実際に正三角形をいくつかかいて調べてみよう。
- 正三角形の数と周りの長さがどう変わっていくかを表に整理して、関係を調べてみよう。
- きまりを言葉の式、□や○を使った式に表して、計算で答えを求めてみよう。
- 正三角形の数を□、周りの長さを○としよう。
自力解決の様子
A つまずいている子
・正三角形の数と周りの長さの関係について正しく表に表すことができない。
・表から変化と対応の特徴を見いだすことができない。
B 素朴に解いている子
・正三角形の個数と周りの長さの関係について表に表して調べている。
・表を縦に見て、いつも正三角形の個数に2を足したら周りの長さになることに気付いている。
C ねらい通り解いている子
・正三角形の個数と周りの長さの関係について表を用いて調べ、表を横や縦に見て変化や対応の特徴に気付いている。
・見付けた関係を「正三角形の個数+2=周りの長さ」や、「□+2=〇」と式に表している。
・□に20を入れて計算し、周りの長さは22㎝と答えている。
全体発表とそれぞれの考えの関連付け
関係を調べるためどんなことをしましたか。
表に表しました。
表はこのようになりました。

正三角形3つまでは調べたけれど、そのあとはどうしたのですか。
実際にかいて確認しました。正三角形4個のときは周りの長さは6㎝で、5個なら7㎝でした。
ここから先は正三角形をかかなくてもいいと思いました。なぜなら正三角形の数が1個増えると周りの長さも1㎝増えるからです。
この表から何か発見があったのですね。
表を横に見ていったら、正三角形の数が1増えるごとに、周りの長さも1増えていました。
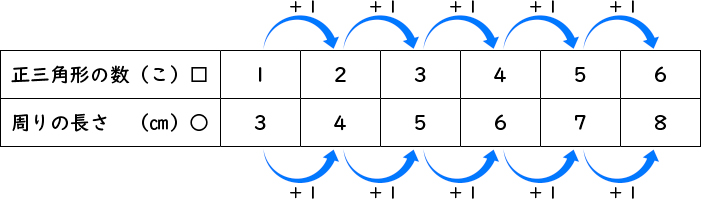
表を縦に見ていったら、正三角形の数に2を足すと周りの長さになっていました。

正三角形の数と周りの長さの関係が見えてきましたね。表以外の方法で関係を表してみた人はいますか。
言葉の式で表しました。「正三角形の数+2=周りの長さ」です。
「周りの長さ-正三角形の数=2」とも言えます。
正三角形の数を□、周りの長さを〇として□や○を使った式に表すと、「□+2=○」です。
この式はどのようにして思いついたのですか。
表を縦に見た関係を式に表しました。
正三角形の数が□でいつも+2をすると周りの長さの〇になっているからです。
言葉の式や□と〇の式に表したのですね。表にあるどの2つの数でもそうなっているか確認してみましょう。

確かに、三角形の数の□や周りの長さの〇に入る数が変わってもいつも同じ関係になっていますね。表や式に表すことで、この伴って変わる2つの数量の関係が見えてきました。ところで、今日は何を求める問題でしたか。
正三角形が20個のときの周りの長さです。
どうしたら求めることができますか。
正三角形の数に2を足すと周りの長さになるから22㎝です。
□+2=〇の□が正三角形の数なので、□に20を当てはめます。20+2=22となり、答えは22㎝です。
2つの数量に着目してその関係を調べていくと、計算で答えが求められましたね。
まとめ
- 正三角形の数と周りの長さの関係は、表を用いて調べたり、式に表したりすると分かりやすい。
- 数が大きくなってもその関係を式に表すことで知りたい数を計算で求めることができる。
評価問題
正三角形の数が20個のときの周りの長さは求められました。正三角形の数がもっと多くても周りの長さは求められますか。
□と〇の式を使えば求められます。
①正三角形の数が40このときの周りの長さは何㎝でしょうか。
②周りの長さが56㎝のときの正三角形の数はいくつになりますか。
子供に期待する解答の具体例
①40+2=42 答え42㎝
②56-2=54 答え54個
感想例
- 伴って変わる2つの数を表に整理すると、その関係が詳しく分かりました。
- 正三角形が20個並んだときのように数が大きいときも、□と〇の式に表すと全部調べなくても求めることができました。
- 前回は2つの数を足すといつでも同じ数になる問題でしたが、今回は2つの数を引くといつでも同じ数になる問題でした。他にもどのような関係があるか知りたいです。
ポイント&アドバイス
構成/桧貝卓哉 イラスト/横井智美 図版作成/永井俊彦

