小５算数「分数のたし算とひき算」指導アイデア《分母をそろえて計算することの意味を考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.09.29

年間指導計画

年間指導計画はこちらをクリック

・整数と小数
・体積
・合同な図形
・比例
・小数のかけ算
・平均
・単位量あたりの大きさ
・小数のわり算
・速さ
・図形の角
・整数の性質
・分数のたし算とひき算
・わり算と分数
・面積
・割合
・帯グラフと円グラフ
・円と正多角形
・□と△を使った式

単元の展開（各時の主な学習活動内容）

第１時（本時）異分母分数の加減計算について、単位分数に着目して、分母をそろえて計算することの意味を考える。
第２時　分数の性質を捉え、大きさの等しい分数の見付け方を考える。
第３時　分母の公倍数に着目し、「通分」のしかたを考え、分数の減法計算をする。
第４時　分母の公倍数に着目し、３つの分数の通分のしかたを考える。
第５時　分数の加法計算の和について、分母と分子の公約数に着目し、「約分」のしかたを考える。
第６時　前時の適用問題
第７時　分数の意味や表現に着目し、分数の加減計算のしかたをまとめる。
第８時　分数の意味や表現に着目し、帯分数の加減計算のしかたを考える。
第９時　分数の意味や表現に着目し、分数と小数の混じった加減計算のしかたを考える。
第10時 分数を用いた時間の表し方を考える。
第11時 学習内容の習熟・定着を図る。

本時のねらい

異分母分数の加減計算について、単位分数や同値分数に着目して、分母をそろえて計算することの意味を考え、説明する。

評価規準

異分母分数の加減計算について、単位分数や同値分数に着目しながら、分母をそろえて計算することの意味を考え、説明することができる。
異分母分数の加減計算は、分母をそろえると計算できることに気付き、同値分数を見付けようとしている。

本時の教材のポイント

ここでは、分母が違う分数同士の計算の仕方を考えていきます。通分をすることによって、分母が同じ分数の加法や減法として計算することができます。しかし、形式的に通分をして計算するだけでは、子供たちが「分数の意味や表現に着目し、計算の仕方を考えること」を身に付けるのは難しくなります。よって、同値分数（大きさの等しい分数）を見付けると、分母をそろえて計算ができ、単位分数のいくつ分で計算できることに気付くようにしていきます。

本時では、まず、具体の長さを示しやすく、分母をそろえやすい「[MATH]\(\frac{1}{2}\)[/MATH]ｍ」と「[MATH]\(\frac{1}{4}\)[/MATH]ｍ」の２つのテープを教材として提示します。それらのテープの長さを合わせた長さを考えていく際に、数直線の上にのせて分数を示すことや、単位分数（[MATH]\(\frac{1}{4}\)[/MATH]）のいくつ分に着目することなどを通して、分母をそろえて計算することの意味をつかむことができるようにします。その後の計算に、具体の長さでは示しにくい「[MATH]\(\frac{1}{3}\)[/MATH]ｍ」が入ってきても、同じように分母をそろえて計算するために同値分数を見付け、それを用いて計算の仕方を説明することができるようにしていきます。最後に、異分母分数のたし算で身に付けたことが、異分母分数のひき算でも適用できるか確かめるための問題についても考えていきます。

本時の展開

ここに紙テープが２つあるのですが、それぞれ何ｍだと思いますか。

70cmと20cm。

１ｍ！

10cmと30cm。

答えは[MATH]\(\frac{1}{2}\)[/MATH]ｍと[MATH]\(\frac{1}{4}\)[/MATH]ｍですよ。

分数はずるいよ。

「何ｍ」と聞いたのですが、cmで答えた人もいたね。ちなみ[MATH]\(\frac{1}{2}\)[/MATH]ｍと[MATH]\(\frac{1}{4}\)[/MATH]ｍは何㎝になりますか。

[MATH]\(\frac{1}{2}\)[/MATH]ｍは50cm。

[MATH]\(\frac{1}{4}\)[/MATH]ｍは25cmだよ。

合わせると何cmになりますか。

75cm。

どんな式になるでしょうか。

50＋25＝75。

では、それらと同じ長さの[MATH]\(\frac{1}{2}\)[/MATH]ｍと[MATH]\(\frac{1}{4}\)[/MATH]ｍを合わせると、式はどうなりますか。

[MATH]\(\frac{1}{2}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]

えっ。

なぜ、えっと驚いたんですか。

分母が違うからたし算できません。

分母が同じだったらすぐ分かるのに。

分母を同じにしたらいいんだよ。

そんなことができるんですか。

できます。

そんなことしたら、大きさが変わってしまいそうな気がしますが……。では、みんなで考えていきましょうか。

[MATH]\(\frac{1}{2}\)[/MATH]ｍのテープと[MATH]\(\frac{1}{4}\)[/MATH]ｍのテープがあります。合わせると何ｍになりますか。

分数の大きさを変えずに、分母の数を同じにできないか考えよう。

計算の仕方を考えたり説明したりするときに、よく使っていたものは何でしたか。

式を使っていました。

図で考えました。

図や式を使ってきたのですね。では、まず図に表してみますね。

この図を見てもよく分からないなあ。

それでは、テープを動かして、合わせてみましょうか。

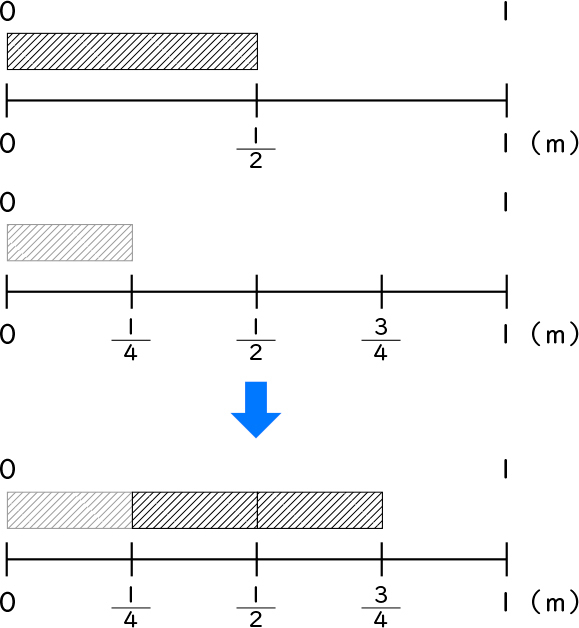
合わせてみましたが、どうですか。

あっ、[MATH]\(\frac{3}{4}\)[/MATH]ｍにぴったりだよ。

[MATH]\(\frac{1}{4}\)[/MATH]ｍのテープが３つあるように見える。

実際に[MATH]\(\frac{1}{4}\)[/MATH]ｍのテープを[MATH]\(\frac{1}{2}\)[/MATH]ｍのテープに重ねてみましょうか。

[MATH]\(\frac{1}{2}\)[/MATH]ｍのテープは、[MATH]\(\frac{1}{4}\)[/MATH]ｍのテープの２つ分だ。

だって、２年生のときに[MATH]\(\frac{1}{2}\)[/MATH]からさらに半分にしたら[MATH]\(\frac{1}{4}\)[/MATH]になったから当たり前だよ。

では、[MATH]\(\frac{1}{2}\)[/MATH]ｍのテープは、[MATH]\(\frac{1}{4}\)[/MATH]ｍのテープの２つ分だということが分かりましたね。

分数の大きさを変えずに、分母の数を同じにできないか考えていたよね。

図を見たら、[MATH]\(\frac{1}{2}\)[/MATH]ｍと[MATH]\(\frac{2}{4}\)[/MATH]ｍは等しい大きさだから、[MATH]\(\frac{1}{2}\)[/MATH]ｍは[MATH]\(\frac{2}{4}\)[/MATH]ｍに変えてもいいんじゃない。

４年生のときにも、等しい大きさの分数を見付けたな。[MATH]\(\frac{1}{2}\)[/MATH]ｍと[MATH]\(\frac{2}{4}\)[/MATH]ｍは等しい大きさだったよ。

[MATH]\(\frac{1}{2}\)[/MATH]ｍを[MATH]\(\frac{2}{4}\)[/MATH]ｍに変えても、大きさは変わらないということですね。それを式にしたらどうなるかな。

[MATH]\(\frac{2}{4}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]になります。

それなら計算できる！

[MATH]\(\frac{2}{4}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]＝[MATH]\(\frac{3}{4}\)[/MATH]だよ。

分母を同じにできて、それで計算もできましたね。どうして[MATH]\(\frac{2}{4}\)[/MATH]＋[MATH]\(\frac{1}{4}\)[/MATH]＝[MATH]\(\frac{3}{4}\)[/MATH]になるのですか。

[MATH]\(\frac{1}{4}\)[/MATH]を基にすると、[MATH]\(\frac{1}{4}\)[/MATH]の２つ分と１つ分だから、合わせて[MATH]\(\frac{1}{4}\)[/MATH]の３つ分で[MATH]\(\frac{3}{4}\)[/MATH]になります。

図を見ても、[MATH]\(\frac{1}{4}\)[/MATH]ｍの３つ分になっているね。

[MATH]\(\frac{1}{4}\)[/MATH]を基にして考えると、整数のたし算で計算できるんだったね。

そうそう、だからすぐにできる。

[MATH]\(\frac{1}{2}\)[/MATH]ｍのテープと[MATH]\(\frac{1}{3}\)[/MATH]ｍのテープがあります。合わせると何ｍになりますか。

この問題も、「大きさを変えずに、分母を同じ数にする」ことはできますか。

できるのかな。

できるよ！

さっきみたいに、図があったら分かるかも。

４年生のときに使った図はありますよ。これがあれば考えられますか。

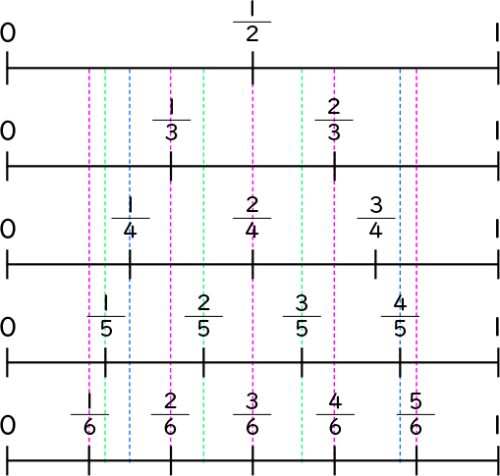
できそう

それでも不安だな。

では、考えてみましょう。図は「１人１台端末」に送りますので、それを使って考えを書き込んでください。分からない人は先生や友達に相談しましょう。

見通し

数直線の中にテープ図をかいて、等しい大きさの分数を探そう。

図を見て、[MATH]\(\frac{1}{3}\)[/MATH]と等しい大きさの分数を見付けよう。

分母の２と３で、大きさが変わらないところを見て、同じ分母の数を探そう。

自力解決の様子

Ａ　つまずいている子

・等しい大きさの分数を見付けられず、教師の支援を待っている。

・等しい大きさの分数は見付けたが、分母を同じ数にそろえることができていない。

Ｂ　素朴に解いている子

・等しい大きさの分数を見付け、分母を同じ数にそろえることができている。

・等しい大きさの分数を見付けているが、計算の解は出せていない。

Ｃ　ねらい通りに解いている子

・等しい大きさの分数を見付け、分母を同じ数にそろえることができ、計算の仕方についても考えている。

・図を見なくても、４年生の同値分数の学習を活用して、分母を同じ数にそろえることができ、計算についても考えている。

全体発表とそれぞれの考えの関連付け

Ａさんはどのように考えたのですか。

Ａさん　[MATH]\(\frac{1}{3}\)[/MATH]ｍと等しい大きさの分数を見付けようとして、図の[MATH]\(\frac{1}{3}\)[/MATH]と等しい大きさのところを探しました。そうすると、[MATH]\(\frac{1}{3}\)[/MATH]と[MATH]\(\frac{2}{6}\)[/MATH]が等しい大きさだと分かりました。

Ａさんは[MATH]\(\frac{1}{3}\)[/MATH]が[MATH]\(\frac{2}{6}\)[/MATH]と等しい大きさだと分かっていたけれど、私は、[MATH]\(\frac{1}{2}\)[/MATH]が[MATH]\(\frac{2}{4}\)[/MATH]や[MATH]\(\frac{3}{6}\)[/MATH]と等しい大きさだと分かりました。

２人が言っていたけど、[MATH]\(\frac{1}{3}\)[/MATH]が[MATH]\(\frac{2}{6}\)[/MATH]と等しい大きさで、[MATH]\(\frac{1}{2}\)[/MATH]が[MATH]\(\frac{3}{6}\)[/MATH]と等しい大きさだから、[MATH]\(\frac{1}{3}\)[/MATH]＋[MATH]\(\frac{1}{2}\)[/MATH]は[MATH]\(\frac{2}{6}\)[/MATH]＋[MATH]\(\frac{3}{6}\)[/MATH]と同じになります。[MATH]\(\frac{2}{6}\)[/MATH]＋[MATH]\(\frac{3}{6}\)[/MATH]＝[MATH]\(\frac{5}{6}\)[/MATH]なので、答えは[MATH]\(\frac{5}{6}\)[/MATH]ｍになります。

どうして、[MATH]\(\frac{2}{6}\)[/MATH]＋[MATH]\(\frac{3}{6}\)[/MATH]＝[MATH]\(\frac{5}{6}\)[/MATH]になるのでしたか。

[MATH]\(\frac{2}{6}\)[/MATH]は[MATH]\(\frac{1}{6}\)[/MATH]の２つ分で、[MATH]\(\frac{3}{6}\)[/MATH]は[MATH]\(\frac{1}{6}\)[/MATH]の３つ分だから、[MATH]\(\frac{1}{6}\)[/MATH]の２つ分と３つ分を合わせて、[MATH]\(\frac{1}{6}\)[/MATH]の５つ分。[MATH]\(\frac{1}{6}\)[/MATH]の５つ分は[MATH]\(\frac{5}{6}\)[/MATH]になるので、[MATH]\(\frac{5}{6}\)[/MATH]ｍです。

[MATH]\(\frac{1}{4}\)[/MATH]を基にして考えるといいとさっき言ってたから、今回は[MATH]\(\frac{1}{6}\)[/MATH]を基にして考えるといい。

分母の違う分数どうしのたし算は、どうしたらよいかまとめますね。

分母を同じ数にそろえたらいい。

図を見て、等しい大きさにしないといけないよ

[MATH]\(\frac{1}{6}\)[/MATH]のいくつ分で考えて、整数のたし算にする。

では、ひき算でも同じようにできるか、やってみますか。

できるできる。

同じ大きさのまま、分母をそろえたらできるよ。

この問題を、先ほどと同じように図を使って考えてみましょう。

評価問題

[MATH]\(\frac{2}{3}\)[/MATH]Ｌのジュースがあります。そのジュースのうち[MATH]\(\frac{1}{2}\)[/MATH]Ｌ飲みました。残りは何Ｌになりますか。

子供に期待する解答の具体例

式　　[MATH]\(\frac{2}{3}\)[/MATH]－[MATH]\(\frac{1}{2}\)[/MATH]＝[MATH]\(\frac{4}{6}\)[/MATH]－[MATH]\(\frac{3}{6}\)[/MATH]＝[MATH]\(\frac{1}{6}\)[/MATH]

答え　[MATH]\(\frac{1}{6}\)[/MATH]Ｌ