小４算数「式と計算」指導アイデア《２位数÷２位数の筆算で、過大商を立てたときの仮商修正の仕方を理解し、計算する》
執筆／東京都荒川区立第七峡田小学校主幹教諭・山田篤
監修／東京都国立教育政策研究所教育課程調査官・加固希支男、東京都板橋区立上板橋小学校副校長・内藤信義
目次
年間指導計画
・大きい数
・折れ線グラフ
・角とその大きさ
・わり算１桁
・小数のしくみ
・垂直平行四辺形
・わり算２桁
・およその数、計算の見積もり
・そろばん
・倍の見方
・資料の整理
・式と計算
・変わり方
・面積
・分数
・小数のかけ算とわり算
・直方体と立方体
単元の展開（各時の主な学習活動内容）
第１時 数量の関係に着目し、式を読み取ったり、場面を１つの式に表したりする。
第２時 四則混合の式の表し方と、二段階構造の計算の順序について知る。
第３時 三段階構造の四則混合や（ ）のある式の計算の順序を整理する。
第４時 ドットの並び方やまとまりに着目し、ドットの数の求め方を考え、１つの式に表す。
第５時 数や式の形に着目し、分配法則をまとめ、それを用いて計算を工夫する。
第６時 式にある数に着目し、交換・結合法則をまとめ、それを用いて計算を工夫する。
第７時（本時）被乗数や乗数と積に着目し、乗法の性質を理解する。
第８時 学習した内容についてふり返り、見方や考え方の深まりについて確かめる。
本時のねらい
被乗数や乗数と積に着目し、乗法の性質を理解する。
評価規準
乗数を10倍すると積も10倍になり、被乗数と乗数をそれぞれ10倍すると積は100倍になるという乗法の性質を理解する。
本時の教材のポイント
本時では、「乗数を10倍すると積は10倍、被乗数と乗数をそれぞれ10倍すると積は100倍になる」という乗法の性質を学習します。この性質は第３学年の２桁のかけ算の学習で扱っていますが、交換法則や分配法則を学習したこのタイミングで学習することで、その根拠をより明確にする機会となります。この乗法の性質は、小数や分数のかけ算の学習で活用するとても大切な考え方となります。
導入では、まず８×３＝24という式を基に、８×30、80×30の積について考えていきます。子供は既習経験から
・10倍、100倍すると、位が１つ、２つ上がる。（大きな数の学習）
・掛ける数を10倍すると、積も10倍になる。（×何十のかけ算の学習）
ということを理解しているので、これらの知識を使って子供は容易に答えを求めることができると考えられます。その際、「８×３をして０をつける」というような素朴な言葉を基に、０を付けて位が上がることと10倍とを関連付け、既習内容を想起させます。
自力解決では、そこからさらに式同士の関係に着目していきます。８×３＝24という式を基にして８×30や80×30の式の中から10倍、100倍になる部分を見付けたり、既習の交換法則や結合法則を活用して計算の仕方を工夫したりします。しかし、式同士の関係を考えるとなると、何をしたらよいのか分からない子供がいることが予想されます。そこで、自力解決の場面でヒントカードを示すことで、もとの式と８×30や80×30の式との10倍・100倍の関係や、結合法則や交換法則を用いた式変形に気付くことができるようにします。
本時の展開
前の時間に、いろいろな計算のきまりについて学習しました。どんなきまりをやりましたか。
結合のきまりです。
交換のきまりもやりました。
そうですね。では、この積は分かりますか。
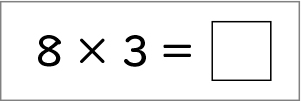
８×３＝24だ。
そうですね、24です。今日はこの式を基にして他の計算を考えてほしいのです。
８×３＝24をもとにして、積を求めよう。
８×３＝24を基にすると、次の積はどうなりますか。
簡単に出せます。
筆算しなくても計算できるね。
どのように積を求めるのですか。
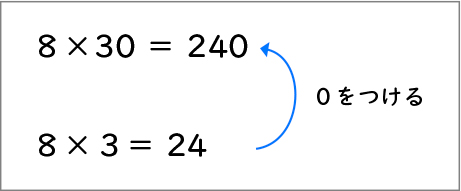
①の式は、８×３をして30の０の分、その答えの24に０をつければいいので240です。
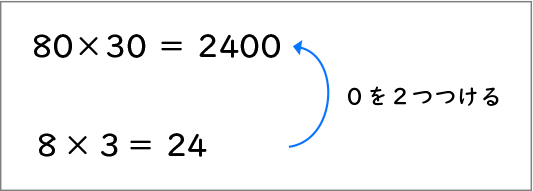
②の式は、80×30の両方の０の分、24に０を２つつければいいから2400です。
24に０をつけるとは、どういうことですか。
10倍すると位が１つ上がるので、０を１つつけることになります。
①は３年生のときにやりました。３のところが30になっているのは10倍していることと同じなので、積も同じように10倍すればいいから240です。
０を２つつけると位が２つあがるので100倍です。
２つの式の積を求めることができました。２つの式で共通しているのは、８×３＝24を基にして10倍や100倍しているところです。今日はどうしてそのように考えられるのか関係を探ってみたいと思います。
８×３＝24と２つの式の関係を調べよう。
見通し
どうやって関係を調べたらよいでしょうか。
２つの式を並べて書いて、０をとるやつけるなどではなく10倍とか使って書いてみます。
30は３×10と考えて、昨日やった交換のきまりや結合のきまりを使って工夫して考えてみます。
８×３＝24で８×30＝240だけど、どうやって比べたらいいのかな。
８×30＝240は８×３＝24の３が10倍になっていて、24も10倍になっているから……。
８×30＝８×（３×10）だから結合のきまりを使って……。
■自力解決に向けて提示するヒントカード
子供の実態に応じて、２つの式の倍の関係や結合のきまりや交換のきまりを使った式変形に気付けるような下記のヒントカードを示す。
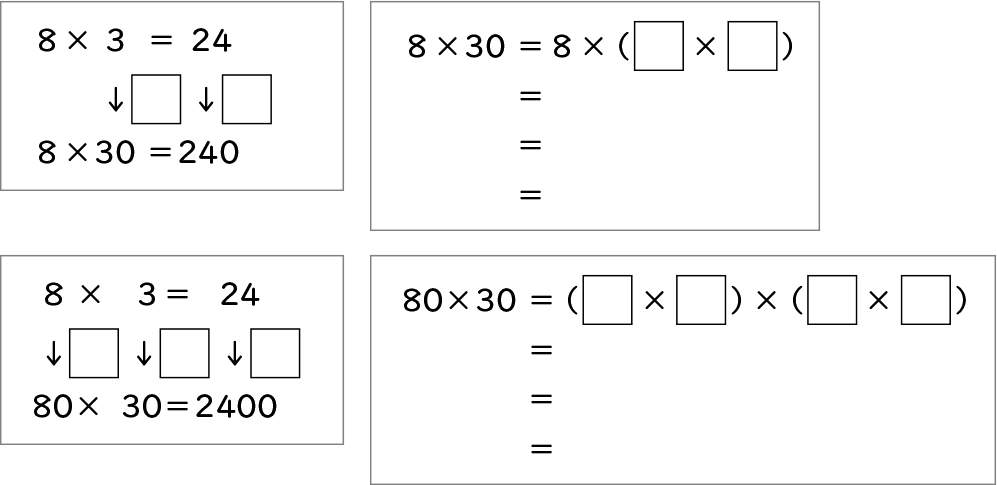
自力解決の様子
Ａ つまずいている子
・乗数の10倍と積の10倍の関係に気付くことができない。
８×３＝24
８×30＝240
Ｂ 素朴に解いている子
・乗数が10倍になると、積も10倍になることを説明している。
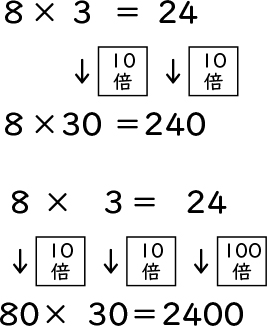
Ｃ ねらい通りに解いている子
・結合や交換のきまりを活用して式を変形させて考えている。
８×30＝８×（３×10）
＝（８×３）×10
＝24×10
＝240
80×30＝８×10×３×10
＝８×３×10×10
＝24×100
＝2400
ノート例
Ａ つまずいている子
※自分の考えの部分はヒントカードを渡している。
Ｃ ねらい通りに解決している子
※結合法則や交換法則を用いた式変形をしている。
全体発表とそれぞれの考えの関連付け
それぞれの式を見て、気付いたことはありますか。
８×３＝24と８×30＝240の２つの式を並べてみました。３が10倍になっていると24も同じように10倍になっています。
このきまりは、３年生のときにもやりました。
８×３＝24と80×30＝2400で並べてみたら、同じように10倍と10倍で2400のところは100倍になっています。
10倍が２つあると、答えは何倍になっていますか。
10×10＝100だから100倍になっています。
他の考え方はありますか。
８×30＝24の式は、３が10倍になっているから、それを昨日やった「結合のきまり」を使えば、（８×３）×10と考えられます。８×３＝24なので24×10になります。
80×30のほうはどうでしょうか。
今度は、80と30だから、30のほうはさっきと同じように３×10にすればいいから……。
同じように80も８×10にできると思います。
式にしたら、80×30＝８×10×３×10になります。
このあとどうすればよさそうですか。
交換のきまりを使って、順番を入れ替えたらいいと思います。
交換のきまりを使ったら、８×10×３×10の10と３を入れ替えられます。式は、８×３×10×10にできます。
×10が２つあるから×100にできるので、24×100になります。
×100が出てきたね。
つまり、何倍になっていると言えますか。
100倍になっています。
式の関係が見えてきましたね。きまりを使って式を工夫した考えがありましたが、これを見て、何か気付いたことはありますか。
初めに８×３をして24に０をつけると言っていたのが、この式の８×３を先に計算をして×10しているのと近いと思いました。
０を２つつけると言っていたところは、８×３を先に計算して24×100しています。
８×３＝24と２つの式の関係をかけ算の言葉を使ってまとめてみましょう。
掛ける数が10倍になると、積が10倍になります。
掛ける数と掛けられる数が10倍になると、積が100倍になっています。
学習のまとめ
- かける数が10倍になると、積も10倍になる。
- かけられる数とかける数がそれぞれ10倍になると、積は100倍になる。
かけ算のきまりを見つけることができましたね。このきまりは10倍以外の数でも成り立つと思いますか。
同じだけ倍すればいいからできると思います。
今日の学習をふり返って、やってみてください。
掛ける数が何倍になっているか考えてみて、答えを求めましょう。
３が15になっているから５倍になっています。
掛けられる数が５倍だから、積も５倍になるはずなので24×５＝120になります。
８×15は筆算すると120だからきまりは成り立ちます。
他の数になっても、このかけ算のきまりは成り立ちますね。
評価問題
５×６＝30をもとにして、次のかけ算の積を求めましょう。
①５×60
②50×60
③５×600
感想例
学習感想を書きましょう。今日、分かったことや、次に生かせそうなことなどを書きましょう。
式のほうが10倍になっていたら、それと同じように答えも10倍になっていた。
かけ算を全部計算しなくても、きまりを使えば計算がしやすくなる。
今日やったかけ算のきまりが、わり算ならどうなるのかやってみたい。
ポイント＆アドバイス
構成／桧貝卓哉 イラスト／横井智美 図版作成／永井俊彦