小３算数「かけ算の筆算１けた」指導アイデア《何十、何百×１位数の計算》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.09.29

年間指導計画

年間指導計画はこちらをクリック

・かけ算
・時刻と時間
・わり算
・たし算とひき算の筆算
・棒グラフと表
・余りのあるわり算
・長さ
・暗算
・かけ算の筆算　１けた
・１万を超える数
・円と球
・重さ
・わり算や分数
・何倍でしょう
・小数
・分数
・三角形と角
・計算の順序
・式と計算
・かけ算の筆算　２けた
・そろばん

単元の展開（各時の主な学習活動内容）

第１時（本時）何十、何百×１位数の計算
第２時　被乗数と積の関係の考察
第３時　２位数×１位数の計算
第４〜７時　２位数×１位数の筆算
第８・９時　３位数×１位数の筆算
第10時　乗法の結合法則
第11時　まとめ

本時のねらい

何十、何百×１位数の計算を10や100を単位として考え、そのいくつ分と見ることで、乗法九九などの基本的な計算を基にしてできることを理解し、説明する。

評価規準

何十、何百×１位数の計算を10や100のまとまりや既習の乗法九九に着目して計算する方法を考え、説明することができる。

本時の教材のポイント

何十、何百×１位数の計算の仕方を考える際には、単位数の何個分に着目して数を相対的に捉えることが重要になります。そのため、10や100を単位として考えるためにも、10円玉や100円玉をイメージできる買い物の場面を問題として取り扱います。

問題場面では被除数にあたる数を□にして条件不足の問題（問題文：１個□円のチョコレートが３個あります。代金はいくらですか）として提示します。「１個20円だったら？」「１個200円だったら？」と、値段を変えて展開していきます。その解決過程で、子供から「掛けられる数が20や200（何十も何百）のかけ算は、10のまとまりや100のまとまりで考える」ことで、どちらもこれまで学習した「２×３」の乗法九九を活用していることに気付くことができるようにします。

本時の授業では、問題場面から立式し、答えを求めることにあまり困難さはないと考えます。ただ、子供が求めた答えが、本時のねらいである10や100を単位として求めているのかを把握するのは困難です。もしかすると、同数累加をして答えを求めていたり、「０をとって２×３＝６、６に０を戻して60になる」というような機械的な計算処理で求めていたりしているかもしれません。そこで、本時では、立式した問題をどのように解決できたのかを説明する時間を大切にしていきます。

また、10や100をまとまりとして捉えることによって、既習の乗法九九を活用していることに気付かせていきます。そのため、20×３と200×３の計算の仕方の考えを並列して板書するように工夫します。そのような板書により、子供から「もっと大きな数（2000円）にしたらどうなるのだろう？」という発展的に考察する発言や、「２×〇と20×〇と200×〇には何かきまりがありそう」など、次時の学習（被乗数と積の関係の考察）につながる発言が出てくることが考えられます。

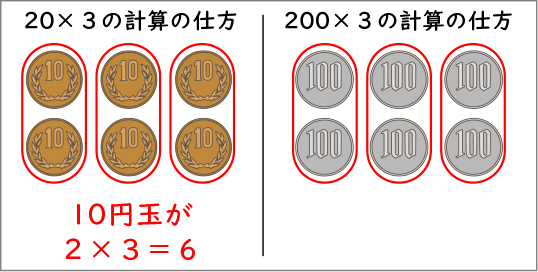
本時の問題を同数累加で求める子供もいることが予想されます。そのような考えも認めた上で、10や100を単位として考えることで、乗法九九によって答えが求められるよさにも気付かせていきます。そのため、10や100を単位として考えることが困難な子供には、図１のようなシートをデジタル上で配り、１人１台端末を活用します（赤色の字や囲みが子供の記述例）。このようにすることで、模擬貨幣を実際に活用するよりも、子供の机上が整理されたり、その子なりの説明の記述が残ったりするメリットがあります。

本時の展開

みんなはお店に行って、１つの商品をたくさん買ったことはありますか。

あります。

そのとき、自分で「いくら払えばいいかな」と代金を考えたことがありますか。

あります。でも、１個とか２個買うだけで、たくさんのものを買ったことはありません。

ないかもしれません。

今日は、そのようなお買い物の場面の問題です。

１こ□円のチョコレートを３こ買います。
代金はいくらですか。

チョコレートの１個の値段が分からないと求められません。

では、１個20円のチョコレートの場合の代金はいくらですか。式とその理由も書いてみましょう。

１つ分が20円で、その３つ分だから、20×３になります。

例えば、５円のものを２つ買ったら、５×２＝10で10円になりました。だから、この場合は、20×３になります。言葉の式だと『１個の値段×買う数＝代金』になります。

１個200円の場合だったら、どのような式になりますか。

値段の高いチョコレートですね。その場合、200×３の式になります。理由は20×３と同じです。

課題をつかむ

この20×３と200×３の計算は、これまでのかけ算の学習と何が違いますか。

掛けられる数が大きいことがこれまでの学習と違います。

掛けられる数や掛ける数が10のときのかけ算は学習しましたが、それ以上の何十や何百の計算はしていません。

掛けられる数が10を超えた大きな数でも、12×３の12までしか学習していません。

それでは、今日の学習は何を考えていきますか。

20×３と200×３の計算の仕方を考えます。

答えだけではなくて、その説明もノートに書きましょう。

20×３と200×３の計算の仕方を考えよう。

見通し

20が３個だから、たし算で考えられる。でも、掛ける数が大きくなると大変になるなあ。

お金の図で考えてみたり、言葉で説明したりしてみよう。

20は10が２個分だから、10円玉で考えると２個。それが３つ分あるから……。

自力解決の様子

Ａ　つまずいている子

・20×３＝60、200×３＝600の計算は、20＋20＋20、200＋200＋200ということは理解できるが、10や100のまとまりに着目して計算する方法を説明できない。

Ｂ　素朴に解いている子

・20×３＝60、200×３＝600の計算は、20＋20＋20、200＋200＋200ということを理解できている。

・図や言葉を使って、10や100のまとまりに着目して説明できている。

Ｃ　ねらい通りに解いている子

・図や言葉を使って、10や100のまとまりに着目して、20×３、200×３のどちらも既習の乗法九九（２×３）が使われていることを説明できている。

ノート例

Ａ　つまずいている子

※同数累加は理解できるが、単位の考えに着目できていない（ノート左下）

※つまずいている子には、先述の図１にある１人１台端末を活用する

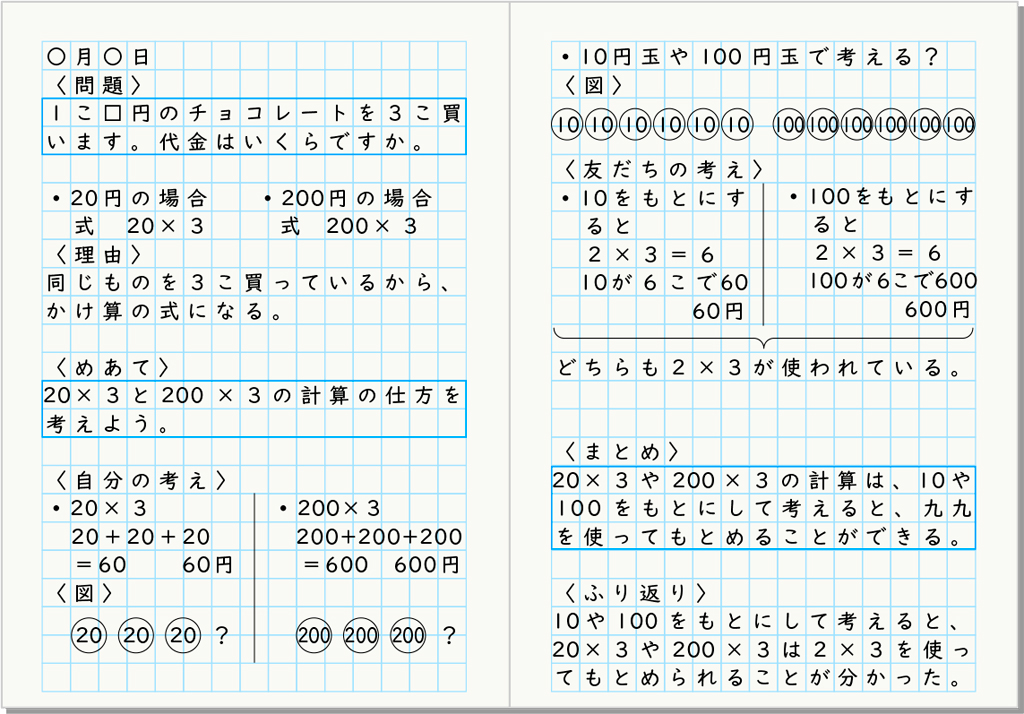
Ｂ　素朴に考えている子

※10や100の単位の考えに着目できている（ノート左下）

Ｃ　ねらい通りに解いている子

※10や100の単位の考えに着目し、乗法九九（２×３）が使われていることを説明できている

全体発表とそれぞれの考えの関連付け

それでは３人の子に発表してもらいます。どのように考えましたか。

（Ａさん）　20×３は、20が３つ分だから、20＋20＋20＝60で、60円と計算しました。同じように、200×３は、200が３つだから、200＋200＋200＝600で、600円としました。

（Ｂさん）　私は図で考えました。

（Ｃさん）　私はＢさんと似ていて、お金の図をかきました。

３人の考えはどうですか。

どれも60円と600円で答えが同じで、どの考えもいいと思います。

そうですね。みんな60円と600円で答えは同じになりましたね。

でも、Ａさんの考えだと、３個分の代金ならいいですが、もし買う数がどんどん多くなると、たし算で考えていくのは大変です。

２年生のときも、足していくのが大変だから、１つ分×いくつ分で求められる「かけ算九九」を学びました。

よく覚えていますね。では、みなさんが出してくれた考えの中に、これまでに学習した「かけ算九九」が使われていますか。

Ｃさんの考えに２×３の九九が使われています。

そうですね。他にも答え以外にも似ているところや同じところはありますか。

ＢさんもＣさんも10や100のまとまりの数で考えています。

Ｄさん　Ｂさんの図もＣさんと同じで「10が６個」「100が６個」と書いてあるから、それも「10が２×３で６個」「100が２×３で６個」と同じことだと思います。

どういうことか分からないです。

Ｄさんは、どうやって、ＢさんとＣさんの図から「２×３」を見付けたのですか。

Ｄさん　だって、どっちの図（Ｂさんの図・Ｃさんの図）も丸の数だと２×３になるから……。

※教師がＤさんの考えを図で表す（図の活用）

分かった。そういうことか。

本当だ。20×３も200×３も、計算の仕方に「２×３」の九九が見付けられた。

じゃあ、20×３も200×３も、10や100のまとまりで見たら、これまでに学習した「かけ算九九」で求められるね。

なるほど、20×３や200×３の計算の仕方は、初めての学習でしたが、10や100のまとまりに注目して考えると、これまで学習したかけ算九九で求めることができましたね。

１個500円のチョコレートとか大きな数でも、同じ考えで求めることができそう。

学習のまとめ

20×３や200×３の計算は、10や100を基にして考えると、九九を使って求めることができる。

評価問題

①60×４、600×４の計算の仕方をせつ明しましょう。

②次の計算をしましょう。
（１）80×７
（２）500×５

子供に期待する解答の具体例

① 60×４は、10が６×４で、24個だから、240。
　 600×４は、100が６×４で、24個だから、2400。

② （１）80×７＝560
　（２）500×５＝2500

感想例

何十や何百×１桁の計算は10や100を基にして考えれば、これまで学習したかけ算九九を使って求められることが分かった。
１個2000円のチョコレートでも、1000を基にして考えれば、2000×３もかけ算九九を使って求めることができるかもしれない。
20×３＝60で、200×３＝600で、２×３＝６だから、縦にならべてみると、
　２×３＝６
　 20×３＝60
　200×３＝600
となって、掛けられる数が10倍すると、答えも10倍になるというきまりがあるかもしれない。他の数でも調べてみたい。